剑指:数值的整数次方
Posted lisen10
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了剑指:数值的整数次方相关的知识,希望对你有一定的参考价值。
题目描述
实现函数 double Power(double base, int exponent),求 base 的 exponent 次方。
不得使用库函数,同时不需要考虑大数问题。
注意:
- 不会出现底数和指数同为 0 的情况。
- 注意判断值数是否小于 0。另外 0 的 0 次方没有意义,也需要考虑一下,看具体题目要求。
样例1
输入:10 ,2
输出:100
样例2
输入:10 ,-2
输出:0.01
解法
解法一
public static double power(double base, int exponent) if(exponent==0) return 1; if(exponent==1) return base; double res = 1; for(int i=0;i<Math.abs(exponent);i++) res *= base; return exponent > 0 ? res : 1/res; public static void main(String[] args) System.out.println(power(2,-3)); //0.125
时间复杂度:O(n)
解法二
思想:如果输入指数exponent为32,那么可以在它16次方的基础上平方即可;而16次方是8次方的平方。依次类推,求32次方只需做5次乘法:a2,a4,a8,a16,a32
求a的n次法,公式
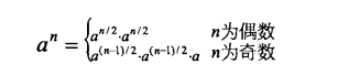
递归求解,每次 exponent 缩小一半,时间复杂度为 O(log N)。
public class Solution public static double power(double base, int exponent) if(exponent==0) return 1; if(exponent==1) return base; double res = power(base, Math.abs(exponent)>>1); res *= res; //平方 if((exponent & 1) == 1)//指数为奇数时 res *= base; return exponent > 0 ? res : 1/res; public static void main(String[] args) System.out.println(power(3,7)); //2187
7 3 1
以上是关于剑指:数值的整数次方的主要内容,如果未能解决你的问题,请参考以下文章