BZOJ 1969: [Ahoi2005]LANE 航线规划( 树链剖分 )

Posted 2020-06-13

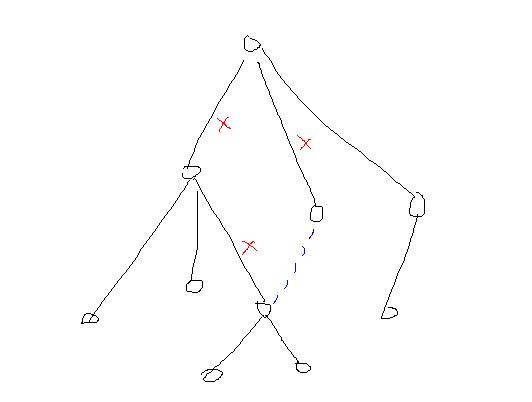
首先我们要时光倒流, 倒着做, 变成加边操作维护关键边. 先随意搞出一颗树, 树上每条边都是关键边(因为是树, 去掉就不连通了)....然后加边(u, v)时, 路径(u, v)上的所有边都变成非关键边了, 因为形成了环, 环上任意2点有2条路径。。。下图, 加上蓝色的边, 红色x的边就变成了非关键边.

  

所以树链剖分维护一下...时间复杂度O(NlogN+MlogM+Qlog^2N), 可以AC.

翻了翻ZY的标解:“动态维护树+最近公共祖先查询”....复杂度是O(NlogN+M+QlogN)的.比我不知道高到那里去.....不过他的解法太神了orz(其实是懒得看= =

----------------------------------------------------------------------------------------

#include<cstdio>

#include<cctype>

#include<cstring>

#include<algorithm>

 

using namespace std;

 

typedef pair<int, int> pii;

 

const int maxn = 30009;

const int maxM = 100009;

const int maxQ = 40009;

 

int par[maxn], F[maxM], ans[maxQ];

int M, N, qn, n, L, R;

int fa[maxn], ch[maxn], top[maxn], sz[maxn], dep[maxn], Id[maxn], TOP;

 

inline int getint() {

char c = getchar();

for(; !isdigit(c); c = getchar())

if(c == ‘-‘) return  -1;

int ret = 0;

for(; isdigit(c); c = getchar())

ret = ret * 10 + c - ‘0‘;

return ret;

}

 

struct Q {

int t, u, v;

} q[maxQ];

 

struct E {

int u, v;

E() {}

E(int _u, int _v) : u(_u), v(_v) {

}

bool operator < (const E &p) const {

return u < p.u || (u == p.u && v < p.v);

}

} e[maxM];

 

struct edge {

int t;

edge* n;

} EDGE[maxn << 1], *Pt = EDGE, *H[maxn];

 

inline void AddEdge(int u, int v) {

Pt->t = v, Pt->n = H[u], H[u] = Pt++;

}

 

int Find(int x) {

return x == par[x] ? x : par[x] = Find(par[x]);

}

 

void dfs(int x) {

sz[x] = 1, ch[x] = -1;

for(edge* e = H[x]; e; e = e->n) if(e->t != fa[x]) {

fa[e->t] = x;

dep[e->t] = dep[x] + 1;

dfs(e->t);

sz[x] += sz[e->t];

if(!~ch[x] || sz[ch[x]] < sz[e->t]) ch[x] = e->t;

}

}

 

void DFS(int x) {

top[x] = TOP;

Id[x] = ++n;

if(~ch[x]) DFS(ch[x]);

for(edge* e = H[x]; e; e = e->n)

if(e->t != fa[x] && e->t != ch[x]) DFS(TOP = e->t);

}

 

struct Node {

Node *lc, *rc;

int v, t;

inline void upd() {

if(t) {

v = 0;

} else if(lc)

v = lc->v + rc->v;

}

inline void pd() {

if(t && lc) {

lc->t = rc->t = 1;

t = 0;

}

}

} pool[maxn << 1], *pt = pool, *Root;

 

void Build(Node* t, int l, int r) {

t->v = r - l + 1;

t->t = 0;

if(l != r) {

int m = (l + r) >> 1;

Build(t->lc = pt++, l, m);

Build(t->rc = pt++, m + 1, r);

} else

t->lc = t->rc = NULL;

}

 

void Change(Node* t, int l, int r) {

if(!t->v) return;

if(L <= l && r <= R) {

t->t = 1;

} else {

int m = (l + r) >> 1;

if(L <= m) Change(t->lc, l, m);

if(m < R) Change(t->rc, m + 1, r);

}

t->upd();

}

 

int Sum(Node* t, int l, int r) {

if(L <= l && r <= R)

return t->v;

int m = (l + r) >> 1;

t->pd(), t->lc->upd(), t->rc->upd();

return (L <= m ? Sum(t->lc, l, m) : 0) + (m < R ? Sum(t->rc, m + 1, r) : 0);

}

 

void Modify(int u, int v) {

for(; top[u] != top[v]; u = fa[top[u]]) {

if(dep[top[u]] < dep[top[v]]) swap(u, v);

L = Id[top[u]], R = Id[u];

Change(Root, 1, N);

}

if(u == v) return;

if(dep[u] > dep[v]) swap(u, v);

L = Id[u] + 1, R = Id[v];

Change(Root, 1, N);

}

 

int Query(int u, int v) {

int ret = 0;

for(; top[u] != top[v]; u = fa[top[u]]) {

if(dep[top[u]] < dep[top[v]]) swap(u, v);

L = Id[top[u]], R = Id[u];

ret += Sum(Root, 1, N);

}

if(dep[u] > dep[v]) swap(u, v);

L = Id[u] + 1, R = Id[v];

return ret + Sum(Root, 1, N);

}

 

void Work() {

for(int i = 0; i < N; i++) par[i] = i;

for(int i = 0; i < M; i++) if(F[i]) {

int u = Find(e[i].u), v = Find(e[i].v);

if(u != v) {

AddEdge(e[i].u, e[i].v);

AddEdge(e[i].v, e[i].u);

par[u] = v;

} else

F[i] = -1;

}

fa[0] = -1, dep[0] = 0, dfs(0);

DFS(TOP = 0);

Build(Root = pt++, 1, N);

for(int i = 0; i < M; i++)

if(!~F[i]) Modify(e[i].u, e[i].v);

for(int i = qn; i--; ) if(q[i].t) {

ans[i] = Query(q[i].u, q[i].v);

} else

Modify(q[i].u, q[i].v);

for(int i = 0; i < qn; i++)

if(q[i].t) printf("%d\n", ans[i]);

}

 

void Init() {

N = getint(), M = getint();

for(int i = 0; i < M; i++) {

e[i].u = getint() - 1, e[i].v = getint() - 1;

if(e[i].u > e[i].v) swap(e[i].u, e[i].v);

F[i] = 1;

}

sort(e, e + M);

qn = 0;

while((q[qn].t = getint()) != -1) {

q[qn].u = getint() - 1, q[qn].v = getint() - 1;

if(q[qn].u > q[qn].v) swap(q[qn].u, q[qn].v);

if(!q[qn].t) {

F[lower_bound(e, e + M, E(q[qn].u, q[qn].v)) - e] = 0;

}

qn++;

}

}

 

int main() {

Init();

Work();

return 0;

}

----------------------------------------------------------------------------------------

1969: [Ahoi2005]LANE 航线规划

Time Limit: 10 Sec  Memory Limit: 64 MB
Submit: 180  Solved: 87
[Submit][Status][Discuss]

Description

对Samuel星球的探险已经取得了非常巨大的成就，于是科学家们将目光投向了Samuel星球所在的星系——一个巨大的由千百万星球构成的Samuel星系。 星际空间站的Samuel II巨型计算机经过长期探测，已经锁定了Samuel星系中许多星球的空间坐标，并对这些星球从1开始编号1、2、3……。 一些先遣飞船已经出发，在星球之间开辟探险航线。 探险航线是双向的，例如从1号星球到3号星球开辟探险航线，那么从3号星球到1号星球也可以使用这条航线。 例如下图所示：  在5个星球之间，有5条探险航线。 A、B两星球之间，如果某条航线不存在，就无法从A星球抵达B星球，我们则称这条航线为关键航线。 显然上图中，1号与5号星球之间的关键航线有1条：即为4-5航线。 然而，在宇宙中一些未知的磁暴和行星的冲撞，使得已有的某些航线被破坏，随着越来越多的航线被破坏，探险飞船又不能及时回复这些航线，可见两个星球之间的关键航线会越来越多。 假设在上图中，航线4-2（从4号星球到2号星球）被破坏。此时，1号与5号星球之间的关键航线就有3条：1-3，3-4，4-5。 小联的任务是，不断关注航线被破坏的情况，并随时给出两个星球之间的关键航线数目。现在请你帮助完成。

Input

第一行有两个整数N，M。表示有N个星球（1< N < 30000），初始时已经有M条航线（1 < M < 100000）。随后有M行，每行有两个不相同的整数A、B表示在星球A与B之间存在一条航线。接下来每行有三个整数C、A、B。C为1表示询问当前星球A和星球B之间有多少条关键航线；C为0表示在星球A和星球B之间的航线被破坏，当后面再遇到C为1的情况时，表示询问航线被破坏后，关键路径的情况，且航线破坏后不可恢复； C为-1表示输入文件结束，这时该行没有A,B的值。被破坏的航线数目与询问的次数总和不超过40000。

Output

对每个C为1的询问，输出一行一个整数表示关键航线数目。 注意：我们保证无论航线如何被破坏，任意时刻任意两个星球都能够相互到达。在整个数据中，任意两个星球之间最多只可能存在一条直接的航线。

Sample Input

5 5
1 2
1 3
3 4
4 5
4 2
1 1 5
0 4 2
1 5 1
-1

Sample Output

1
3

HINT

Source