01 离散时间信号的时域表示

Posted 2021-12-14 lastknight

离散时间信号的时域表示

??在连续时间系统中，我们表示用\(x(t)\)来表示一个信号，其中\(t\)的取值是连续的，在离散时间系统中，我们\(x[n]\)这个序列来表示一个信号，其中\(n\)的取值只能为整数，对于非整数的n，\(x[n]\)没有定义而不是取值为0。

一个序列可写为
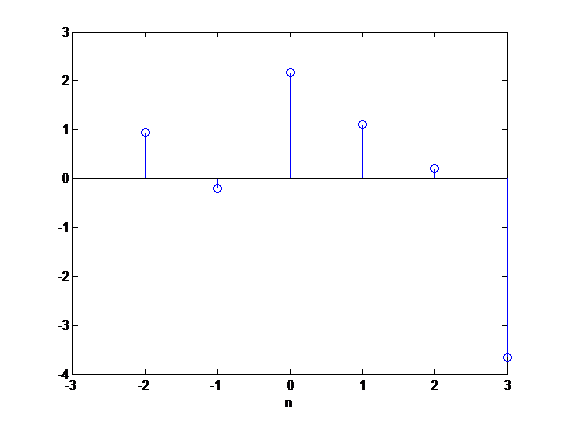
\[ x[n] = \..., 0.95, -0.2,\mathop2.17\limits_\uparrow,1.1,0.2,...\ \]
其中用箭头表示\(x[0]?\)出现的位置。

??离散数字信号从哪里来？离散时间信号的来源主要是两个，第一个直接来源于数据，比如每个月的股市数据就是一个很好的例子，而另一个来源就是对模拟信号进行抽样，然后对抽样过后得到的数字信号进行数字信号处理，然后通过数模转换器转换为模拟信号，从而达到我们的目的。

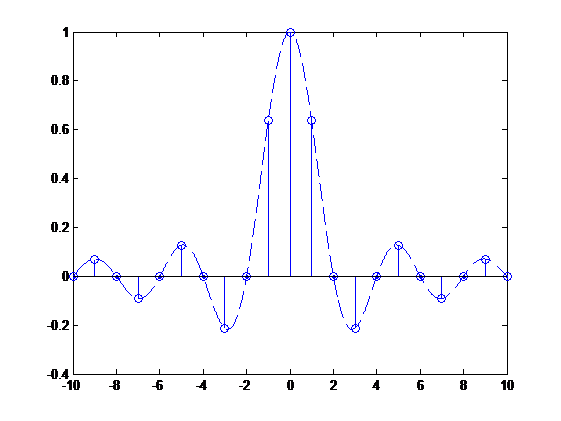
上图便为对连续信号的抽样

离散时间信号的长度

??离散时间可以分为有限长序列和无限长序列，有限长序列就是只在限定的时间段内才有值：
\[ N_1\leq n\leq N_2? \]
那么该有限长序列的长度\(N\)为\(N = N_2-N_1+1\)

无限长序列可分为三类：

右边序列

即，若对于\(x[n] = 0,\quad n<N_1\)，那么称\(x[n]\)为右边序列，特别的，如果\(N_1\geq0\)，那么称\(x[n]\)为因果序列。

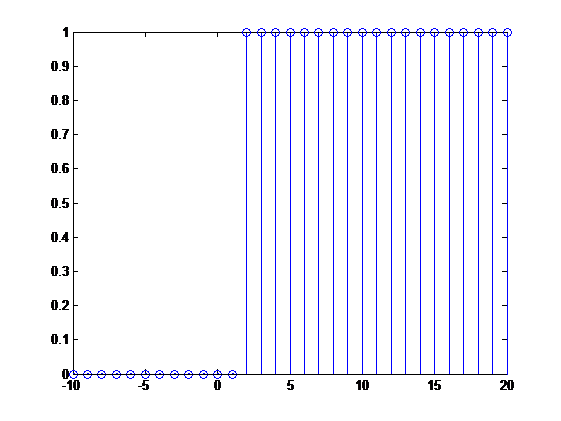
??当\(n< 2=N_1?\)时，\(x[n]=0?\)，所以这是一个右边序列，并且\(N_1\geq0?\)，所以这是一个因果序列。

左边序列

即当\(x[n] = 0,x>N_2\)，那么\(x[n]\)称为左边序列，当\(N_2\leq0\),称\(x[n]\)为反因果序列。

??对于\(n>2=N_2,x[n]=0?\)，所以这是一个左边序列，而\(N_2>0?\)，所以这不是一个反因果序列。

双边序列

一般的双边序列在正的\(n\)和负的\(n\)都有值。

离散时间信号的强度

??离散时间信号的强度由其范数给出，范数的定义如下：
\[ \Vert x\Vert_p=(\sum_n=-\infty^\infty)^1/p \]
其中\(p\)是正整数，最常用的是?\(p=1,2,\infty\)。

??由上面的定义可知，\(L_\infty\)的范数是\(\x[n]\\)的最大值的峰值，即
\[ \Vert x\Vert_\infty = |x|_max \]