伪随机数的产生

Posted 2020-07-27 block2016

应用：随机数或者伪随机数的产生在大量的密码函数中都有广泛的应用。

要求：随机性和不可预测性

　　1、随机性有两个评价标准：分布均匀性和独立性

　　a) 分布均匀性指的是0和1出现的概率大致相等

　　b) 独立性指的是序列中任何子序列不能由其他子序列推导出

　　遗憾的是，没有可靠的方法表明一个序列的独立性好，只能证明一个序列不具有独立性。因此只好多测测，来回多次仍然表现不错的话，就姑且当它独立性不错啦。

　　2、不可预测性是指每个数都统计独立于其他数，因而不可预测。但是真正的随机数序列很少用，一般看上去随机的随机数序列都是由算法产生的。因此需要注意不能让攻击者从先前的随机数推导出后面的随机数。

 

TRNG、PRNG和PRT

　　

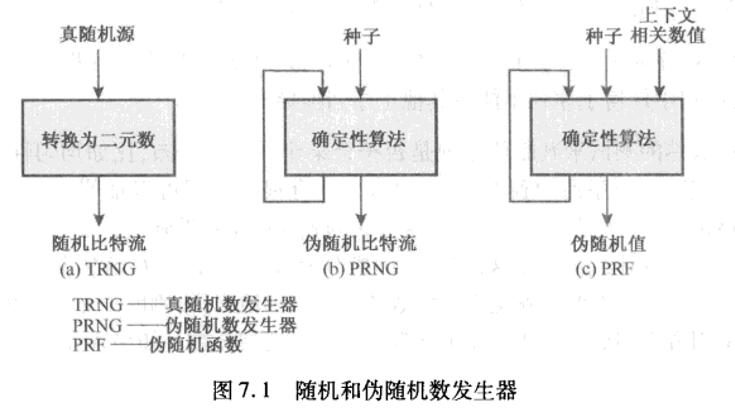
　　真随机数发生器TRNG的关键在于其输入源非常随机，一般是从物理环境中抽取，如键盘敲击时间模式、磁盘的电活动、鼠标移动、系统时间的瞬时值等，这个源通常叫做熵源。

　　伪随机数发生器PRNG则使用种子作为输入。攻击者知道算法和种子就可以重现输出流。

　　伪随机数函数PRF与PRNG的区别在于产生的位数量不同，PRNG产生不限长的位流，而PRT则产生固定长度的伪随机位串。此外PRT通常除了种子，还会加上一些上下文作为输入。PRNG和PRT两者没有本质的差异，可以使用相同的算法。

　　PRNG可产生用于流密码的伪随机位流，而PRT则可用于产生对称密码的密钥。

 

对PRNG和PRT保密性的要求

　　1、随机性

　　a) 均匀性

　　b) 可伸缩性：任何子序列都应该通过随机性测试

　　c) 一致性：对所有的种子，产生的序列及其子序列都应该通过随机性测试。

　　2、不可预测性

　　a) 前向不可预测性：不知道种子情况下，不管知道序列多少位，都无法预测下一位。

　　b) 后向不可预测性：从产生的任何值都不能推断出种子值。即种子和该种子产生的任意值之间没有相关性

　　3、种子的要求

　　为了达到种子不可预测的目的，通常使用TRNG来产生种子。

　　不直接用TRNG的原因

　　　　1、TRNG无法产生任意长度的随机数位流

　　　　2、TRNG可能会产生不平衡的二元序列，随机化效果不好，因此即使是有限数量的位，也是用TRNG产生种子给PRT来产生伪随机位串。

 

伪随机数发生器算法设计

　　PRNG算法大体分两类

　　1、特意构造的算法

　　　　这些算法是为了产生伪随机位流而专门设计的，最重要的例子是RC4

　　2、基于现存密码算法的算法

　　　　密码学算法在PRNG中起核心作用，三大类密码学算法常用来产生PRNG

　　　　对称分组密码、非对称密码、Hash函数和消息认证码

 

线性同余发生器和BBS发生器

　　1、线性同余发生器

　　　　随机数序列产生公式

　　　　　　X_n+1 = (aX_n + c) mod m      m,a,c,X₀∈Z 

　　　　参数取值需要满足三个标准：函数在重复前应该产生0-m之间的所有数；产生的序列应该显得随机；生成函数可以用计算机方便地实现

 

　　　　满足条件的参数选择如下：

　　　　m一般取素数，且要求很大，对于32位机一般取值为2³¹-1

　　　　a 的可取值不多，当a=7⁵=16807时满足以上标准。

 

　　　　这个算法的缺点是，在参数确定后，伪随机序列只与X₀相关，容易被破解。有一种改进的办法就是每隔N个数就以时钟值对m取模作为新的种子来产生新的序列。还有一种方法是直接将随机数加上时钟值再对m取模。

 

　　2、BBS发生器(三位设计者名字首字母合称)

　　　　产生过程如下：

　　　　首先，选择两个大素数p和q，且要求 p ≡ q ≡ 3 (mod 4)，令n = p × q

　　　　接着选择一个随机数s，要求s与n互素，然后按以下算法产生位B_i序列

　　　　　　X₀ = s² mod n

　　　　　　for i = 0 to ∞

　　　　　　　　X_i = (X_i-1)² mod n

　　　　　　　　B_i = X_i mod 2         //每隔循环都取最低有效位

 

　　　　BBS发生器是产生安全伪随机数的普遍算法，是特意构造算法中密码强度有最强公开证明的一个，被称为密码安全伪随机位发生器(CSPRBG)。

　　　　BBS之所以被称为安全伪随机位生成器，是因为它能经受续位测试。续位测试是指给定序列的最开始k位，没有任何有效算法可以产生超过1/2的概率预测出第(K+1)位。因此对于实际应用，这个序列是不可预测的。

　　　　BBS的安全性是基于对n的因子分解的困难性上的。

 

使用分组密码的伪随机数的产生

　　　　有两种分组密码的工作模式在构建PRNG上获得了广泛的接受：CTR模式和OFB模式。

 

ANSI X9.17伪随机数发生器

　　　　该伪随机数发生器是密码学意义上最强的伪随机数发生器之一，应用在金融安全和PGP上。

　　　　它使用了3DES来加密，下图说明了算法流程

　　　　

　　　　

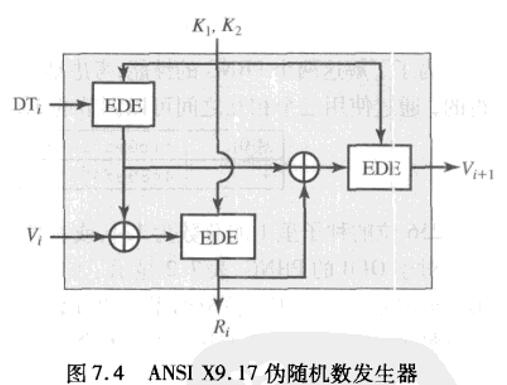
　　　　DT_i：算法第i轮开始时的日期/时间值，64位，每一轮都被更新。

　　　　V_i：算法第i轮开始时的种子值，64位，每一轮都被更新。

　　　　R_i： 算法第i轮所产生的伪随机数。

　　　　K₁，K₂：各阶段算法所用的DES密钥，各56位。

　　　　可用以下表达式描述该算法：

　　　　　　R_i = EDE([K_1,K₂],[V_i⊕EDE([K_1,K₂],DT_i)])

　　　　　　V_i+1 = EDE([K_1,K₂],[R_i⊕EDE([K_1,K₂],DT_i)])

　　　　该方法的密码强度来自几个方面，包括112位密钥和3个EDE共计9次DES加密。