计算机程序可以产生真正的随机数吗？不是random伪随机

Posted 2023-04-29

光靠程序是无法实现真随机数的。要实现真正的随机数，必须有真正随机的种子。

在计算机中并没有一个真正的随机数发生器，但是可以做到使产生的数字重复率很低，这样看起来好象是真正的随机数，实现这一功能的程序叫伪随机数发生器。

有关如何产生随机数的理论有许多，如果要详细地讨论，需要厚厚的一本书的篇幅。不管用什么方法实现随机数发生器，都必须给它提供一个名为“种子”的初始值。而且这个值最好是随机的，或者至少这个值是伪随机的。“种子”的值通常是用快速计数寄存器或移位寄存器来生成的。

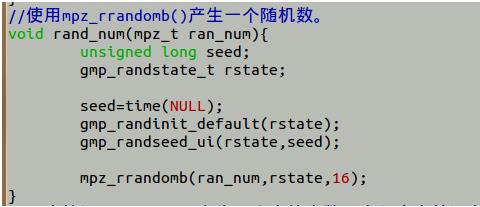
扩展资料：

随机数在密码学中非常重要，保密通信中大量运用的会话密钥的生成即需要真随机数的参与。如果一个随机数生成算法是有缺陷的，那么会话密钥可以直接被推算出来。若果真发生这种事故，那么任何加密算法都失去了意义。

密码学中大量利用伪随机数生成器的应用还有流密码。流密码的著名例子是RC4。流密码的原理是利用一个密码学安全的伪随机数生成器根据密钥产生一串密码学安全的伪随机比特列，再将消息与上述随机比特列按位异或运算。

参考资料来源：百度百科-随机数

参考技术A 光靠程序是无法实现真随机数的。要实现真正的随机数，必须有真正随机的种子。追问

不是说量子力学中粒子的位置是随机的吗？量子计算机可以用来实现真正的随机吗？还有不可以在程序外关联一个能制造随机的硬件装置呀，比如一个超高速的掷硬币装置，我试了用蒙特卡洛这种利用概率的算法求圆周率不是很精确，我想就是因为random这毕竟是伪随机，如果是真正的随机的话，无论是理论上还是显示我感觉应该很精确，至少比祖冲之求的精确

本回答被提问者和网友采纳 参考技术B 可以追答

我们上次正确的的数和用计算机的数差好多

追问

是怎么个算法呢，

追答

那只是偶然情况

用笔算

追问

伪随机数后面都是有一个算法的，算法意味着是要有逻辑的，既函数，无论表面看起来多么随机，其实背后不还是有一个规律吗

追答

如果用计算机算多算几遍

听不懂

追问

但是不是说量子屋里月中量子的下一刻的位置是真正的不可测的，随机的，可以把他结合到程序中吗

或者程序的背后绑定一个实物装置，比如高速的掷硬币

追答

我要晕了

我懂的不多自是个小学女生

追问

量子计算机是干什么的呀

追答

嗯嗯嗯嗯额

我查查

执行指令的

后面的我忘了

追问

你上小学吗，那你知道圆周率么

追答

知道

追问

你知道圆周率怎么求吗

追答

3.1415926535……

我刚刚上厕所

人那

你也去上厕所

兀

追问

可以用随机数计算这个派，但是这个随机数其实是伪随机数，所以说还是有些误差的，要是没有真正的随机数就好了，就像掷硬币那样的，下一刻是绝对纯概率的，所以最近在纠结这个问题

追答

额

追问

蒙特卡洛求算法求圆周率

追答

啥

抛硬币也有立着的时候

追问

我希望有一些志同道合的朋友讨论讨论，原来你真是个00后哇

你可以买彩票了

追答

什么是OO后

为什么可以买了

追问

指十几岁的孩子

追答

噢

我12

追问

硬币立着的几率和中彩票差不多

追答

我立着过好次

追问

我12时还没见过大哥大呢

追答

大哥大是啥

追问

你那是桶还是硬币呀

追答

你多少岁

硬币

追问

我是最大的九零后，你算算

追答

20多岁是吗

追问

对

追答

我是算命先生

追问

你们现在小学生都有手机吗

追答

有

追问

几个

追答

只不过这不是我的我的在充电

2个

追问

你们好幸福呀，根本不用担心作业了

追答

……

为啥

追问

我们那时天天买资料书抄答案

追答

我很利害的

追问

不错

追答

我以经破过好多道全班都没做出的题

追问

是数学题吗，我数学最差了，真厉害

你们教室提供免费wifi么？

追答

是数学

提拱

我刚才写作业1了

我还没写完

追问

你们数学老师厉害吗

追答

你好

人

这几天我爸出门了

所以没玩

对不起

不利害

你好

参考技术C 光靠程序是无法实现真随机数的。要实现真正的随机数，必须有真正随机的种子。

Insecure Randomness 不安全的随机数

Insecure Randomness

Abstract

标准的伪随机数生成器不能抵挡各种加密攻击。

Explanation

在对安全性要求较高的环境中，使用一个能产生可预测数值的函数作为随机数据源，会产生 Insecure

Randomness 错误。 电脑是一种具有确定性的机器，因此不可能产生真正的随机性。 伪随机数生成器

(PRNG) 近似于随机算法，始于一个能计算后续数值的种子。 PRNG 包括两种类型： 统计学的 PRNG 和密

码学的 PRNG。 统计学的 PRNG 可提供有用的统计资料，但其输出结果很容易预测，因此数据流容易复制。

若安全性取决于生成数值的不可预测性，则此类型不适用。 密码学的 PRNG 通过可产生较难预测的输出结果

来应对这一问题。 为了使加密数值更为安全，必须使攻击者根本无法、或极不可能将它与真实的随机数加以

区分。 通常情况下，如果并未声明 PRNG 算法带有加密保护，那么它有可能就是一个统计学的 PRNG，不应

在对安全性要求较高的环境中使用。

示例： 下面的代码可利用统计学的 PRNG 为购买产品后仍在有效期内

的收据创建一个 URL。

String GenerateReceiptURL(String baseUrl) {
    Random ranGen = new Random();
    ranGen.setSeed((new Date()).getTime());
    return(baseUrl + Gen.nextInt(400000000) + ".html");
}

 

这段代码使用 Random.Next() 函数为由其产生的收据页面生成“唯一”的标识符。 因为

Random.nextInt() 是一个统计学 PRNG，攻击者很容易就能猜到由它生成的字符串。 尽管收据系统的底

层设计也存在错误，但如果使用了一个不生成可预测收据标识符的随机数生成器（如密码学的 PRNG），会

更安全一些。

Recommendation

当不可预测性至关重要时，如大多数对安全性要求较高的环境都采用随机性，这时可以使用密码学的 PRNG

。 不管选择了哪一种 PRNG，都要始终使用带有充足熵的数值作为该算法的种子。 （诸如当前时间之类的数

值只提供很小的熵，因此不应该使用。） Java 语言在 java.security.SecureRandom 中提供了一个加

密 PRNG。 就像 java.security 中其他以算法为基础的类那样，SecureRandom 提供了与某个特定算法

集合相关的包，该包可以独立实现。 当使用 SecureRandom.getInstance() 请求一个 SecureRandom

实例时，您可以申请实现某个特定的算法。 如果算法可行，那么您可以将它作为 SecureRandom 的对象使

用。 如果算法不可行，或者您没有为算法明确特定的实现方法，那么会由系统为您选择 SecureRandom 的

实现方法。 Sun 在名为 SHA1PRNG 的 Java 版本中提供了一种单独实现 SecureRandom 的方式，Sun 将其

描述为计算： “SHA-1 可以计算一个真实的随机种子参数的散列值，同时，该种子参数带有一个 64 比特的计

算器，会在每一次操作后加 1。 在 160 比特的 SHA-1 输出中，只能使用 64 比特的输出 [1]。” 然而，文档中

有关 Sun 的 SHA1PRNG 算法实现细节的相关记录很少，人们无法了解算法实现中使用的熵的来源，因此也并

不清楚输出中到底存在多少真实的随机数值。 尽管有关 Sun 的实现方法网络上有各种各样的猜测，但是有一

点无庸置疑，即算法具有很强的加密性，可以在对安全性极为敏感的各种内容中安全地使用。

解决办法：

采用更加安全的SecureRandom来替换Random。