ST表！

Posted 2021-11-26 gengyf

Pre-Scene

我们有一道小水题

给出一个长度为n的序列，m次询问，每次询问区间内的最大值

有大佬说，线段树秒切

另一个大佬说，用什么线段树，我树状数组比你还码量少，一样秒切

ST表...神秘的大佬在角落里出声…

什么！大佬们回头喊道

                                                                                                                                                                                                         

关于ST表

确实，关于求区间最值，线段树和树状数组已经很nice了，但是，对于静态区间最值，我们还有更优秀的——ST表

其预处理复杂度为O(log n),而查询是O(1)的！

对于离线的题目，用码量少不易出错（我写线段树从没一遍过过）且较快的ST表，是更优的

原理  以一种类似于二分的思想，把要查询的区间分成两个小区间分别查询最值，由小区间找到大区间的最小值

算法实现

最值是通过一个 st[i][j] 数组来储存的

st[i][j] 是存的从 i 开始的 2^j 个数中的最大值，即区间[ i , i+2^j ) 的最值

预处理

void chuli(){

　　for(int j=1;j<=21;j++)         //j<=21是因为题目数据在1e6内
   　　for(int i=1;i+(1<<j)-1<=n;i++){     //区间[i,i+2^j)
      　　st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);  //区间[i,i+2^j)的最值由[i,i+2^(j-1))和[i+2^(j-1),i+2^j)转移过来  
    }
}

来画个图理解下

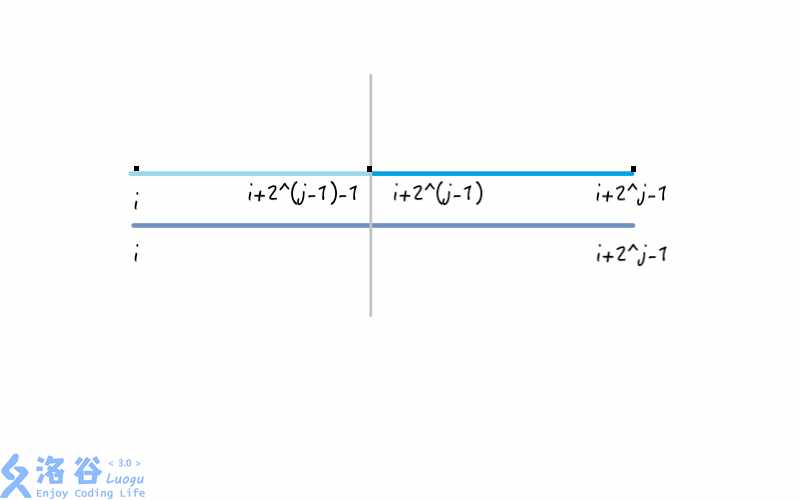
根据初中数学知识，易得 i+2^(j-1) 是这段区间的中点（这里呼应了上文的二分思想）

这样我们就把一段较长的区间分成了两个小区间，再取两个小区间最值的最值，即可得到大区间的最值

查询

int qurey(int l,int r){
    int k=log2(r-l+1);       //求出 log2(区间长度)，这样可以保证一定可以覆盖要查询的区间
    return max(st[l][k],st[r-(1<<k)+1][k]);  //此处将 k 带入即可轻松理解
}

 

为什么能保证一定可以覆盖呢？再来张图

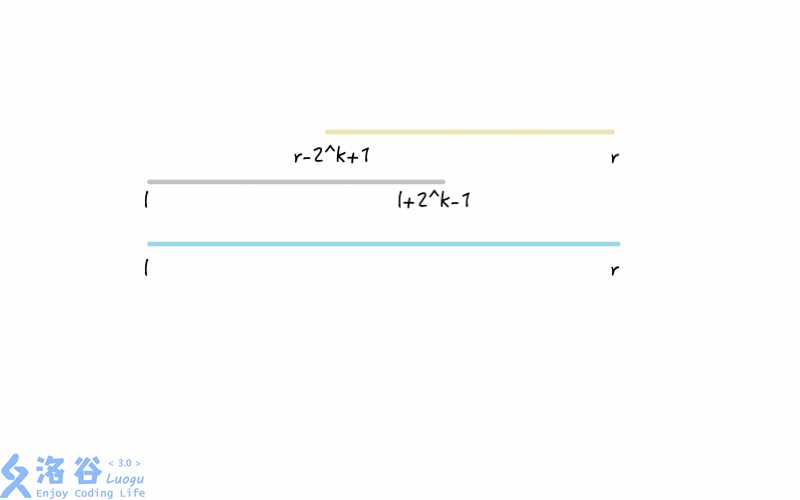
对于左右端点分别查询，就保证了区间被完全覆盖

 

洛谷板子P3865 传送门

#include<cstdio>
#include<algorithm>
#include<cmath>
using namespace std;
int st[100005][21];
int n,m;
int qurey(int l,int r){
    int k=log2(r-l+1);
    return max(st[l][k],st[r-(1<<k)+1][k]);
}
void chuli(){
　　for(int j=1;j<=21;j++)
　　    for(int i=1;i+(1<<j)-1<=n;i++){
　　　　　　st[i][j]=max(st[i][j-1],st[i+(1<<(j-1))][j-1]);
　　　　}
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++){
        scanf("%d",&st[i][0]);   //想一想，为什么这么输入
    }
　　 chuli();
    for(int i=1;i<=m;i++){
        int l,r;
        scanf("%d%d",&l,&r);
        printf("%d\\n",qurey(l,r));
    }
    return 0;
}

 后记：自从小蒟蒻发现了ST表这种好用的东西，静态区间最值再没写过线段树 (*^__^*) 

          pre-scene里的小水(S)题(T)，其实已经说明了这题的做法 O(∩_∩)O~