a(n+1) = f[a(n)] 型递推数列的迭代作图（玩计算器玩出了问题）

Posted 2020-07-26 假如你是李华

把任意一个正数开平方再加 \\(1\\), 把得到的结果也开平方再加 \\(1\\), 不断算下去，最终总会得到 \\( \\frac{3+\\sqrt{5}}{2} \\approx 2.61804 \\), 即：

\\( \\sqrt{\\cdots \\sqrt{\\sqrt{\\sqrt{x}+1}+1}+1}+1 = \\frac{3+\\sqrt{5}}{2} \\;\\;\\;\\; (x>0) \\)

这是某同学玩计算器时发现的，非常有意思。不管一开始给的数是多少，终最都会停在这个神奇的数上，它是黄金比 \\( \\frac{\\sqrt{5}+1}{2} \\) 的平方。

比如代入 \\(x=2\\), 成立：

代入 \\(x=20\\), 也成立：

把算式从 \\( \\sqrt{x}+1 \\) 换成 \\( \\sqrt{x}+2 \\) 也有类似结论：

---

也就是说，递推数列

\\( a_{n+1} = \\sqrt{a_{n}}+1 \\;\\;\\;\\; (a_{1}>0) \\)

在 \\( n \\rightarrow +\\infty \\) 时，收敛于 \\( \\frac{3+\\sqrt{5}}{2} \\). 把 \\(+1\\) 换成加别的正数也有类似结论，只是收敛到的值不同。

那么，问题来了：这是为什么呢？为什么收敛？为什么极限是这个数，而且与 \\( a_{1} \\) 无关？

我在网上提问后，得到了这样的答案：

你看，如果这个数列在 \\( n \\rightarrow +\\infty \\) 时收敛的话，那么当 \\(n\\)「很大很大」的时候，\\( a_{n+1} 和 a_{n} \\) 就是一个东西了，即：

\\( \\lim_{n \\rightarrow +\\infty} a_{n} = \\lim_{n \\rightarrow +\\infty} a_{n+1} \\)

将递推式代入可得：

\\( \\lim_{n \\rightarrow +\\infty} a_{n} = \\lim_{n \\rightarrow +\\infty} (\\sqrt{a_{n}}+1) \\)

\\( \\lim_{n \\rightarrow +\\infty} a_{n} = \\left (\\lim_{n \\rightarrow +\\infty} \\sqrt{a_{n}} \\right )+1 \\)

\\( \\lim_{n \\rightarrow +\\infty} a_{n} = \\sqrt{ \\lim_{n \\rightarrow +\\infty} a_{n} }+1 \\)

令 \\( x = \\lim_{n \\rightarrow +\\infty} a_{n} \\), 得：

\\( x = \\sqrt{x}+1 \\)

解得

\\( x = \\frac{3+\\sqrt{5}}{2} \\)

这一答案有理有据，解释了为什么极限与 \\( a_{1} \\) 无关，并且解出了这个极限。可「为什么收敛」的问题，还是没有解决。

---

 后来不知从哪里看到一个作图方法，正好可以解决这个问题。虽然不是严格证明，但非常直观。

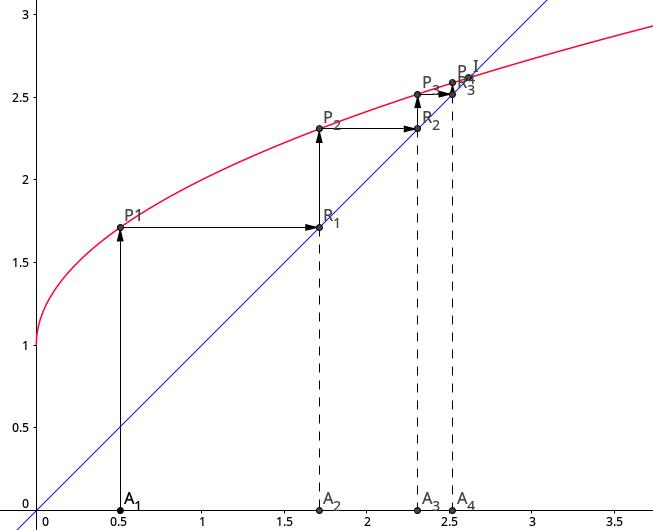
如图，蓝色直线（设为 \\(l\\)）是 \\( y = x \\), 红色曲线（设为 \\(m\\)）是 \\( y = \\sqrt{x}+1 \\), 它们的交点 \\(I\\) 的横坐标 \\(I_{x}\\) 即是方程 \\( x = \\sqrt{x}+1 \\) 的解，也就是数列的极限。

在 \\(x\\) 轴上取点 \\(A_{1}(a_{1},\\; 0)\\), 过 \\(A_{1}\\) 作竖直直线交 \\(m\\) 于 \\(P_{1}\\). 此时 \\(P_{1}\\) 的纵坐标为 \\(\\sqrt{a_{1}}+1\\), 即 \\(a_{2}\\). 这相当于完成了第一次代入。

为了进行第二次代入，以求出 \\(a_{3}\\), 我们可以过 \\(P_{1}\\) 作水平直线交 \\(l\\) 于 \\(R_{1}\\), \\(R_{1}\\) 在 \\(x\\) 轴上的投影设为 \\(A_{2}\\), 它的横坐标是 \\(A_{2}\\).

这时。我们就可以像刚才的 \\(A_{1}\\) 一样，过 \\(A_{2}\\) 作竖直直线交 \\(m\\) 于 \\(P_{2}\\), 求出 \\(a_{3}\\) …… 一直重复这个过程，就会在 \\(x\\) 轴上留下一串点 \\( A_{1}\\;A_{2}\\;A_{3}\\cdots \\), 它们的横坐标就是数列的各项 \\( a_{1}\\;a_{2}\\;a_{3}\\cdots \\) .

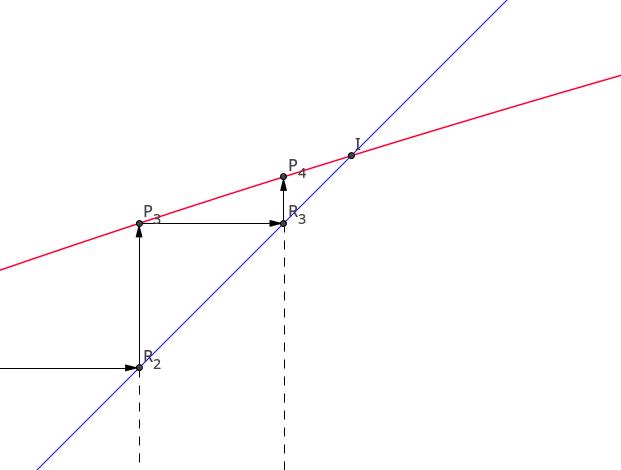
两条曲线中间留下了一个阶梯状的图形。很容易看出，这个「阶梯」是穿不过 \\(I\\) 点的，而且随着 \\(n\\) 趋于无穷大，\\(P_{n}\\) 点无限趋近于 \\(I\\) 点。这就说明了数列 \\(\\{a_{n}\\}\\) 收敛于 \\(I_{x} = \\frac{3+\\sqrt{5}}{2}\\) .

这个作图方法适用于各种 \\( a_{n+1} = f(a_{n}) \\) 形的递推数列，比如下面这个 \\(a_{n+1} = \\cos(a_{n})\\) :

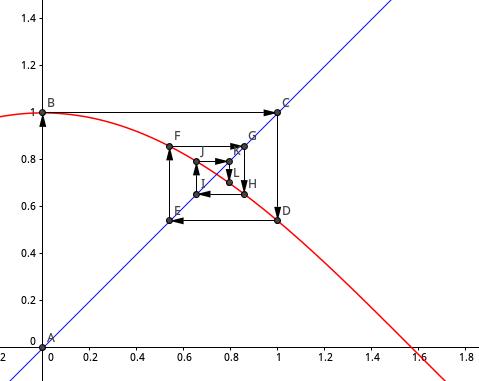
只不过这个就不是阶梯形的了，而是螺旋形的，一圈一圈地往里转。

 至此，终于打破沙锅问到底，把玩计算器玩出的问题解决了。