概率论复习

Posted 2020-06-13

一、随机变量的数字特征

1. 数学期望

• 刻画随机变量取值的平均数，若X,Y相互独立，则E(XY)=E(X)E(Y)

 

2. 方差

• 刻画随机变量取值的离散程度
• 定义
  方差：D(x) = E{[X-E(X)]^2}
  标准差：sigma(x) = sqrt(D(x))
• 常用计算公式
  D(X)=E(X^2)-[E(X)]^2
• 性质
  1. D(CX) = C^2 * D(X)
  2. D(X)+D(Y)=D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
     D(X)-D(Y)=D(X)+D(Y)-2E{[X-E(X)][Y-E(Y)]}
     if X,Y相互独立,则：=D(X)+D(Y)

分布	期望E	方差D
二项分布B(n,p)	np	np(1-p)
泊松分布P(lambda)	lambda	lambda
均匀分布U(a,b)	(a+b)/2	(b-a)^2/12
指数分布exp(lambda)	1/lambda	1/(lambda^2)
正态分布N(mu,sigma)	mu	sigma^2

3. 协方差

• 随机变量X与Y的协方差：
  cov(X,Y) = E{[X-E(X)][Y-E(Y)]}
  D(X):=cov(X,X)
• 性质：
  1.对称性:cov(X,Y)=cov(Y,X)
  2.齐性：cov(aX,bY)=ab*cov(X,Y)
  3.可加性：cov(X1+X2,Y)=cov(X1,Y)+cov(X2,Y)
• 常用计算公式：
  cov(X,Y)=E(XY)-E(X)E(Y)
• 协方差矩阵：n维随机变量(X1,X2,...,Xn)

 

4. 相关系数

• rho(X,Y)=cov(X,Y)/sqrt[D(X)*D(Y)]，是量纲为1的量
• 性质：
  1.rho(X,Y)可理解为X,Y标准化后的协方差
  2.|rho(X,Y)|<=1
  3.|rho(X,Y)|=1 <==> P{Y=aX+b}=1完全线性相关

 

5. 矩

• 随机变量更一般的数字特征：矩
• 定义：
  X的k阶原点矩：gamma(k)=E(X^k), k=1,2,3,...
  k阶绝对原点矩：alpha(k)=E(|X|^k), k=1,2,3,...
  X的k阶中心矩：mu(k)=E{[X-E(X)]^k}, k=1,2,3,...
  X的k阶绝对中心矩：beta(k)=E{|X-E(X)|^k}, k=1,2,3,...
• 常见：
  gamma(1)=E(X)
  mu(1)=0
  mu(2)=D(X)=gamma(2)-gamma(1)^2

 

二、大数定律和中心极限定理

1. 切比雪夫Chebyshev不等式

• 是对概率作的一个粗略的估计
• P{|X-E(X)|>=eps} <= D(X)/(eps^2)，eps>0
• 例子：当eps=sigma时，
  P{|X-E(X)|>=3sigma} <= sigma^2/(3sigma)^2 = 1/9

 

2. 大数定律

• 如X1,X2,...,Xn的期望均存在,对于任意eps>0，有：
  
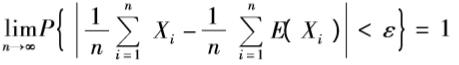
  则称：随机变量序列X1,X2,...,Xn服从大数定律
• 理解：
  1.随机变量序列依概率收敛

 

3. 中心极限定理

• 相互独立的随机变量序列X1,X2,...,Xn的E与D均存在
  X_sum = sum(Xi)=X1+X2+...+Xn的期望与方差：
  E(X_sum) = sum[E(Xi)]
  D(X_sum) = sum[D(Xi)]
• 将X_sum标准化后：
  Zn=X_sum-E(X_sum)/sqrt[D(X_sum)]
  E(Zn)=0
  D(Zn)=1
• 记Zn的分布函数为Fn(x):=P(Zn<=x}，若:
  
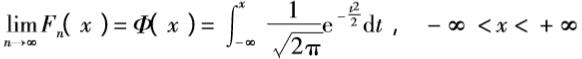
  则称：随机变量序列X1,X2,...,Xn服从中心极限定理
• 理解
  1.{Zn}依分布收敛于标准正态分布随机变量
  2.现实中许多随机变量Z都可以表示为大量的相互独立的随机变量之和，而且其中每一个随机变量对综合的影响十分微小，这类随机变量Z往往近似服从正态分布

 

四、应用 

    蒙特卡罗方法