直线圆其他图形可以将一个无限大的平面分成的块数

Posted 2021-02-14 BobHuang

 3Blue1Brown有个视频，就是在一个马克杯上画三个不同的房子，还有三哥不同的设施(供气、供电和供水)，每一个房子都要连接三个设施

一共要画九条线，任意两条线不能相交  【官方双语】众多科普YouTuber深陷图论谜题，谜底竟然...

这个问题是不可解的，很多大神也画不出来，因为Euler公式23333(欧拉简直太神了)

Euler公式是说，在一个由若干顶点和它们之间的一些不相交的边所组成的图中，等式V+F=E+2总成立

其中V表示顶点个数，E表示总的边数，F表示这个图分割出来的区域个数（包括一个“外部区域”，例如一个圆把平面分割为两个区域）。

现在我们证明下标题的问题，考虑用一个无限大的圆去包裹当前的图形，但是会额外长生一个外区域，需要减去

比如一条直线，可以产生2个交点3条边，就是3-2+1=2

两条直线，平行 产生4个交点6条边，就是6-4+1=3

                 相交于1点 产生5个交点8条边就是8-5+1=4

三条直线  平行 产生6个交点9条边 就是9-6+1=4

                 相交于1点 产生7个交点12条边就是12-7+1=6

                 相交于2点 产生8个交点13条边就是13-8+1=6 //前一个状态多个平行，多两个区域

                 相交于3点 产生9个交点15条边就是15-9+1=7

当然是交点最多点最多了，交点个数=直线条数*(直线条数-1)/2，这些交点会产生[2*交点个数-直线条数]条边，外面补圆了呢，每条直线都要多4条边，多两个顶点

所以这个用n表示直线条数所得关系式为F=4n+2*n(n-1)/2-n-n(n-1)/2-2*n+1=n*(n-1)/2+n+1=n*(n+1)/2+1(n>1)

n=1也成立，所以满足通项公式

如果确定m个点呢，这些点产生的边可能是不同的

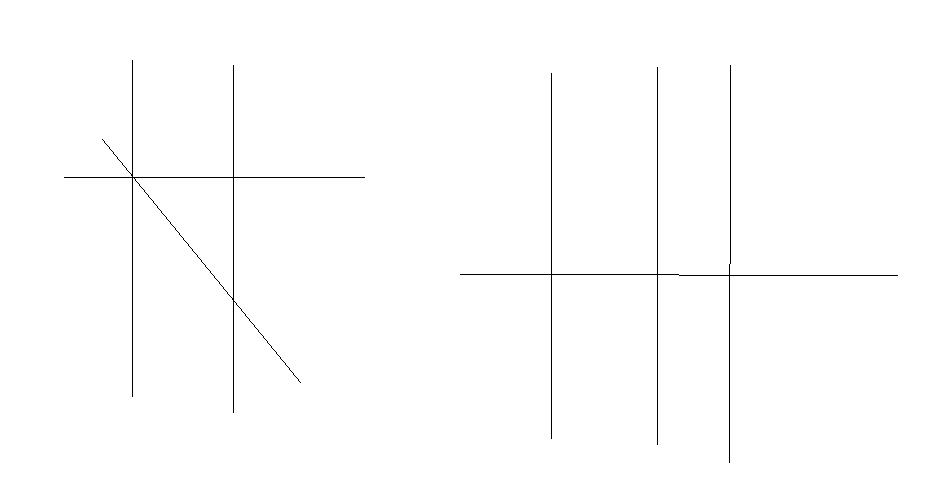
所以是交点问题，下面将会解决(其实和几条直线共用的交点个数有关)

圆的话，相当于少画一个圆，然后区域数不需要-1，即m*(m-1)+2

然后可以去做做TZOJ 4689和3974 题解:TOJ 3974: Region n条直线m个圆最多将圆分为几个区域  TOJ 4689: Sawtooth

然后我们来解决 

3681: 平面分割 

Time Limit(Common/Java):5000MS/15000MS     Memory Limit:65536KByte
Total Submit: 8            Accepted:2

Description

 

给定一系列直线，能够将一个无限大的平面分割成多少块？

 

Input

 

输入数据的第一行为整数N（N<=3000）,接下来有N行，每行有4个整数x1 y1 x2 y2，其中(x1,y1)和（x2,y2）表示平面内的一条直线（即两端点不重合），坐标值的绝对值不大于10000. 任意两条直线不重合。

 

Output

 

输出为一个整数，即这些直线能够将平面分割成的块数。

 

Sample Input

4
5 0 0 5
4 0 4 5
2 4 3 4
1 1 1 5

Sample Output

 9

让我们求一般情况下的解，从以上看好像是n+m+1，但是这个m是没有重合的

其实就是点数对应一个值，因为x条直线交于一点会产生x*(x-1)/2个，但是根据切割你可以发现会产生x-1个区域，可以想下切蛋糕

这题还有个问题就是浮点数判断相等，不能直接判断，因为有有效位数，可以fabs进行eps的比较

点太多了只能分开求

#include<bits/stdc++.h>
using namespace std;
const double eps=1e-10;
struct TT
{
    double x,y;
    bool operator<(const TT &p) const
    {
        return x<p.x||x==p.x&&y<p.y;
    }
    bool operator==(const TT &p) const
    {
        return fabs(x-p.x)<=eps&&fabs(y-p.y)<=eps;
    }
} a[3005];
int X1,X2,Y1,Y2,tot;
struct T
{
    int a,b,c;
    void read()
    {
        scanf("%d%d%d%d",&X1,&Y1,&X2,&Y2);
        a=Y1-Y2,b=X2-X1,c=X1*Y2-X2*Y1;
    }
} p[3005];
inline void la(T A,T B)
{
    double res=A.a*B.b-B.a*A.b;
    if(fabs(res)>eps)a[tot++]={(A.b*1.*B.c-B.b*1.*A.c)/res,(B.a*1.*A.c-A.a*1.*B.c)/res};
}
int main()
{
    int n;
    scanf("%d",&n);
    int ans=n+1;
    for(int i=0; i<n; i++)
    {
        tot=0,p[i].read();
        for(int j=0; j<i; j++)la(p[i],p[j]);
        sort(a,a+tot),ans+=tot;
        for(int i=1; i<tot; i++)if(a[i]==a[i-1])ans--;
    }
    printf("%d",ans);
    return 0;
}

以下是可以验证结论的MLE代码，其实两个差不多的。因为都是求交点，要算一下交点重复多次的影响，就是1+...+n的等差数列

#include<bits/stdc++.h>
using namespace std;
const int N=4.5e6;
const double eps=1e-10;
struct TT
{
    double x,y;
    bool operator<(const TT &p) const
    {
        return x<p.x||x==p.x&&y<p.y;
    }
    bool operator==(const TT &p) const
    {
        return fabs(x-p.x)<=eps&&fabs(y-p.y)<=eps;
    }
}a[N];
int X1,X2,Y1,Y2,tot;
struct T
{
    int a,b,c;
    void read()
    {
        scanf("%d%d%d%d",&X1,&Y1,&X2,&Y2);
        a=Y1-Y2,b=X2-X1,c=X1*Y2-X2*Y1;
    }
} p[3005];
inline void la(T A,T B)
{
    double res=A.a*B.b-B.a*A.b;
    if(fabs(res)>eps)a[tot++]={(A.b*1.*B.c-B.b*1.*A.c)/res,(B.a*1.*A.c-A.a*1.*B.c)/res};
}
int main()
{
    unordered_map<int,int>SS;
    int n;
    scanf("%d",&n);
    for(int i=2; i<=n; i++)SS[i*(i-1)/2]=i-1;
    for(int i=0; i<n; i++)
    {
        p[i].read();
        for(int j=0; j<i; j++)la(p[i],p[j]);
    }
    sort(a,a+tot);
    int ans=n+1,t=1;
    for(int i=1;i<tot;i++)
        if(a[i]==a[i-1])t++;
        else ans+=SS[t],t=1;
    printf("%d",ans+SS[t]);
    return 0;
}