抛物线的几何性质(传统几何法推导)
Posted 假如你是李华
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了抛物线的几何性质(传统几何法推导)相关的知识,希望对你有一定的参考价值。
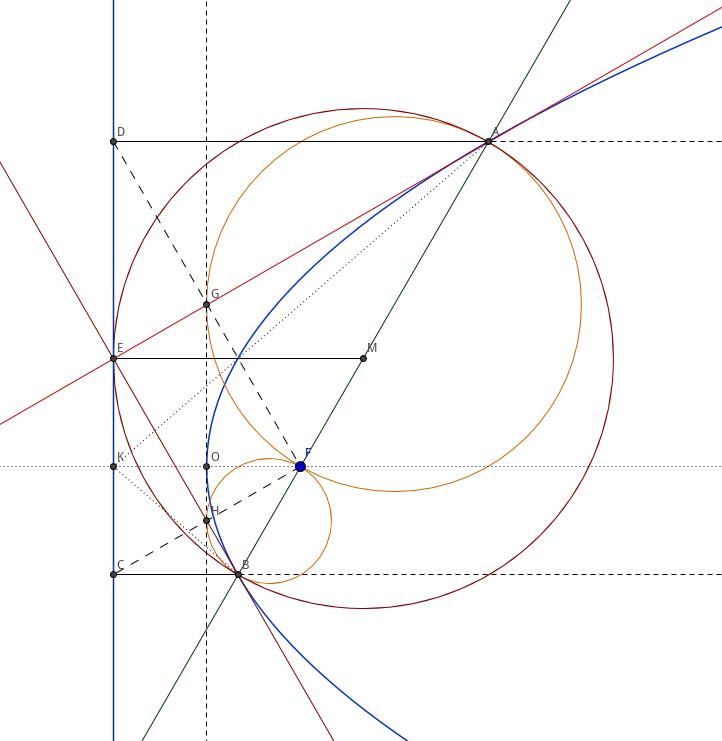
抛物线有很多几何性质,网上也有不少关于这些性质的推导的文章,不过几乎清一色地都是用的解析几何的方法。联立方程,导出根与系数的关系,算算算算算……
但是,与同样是二次曲线的椭圆和双曲线不同,圆和抛物线的几何性质非常「好」,不用坐标法,也能推出很多结论。不过相比具有完美对称性的圆来说,抛物线还是逊色了许多。圆的切线很容易用几何条件去描述(容易用反证法证出圆的切线垂直于过切点的直径),而抛物线的切线虽然也容易用几何条件描述,但相关结论却难以用纯几何法证出。所以涉及切线问题时,还是需要用坐标法证明一个重要结论的。虽然如此,本文的证明过程还是要比带着一大坨方程的纯代数法清爽得多。
要证结论,得先给出定义:
定义 由平面内到一个定点和一条定直线距离相等的所有点构成的图形,称为抛物线. 定点称为抛物线的焦点,定直线称为抛物线的准线, 焦点到准线的距离称为焦准距.
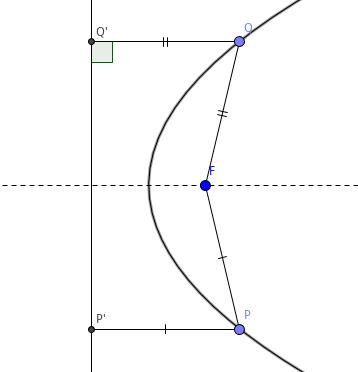
结论 1 抛物线是轴对称图形,准线过焦点的垂线是它的一条对称轴.
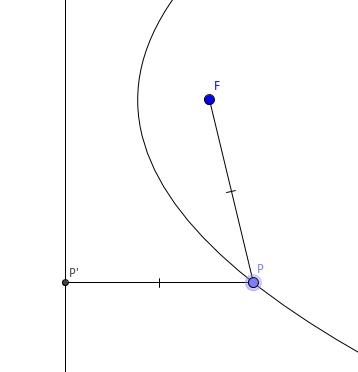
证明
设焦点为 \\(F\\), 准线为 \\(l\\), 轴为 \\(a\\), 抛物线上有一点 \\(P\\). 过 \\(P\\) 作 \\(PP\'\\perp l\\), 垂足为 \\(P\'\\). 当 \\(P\\) 不在 \\(a\\) 上时,作 \\(P\\) 关于 \\(a\\) 的对称点 \\(Q\\), 作 \\(P\'\\) 关于 \\(a\\) 的对称点 \\(Q\'\\). 连接 \\(FP\\)、\\(FQ\\). 由 \\(a \\perp l\\) 知 \\( PP\'\\parallel a \\), 所以 \\( QQ\'\\parallel a \\), 所以 \\(QQ\' \\perp l\\). 由对称知 \\(PP\'=QQ\'\\), \\(FP=FQ\\), 又 \\( FP=PP\' \\), 所以 \\( FQ=QQ\' \\), 所以 \\(Q\\) 在抛物线上, 结论得证.
定义 抛物线的准线过焦点的垂线称为抛物线的轴, 轴与抛物线的交点称为抛物线的顶点.
结论 2 设抛物线的焦点为 \\(F\\), 顶点为 \\(O\\), 焦准距为 \\(p\\), 对于抛物线上任意一点 \\(P\\), \\(FP = \\frac{p}{1+\\cos{\\angle{OFP}}}\\).
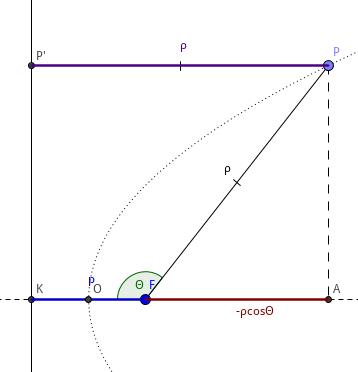
证明
设 \\(FP=\\rho\\), \\(\\angle{OFP}=\\theta\\).
如图,当 \\(\\theta > 90^{\\circ}\\) 时,作 \\(FP\\) 在轴上的投影,易得 \\(\\rho = p-\\rho\\cos{\\theta}\\). 整理得 \\(\\rho = \\frac{p}{1+\\cos{\\theta}}\\), 即 \\(FP = \\frac{p}{1+\\cos{\\angle{OFP}}}\\).
同理可证当 \\(0^{\\circ} < \\theta < 90^{\\circ}\\) 时,结论仍然成立.
当 \\(\\theta = 90^{\\circ}\\) 时,\\( PF=p \\), 结论仍然成立。
当 \\(\\theta = 0^{\\circ}\\) 时,\\( PF = \\frac{p}{2} \\), 结论仍然成立.
综上,对于抛物线上任意一点 \\(P\\), 结论成立.
推论 1 设抛物线的焦准距为 \\(p\\), 过抛物线焦点 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点,则有 \\(\\frac{1}{AF}+\\frac{1}{BF}=\\frac{2}{p}\\).
推论 2 设抛物线的顶点为 \\(O\\), 焦准距为 \\(p\\), \\(\\angle{OFP}=\\theta\\), 过抛物线焦点 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点,则有 \\(AB=\\frac{2p}{\\sin^2{\\theta}}\\).
结论 3 设抛物线轴与准线的交点为 \\(K\\), 过抛物线焦点 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点, 则轴平分 \\(\\angle{AKB}\\).
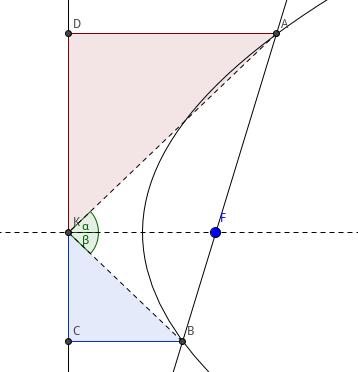
如图,设准线为 \\(l\\), 轴为 \\(a\\), 过 \\(A\\) 作 \\(AD\\perp l\\), 交 \\(l\\) 于 \\(D\\), 过 B 作 \\(BC\\perp l\\), 交 \\(l\\) 于 \\(C\\).
\\(\\because\\) \\(AD\\perp l\\) 且 \\(BC\\perp l\\)
\\(\\therefore\\) \\(AD\\parallel a\\) 且 \\(BC\\parallel a\\)
\\(\\therefore\\) \\(\\frac{KD}{KC}=\\frac{FA}{FB} \\)
又 \\(\\because\\) \\(FA=AD\\) 且 \\(FB=BC\\)
\\(\\therefore\\) \\(\\frac{KD}{KC}=\\frac{AD}{BC} \\)
\\(\\therefore\\) \\(\\triangle{KDA}\\sim \\triangle{KCB}\\)
\\(\\therefore\\) \\(\\angle{DKA} = \\angle{CKB}\\)
\\(\\therefore\\) 轴平分 \\(\\angle{AKB}\\)
结论 4 设抛物线焦点为 \\(F\\), 准线为 \\(l\\), 轴与准线的交点为 \\(K\\), 过 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点,过 \\(A\\) 作 \\(AD\\perp l\\), 交 \\(l\\) 于 \\(D\\), 过 B 作 \\(BC\\perp l\\), 交 \\(l\\) 于 \\(C\\), 则\\(FD\\) 平分 \\(\\angle{KFA}\\), \\(FC\\) 平分 \\(\\angle{KFB}\\), \\(FC\\perp FD\\).
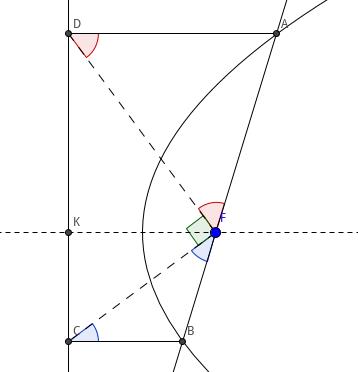
证明
\\(\\because\\) \\(FB=BC\\), \\(FA=AD\\)
\\(\\therefore\\) \\(\\angle{AFD}=\\angle{ADF}\\), \\(\\angle{BFC}=\\angle{BCF}\\)
\\(\\because\\) \\(KF\\parallel AD\\), \\(KF\\parallel BC\\)
\\(\\therefore\\) \\(\\angle{KFD}=\\angle{ADF}\\), \\(\\angle{KFC}=\\angle{FCB}\\)
\\(\\therefore\\) \\(FD\\) 平分 \\(\\angle{KFA}\\), \\(FC\\) 平分 \\(\\angle{KFB}\\)
\\(\\therefore\\) \\(FC\\perp FD\\)
结论 5 设抛物线焦点为 \\(F\\), 准线为 \\(l\\), 顶点为 \\(O\\), 过 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点,过 \\(A\\) 作 \\(AD\\perp l\\), 交 \\(l\\) 于 \\(D\\), 过 B 作 \\(BC\\perp l\\), 交 \\(l\\) 于 \\(C\\), 则 \\(A\\)、\\(O\\)、\\(C\\) 三点共线,\\(B\\)、\\(O\\)、\\(D\\) 三点共线.
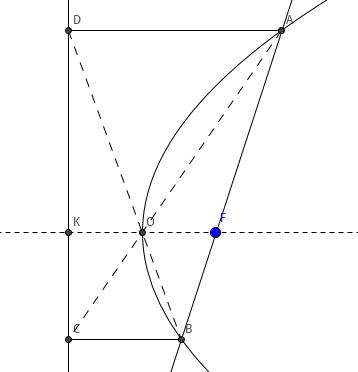
证明
连接 \\(AC\\) 交轴于 \\(O\'\\)
由 \\(\\triangle{AO\'F}\\sim \\triangle{ACB}\\) 得
\\( \\frac{BC}{O\'F}= \\frac{AB}{AF} \\)
\\( \\frac{BF}{O\'F}= \\frac{AF+BF}{AF} \\)
\\( \\frac{BF}{O\'F}= 1+\\frac{BF}{AF} \\)
\\( \\frac{1}{O\'F}= \\frac{1}{BF}+\\frac{1}{AF} \\)
由结论 2 推论 1 得
\\( \\frac{1}{O\'F}= \\frac{2}{p} \\)
\\( O\'F= \\frac{p}{2} \\)
\\( \\therefore \\) \\(O\'\\) 与 \\(O\\) 重合
\\( \\therefore \\) \\(A\\)、\\(O\\)、\\(C\\) 三点共线
同理可得 \\(B\\)、\\(O\\)、\\(D\\) 三点共线.
\\( \\therefore \\) 结论成立.
下面用坐标法证明抛物线切线的一个几何性质,作为描述抛物线切线的几何条件。
定理 在平面直角坐标系 \\(xOy\\) 中,焦点为 \\( (0, \\frac{p}{2}) \\), 准线为 \\( y=-\\frac{p}{2} \\) 的抛物线的方程为 \\( x^2=2py \\).
证明略.
结论 6 设抛物线顶点为 \\(O\\), 过顶点的切线为 \\(l\\), 抛物线上有一异于顶点的点 \\(P\\). 过点 P 作抛物线的切线 \\(m\\), 交 \\(l\\) 于 \\(M\\), \\(P\\) 在 \\(l\\) 上的投影为 \\(P\'\\), 则 \\(M\\) 是 \\(OP\\) 的中点.
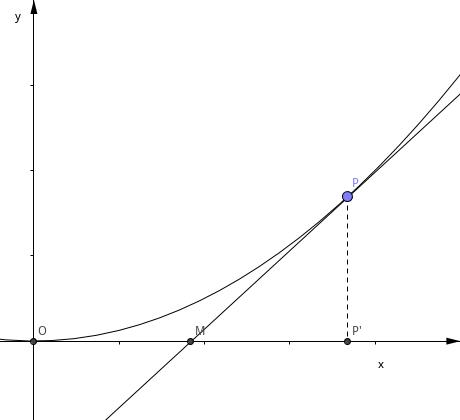
证明
如图建系. 设 \\( P(x_0, y_0) \\)
\\( y=\\frac{x^2}{2p} \\)
\\(\\Rightarrow y\'=\\frac{x}{p} \\)
\\(\\Rightarrow m: y-y_0 = \\frac{x_0}{p}(x-x_0)\\)
令 \\( y=0 \\), 得
\\( -y_0 = \\frac{x_0}{p}(x-x_0)\\)
解得
\\( x = \\frac{x_0}{2} \\)
\\( \\therefore \\) 结论得证
结论 7 设抛物线顶点为 \\(O\\), 焦点为 \\(F\\), 准线为 \\(l\\), 轴与准线的交点为 \\(K\\), 过顶点的切线为 \\(m\\), 抛物线上有一异于顶点的点 \\(P\\). 过点 \\(P\\) 作抛物线的切线 \\(t\\), 交 \\(m\\) 于 \\(M\\). 过 \\(P\\) 作 \\(PD\\perp l\\), 交 \\(l\\) 于 \\(D\\), 则 \\(F\\)、\\(D\\)、\\(M\\) 三点共线,切线 \\(PM\\) 是 \\(FD\\) 的垂直平分线.
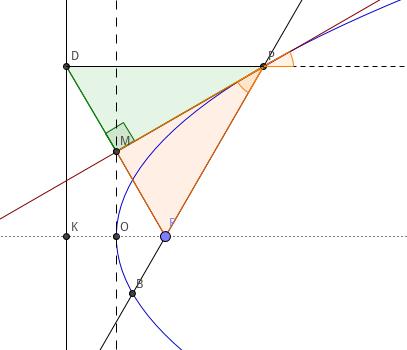
证明
由 \\(O\\) 是 \\(KF\\) 的中点及结论 6 可知,\\(F\\)、\\(D\\)、\\(M\\) 三点共线
\\( \\therefore \\) \\( DM=FM \\)
又 \\( \\because \\) \\( PF=PD \\), \\( MP=MP \\)
\\( \\therefore \\) \\( \\triangle{PMF}\\cong \\triangle{PMD} \\)
\\( \\therefore \\) \\(PM\\) 垂直平分 \\(FD\\)
\\( \\therefore \\) 结论得证
推论 从抛物线的焦点射出的光线,经抛物线反射后沿与抛物线的轴平行的方向射出.
结论 8 设抛物线焦点为 \\(F\\), 准线为 \\(l\\), 过顶点的切线为 \\(m\\), 过 \\(F\\) 的直线与抛物线交于 \\(A\\)、\\(B\\) 两点,过 \\(A\\) 作 \\(AD\\perp l\\), 交 \\(l\\) 于 \\(D\\), 过 B 作 \\(BC\\perp l\\), 交 \\(l\\) 于 \\(C\\), 过 \\(A\\)、\\(B\\) 作分别抛物线的切线 \\(t_1\\)、\\(t_2\\), \\( t_1\\cap m=G \\), \\( t_2\\cap m=H \\), 则 \\(t_1\\) 与 \\(t_2\\) 的交点 \\(T\\) 在 \\(l\\) 上,\\(TC=TD\\), 且 \\(TA\\perp TB\\).
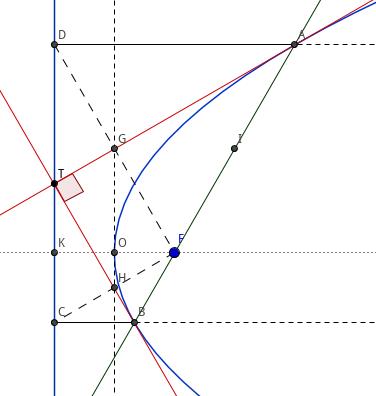
证明
设 \\( t_1\\cap l=T_1 \\), \\( t_2\\cap l=T_2 \\).
由结论 4 及 结论 7 知,\\(T_1G\\perp FD\\), \\(CF\\perp FD\\)
\\( \\therefore \\) \\(T_1G\\parallel CF\\)
又由结论 7 知,\\(G\\) 是 \\(FD\\) 的中点
\\( \\therefore \\) \\(T_1G\\) 是 \\(\\triangle{DFC}\\) 的中位线
\\( \\therefore \\) \\(T_1\\) 是 \\(CD\\) 的中点
同理可知,\\(T_2\\) 也是 \\(CD\\) 的中点
\\( \\therefore \\) \\(T_1\\) 与 \\(T_2\\) 重合
\\( \\therefore \\) \\(t_1\\) 与 \\(t_2\\) 在 \\(m\\) 上交于一点
设这一点为 \\(T\\).
由结论 4 及 结论 7 知,\\(\\angle{TGF}=\\angle{GFH}=\\angle{FHT}=90^{\\circ}\\)
\\( \\therefore \\) \\(\\angle{HTG}=90^{\\circ}\\)
\\( \\therefore \\) \\(TG\\perp TH\\), 即 \\(TA\\perp TB\\)
综上,结论得证.
推论 1 四边形 \\(TGFH\\) 是矩形.
推论 2 以 \\(AB\\) 为直径的圆与准线相切,以 \\(AF\\) 为直径的圆、以 \\(BF\\) 为直径的圆与 \\(m\\) 相切.
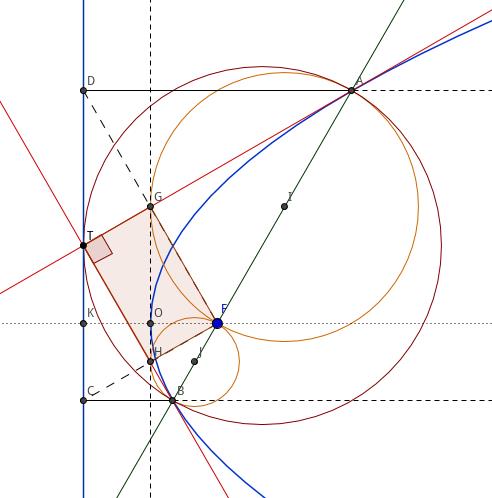
能想到的性质暂时就这么多。欢迎补充。
以上是关于抛物线的几何性质(传统几何法推导)的主要内容,如果未能解决你的问题,请参考以下文章