119. 杨辉三角 II

Posted 2020-11-29 lzh1043060917

 

https://leetcode-cn.com/problems/pascals-triangle-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--28/

 思路：

注意一下给出的用例，最上方节点算是第0行，所以说，第三行的这个3，是下标，所以说有四个元素

方法一：

和上题一样的算法，不过，最后res.get

class Solution {
    public List<Integer> getRow(int rowIndex) {//索引，等于索引加一层
    List<List<Integer>>  res=new ArrayList<List<Integer>>();
        List<Integer> a=new ArrayList<>(1);
        //看笔记！！！
        res.add(new ArrayList<>());
        res.get(0).add(1);//顶部元素一定是1
        if(rowIndex==0) return res.get(0);
        for(int j=1;j<rowIndex+1;j++)//遍历所有的层
        {
            List<Integer> row=new ArrayList<>();//当前层，当前是第几层，就有几个数字！！容易忘掉
            List<Integer> prerow=res.get(j-1);
            row.add(1);//每一行第一个数字为1
            for(int i=1;i<j;i++)//第j行最多j个元素，此行第n个元素等于上一行第n-1与n个元素之和
            {
                row.add(prerow.get(i)+prerow.get(i-1));//

            }
            row.add(1);//当前行最后一个元素
            res.add(row);

        }
        return res.get(rowIndex);
    }
}

　　方法2：

 

每次只保存上一层的结果就好

注意一下，因为参数其实是“下标”，比如说参数为3，求的其实是第四行，而且，下标为n时，这一行的List下标最多也就n个，比如第零行，下标0.第1行，下标0,1.。。。。。

class Solution {
    public List<Integer> getRow(int rowIndex) {
         List<Integer> pre = new ArrayList<>();
        List<Integer> cur = new ArrayList<>();
        for(int i=0;i<=rowIndex;i++)//第0行，下标最多为0，第3行，下标0,1,2,3
        {
            cur=new ArrayList<Integer>();//每一次循环，代表当前行的List都要更新一下，
            for(int j=0;j<=i;j++)
            {
               if (j == 0 || j == i) {
                cur.add(1);
            } else {
                cur.add(pre.get(j - 1) + pre.get(j));
            }  
            }
            pre=new ArrayList<>(cur);//更新当前行

        }
        return cur;
    }
}

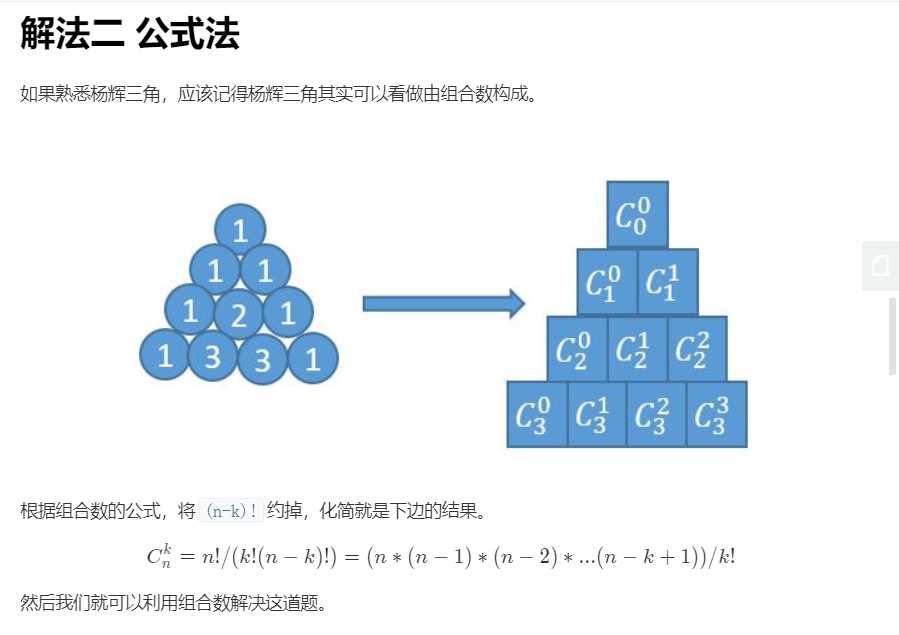
　　方法3：

 

 

public List<Integer> getRow(int rowIndex) {
    List<Integer> ans = new ArrayList<>();
    int N = rowIndex;
    for (int k = 0; k <= N; k++) {
        ans.add(Combination(N, k));
    }
    return ans;
}

private int Combination(int N, int k) {
    long res = 1;
    for (int i = 1; i <= k; i++)
        res = res * (N - k + i) / i;
    return (int) res;
}

作者：windliang
链接：https://leetcode-cn.com/problems/pascals-triangle-ii/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by--28/
来源：力扣（LeetCode）
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。