7-17 汉诺塔的非递归实现 (25分)

Posted 2020-11-28 2020r

一开始看见通过了0.4+，以为是送分题，结果我错了。

花了好长时间看博客没搞懂怎么非递归实现（菜……）。

后面看了

https://blog.csdn.net/computerme/article/details/18080511的算法和https://zhuanlan.zhihu.com/p/36085324的非递归实现方法受到启发才把代码给敲出来。

下面简单说一下我理解到的方法吧！

 

第一步是判断输入的n是奇数还是偶数，若为奇数，则按顺时针以ACB的顺序摆成品字型，若为偶数，则按顺时针以ABC的顺序摆成品字型。（参考下图）

 

 

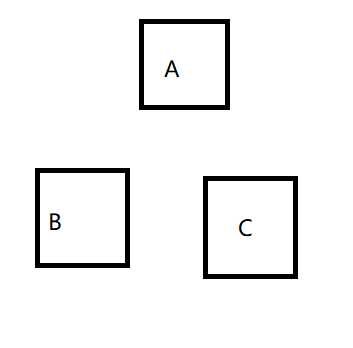
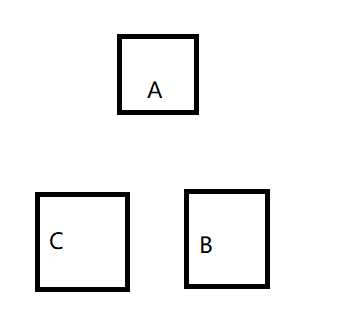
第二步将序号为1（最小）的盘，按顺时针放到下一个字母。假如以ABC顺序顺时针摆放时，若1盘在A，则将它移动到B，若在B则移动到C……

第三步处理剩余两个字母（1盘此时不在的那两个字母），暂且称为X和Y。可能会出现如下几种情况：

1）X和Y都有盘，此时他们顶层的盘必能比较出大小，那么这时候将小的盘移动到大的盘上面，结束。

 

2）X和Y都没盘，不用做任何处理。（比如输入的n为1的时候就会出现这种情况）

 

3）X和Y一个有盘，一个没盘，这时候将有盘的一边的盘移动到没有盘的一边，结束。

 

只要我们循环运行第二步和第三步就能完成汉诺塔的非递归实现啦。

下面是我的AC代码：

  1 //非递归AC代码
  2 //用cout最后一个测试会超时，改为printf就AC了
  3
  4 #include <iostream>
  5 #include <string>
  6 #include <cstring>
  7 #include <stdio.h>
  8 #include <cmath>
  9 using namespace std;
 10 int n;//输入的盘子数
 11 
 12 class stack_//“三根柱子”的类型
 13 {
 14 public:
 15     stack_() :r(0){}
 16     ~stack_() {}
 17     void push(int k)
 18     {
 19         h[++r] = k;
 20     }
 21     int pop()
 22     {
 23         if (r <= 0)
 24             return 0;
 25         else
 26         return h[r--];
 27     }
 28 public:
 29     char name;
 30     int r;//指针
 31     int h[10000];
 32 };
 33 stack_ S[3];//将三根柱子定义为数组，方便操作
 34 
 35 bool is_over(int cnt)//判断移动次数有没有超过2^n-1
 36 {
 37     if (cnt >= pow(2, n)-1)
 38         return true;
 39     else
 40         return false;
 41 }
 42 
 43 void move(char a, char b, char c)//移动函数主体
 44 {
 45     int pop_x,temp1,temp2;
 46     int cnt = 0;//累计移动的次数
 47     int i = 0;//循环的次数
 48     
 49     while(cnt < pow(2,n)-1 )//移动次数到达最大时就要退出循环，继续循环会导致错误
 50     {
 51         int k;//中间变量，简化式子
 52         pop_x = S[i % 3].pop();//随着i的变化，可以实现对S[0],S[1],S[2]轮回判断
 53         if (pop_x == 1)
 54         {
 55             k = i + 1;
 56             S[k % 3].push(1);
 57             if (!is_over(cnt))
 58             {
 59                  //cout << S[i % 3].name << " -> " << S[k% 3].name << endl;
 60                 printf("%c -> %c
", S[i % 3].name, S[k % 3].name);
 61                     cnt++;
 62             }
 63             temp1 = S[(k + 1) % 3].pop();
 64             temp2 = S[(k - 1) % 3].pop();
 65             if ((temp1 != 0 && temp2 != 0)&& (temp1 < temp2)  || temp2 == 0 and temp1 != 0)//temp1 移动到 temp2 的情况
 66             {
 67                 S[(k - 1) % 3].push(temp2);
 68                 S[(k - 1) % 3].push(temp1);
 69                 if (!is_over(cnt))
 70                 {
 71                     //cout << S[(k + 1) % 3].name << " -> " << S[(k - 1) % 3].name <<endl;
 72                     printf("%c -> %c
", S[(k+1) % 3].name, S[(k-1) % 3].name);
 73                     cnt++;
 74                 }
 75             
 76             }
 77             else if (temp1 == 0 && temp2 == 0)
 78             {
 79                 //不移动任何盘子，只要把刚刚出栈的元素重新压回去
 80                 S[(k + 1) % 3].push(temp1);
 81                 S[(k - 1) % 3].push(temp2);
 82             }
 83             else
 84             {
 85                 S[(k + 1) % 3].push(temp1);
 86                 S[(k + 1) % 3].push(temp2);
 87                 if (!is_over(cnt))
 88                 {
 89                     //cout << S[(k - 1) % 3].name << " -> " << S[(k + 1) % 3].name << endl;
 90                     printf("%c -> %c
", S[(k-1)% 3].name, S[(k+1) % 3].name);
 91                     cnt++;
 92                 }
 93             }
 94             i++;//注意在末尾将i的值加1，实现0，1，2的轮回
 95         }
 96         else
 97         {
 98             S[i % 3].push(pop_x);//不符合条件，重新压回栈
 99             i++;
100         }
101     }
102     //cout << endl << cnt << endl;
103 }
104 
105 
106 void hanoi(int n, char a, char b, char c)//接口
107 {
108     S[0].name = a,
109     S[1].name = b;
110     S[2].name = c;
111     for (int i = n; i >= 1; i--)//从大到小将盘子压入栈
112     {
113         S[0].push(i);
114     }
115        move(a, b, c);//调用move开始进行移动
116 }
117 
118 int main()
119 {
120    cin >> n;
121     if (n % 2 == 0)
122         hanoi(n, ‘a‘, ‘b‘, ‘c‘);//偶数的时候按abc顺序
123     else
124         hanoi(n, ‘a‘, ‘c‘, ‘b‘);//奇数的时候按acb顺序
125     return 0 ;
126 }

 

再附加个递归实现的：

 1 //递归实现
 2 #include <iostream>
 3 #include <string>
 4 #include <cstring>
 5 
 6 using namespace std;
 7 void hanoi(int n, char a, char b, char c)
 8 {
 9     if(n==1)
10     {
11         cout << a <<" -> " << c << endl;
12         return;
13     }
14     else
15     {
16         hanoi(n-1,a,c,b);
17         cout << a <<" -> " << c <<endl;
18         hanoi(n-1,b,a,c);
19         return;
20     }
21 }
22 
23 int main()
24 {
25     int n ;
26     cin >> n;
27     hanoi(n,‘a‘,‘b‘,‘c‘);
28     return 0;
29 }

对于递归算法我的个人理解：
首先将初始盘子看成是n-1的整体和最下面的最大一块的组合体。

hanoi(n-1,a,c,b);
cout << a <<" -> " << c <<endl;
hanoi(n-1,b,a,c);

hanoi(n,A,B,C,)中A为初始位置，C为目标位置，上述代码第一步目的是将n-1整体从A移动到B,所以调用hanoi(n-1,A,C,B)。依此类推，第二步是要把最大一块从A移动到C，所以也可写成hanoi(1,A,B,C)，第三步同理。

 那么为什么hanoi(n-1,A,B,C)可以实现将上面的n-1个盘从A移动到B呢？

我的理解：

当n=2时，即n-1为1的时候，这个函数显然是可以实现这一目标的。当n=3时n-1就为2了，这个时候调用hanoi(n-1,A,B,C)其实就是调用hanoi(2,A,B,C)，那么我们刚刚已经确定参数为2的时候是可以达到目的的，那么可以推出，n为3的时候也可以达到目的（因为他是借助n-1=2时的函数实现的），于是就可以继续往后面推断出n为任何数字的时候都可以实现这一功能。