算法常识——结构与复杂度

Posted 2020-11-25 aoximin

前言

最一些算法基础的整理。

很多人提到算法就会涉及到数据结构。
个人理解之所以有数据结构是因为存储这个问题。
程序无论是读取硬盘还是内存，涉及到如何读取，读取问题呢，相当于找。那么如何能够快速的找到？关键在于当时我们怎么放，如何存放就是数据结构。
常见的数据结构：线，树，图。
个人理解，线是一维概念，图和树都是二维概念，当然还有三维概念，暂时不理解。
什么是算法？1+1等于2，算不算？
个人理解，算。实际上1+1等于2，并不简单，具体可参考计算机是如何计算的，而这个算法奠定了计算机基础。
符合下面的就属于算法:
一个算法应该具有以下五个重要的特征：
有穷性
（Finiteness）
算法的有穷性是指算法必须能在执行有限个步骤之后终止；
确切性
(Definiteness)
算法的每一步骤必须有确切的定义；
输入项
(Input)
一个算法有0个或多个输入，以刻画运算对象的初始情况，所谓0个输入是指算法本身定出了初始条件；
输出项
(Output)
一个算法有一个或多个输出，以反映对输入数据加工后的结果。没有输出的算法是毫无意义的；
可行性
(Effectiveness)
算法中执行的任何计算步骤都是可以被分解为基本的可执行的操作步骤，即每个计算步骤都可以在有限时间内完成（也称之为有效性）。

空间复杂度与时间复杂度

很多时候都听说过空间换时间，时间换空间，两者在最优的情况下是不可兼容的，在现在硬件的发展下，很多都选择空间换时间。

什么是时间复杂度？

时间复杂度计算有多种，其中一种为渐进时间复杂度。
因为电脑其实没有时间这个概念，即使是我们的电脑里面设置时间，也是通过无数次的无意义循序形成的，所以计算机中计算时间的就是执行的次数。

T(n)=100n; T(n)=5(n^2)

到底哪个最快？根据上述得到的结果为n。

渐进时间复杂度的概念：若存在函数f(n),T(n)/f(n)的极限值为不等于0的常数，则称f(n)是T(n)的同级函数。记作T(n)=o(f(n))0,o为算法的渐进时间的复杂度，简称时间复杂度。

这个是什么意思？

1.如果运行时间是常亮级则为1

2.只保留函数最高阶

3.如果最高阶项存在，则省去最高阶前面的系数。

说了这么多什么意思呢？

比如说 5n^2+2n+6

就是把常亮为1：n^2 +n +1

保留最高阶:n^2

这就是时间复杂度了。

举例:
执行次数为线性:n

public void test1(int n)
{
    for (int i = 0; i < n; i++) {
        Console.WriteLine("do the timer:"+i);
    }
}

对数:log(n)

int sum = 0;
for (int i = n; i > 1; i /= 2)
{
    Console.WriteLine("do the timer:"+(++sum));
}

常数1:

Console.WriteLine("do the timer:"+(++sum));

0.5n^2+0.5 根据前面的原则，为n^2

for (int i = 0; i < n; i++)
{
    for (int j = 0; j < i; j++)
    {
        Console.WriteLine("do the timer:" + (++sum));
    }
}

空间复杂度：

时间复杂度可以通过执行次数计算，那么空间呢？
空间计算没有我们想象的那么简单，因为在执行输入的时候我们需要向系统申请空间，比如for 循环的i。
空间复杂度：对一个算法都在运行过程中临时用到的空间。
比如说:
我们在比较大小的时候会用到temp，那么复杂度就为0(1)

void space1()
{
    int temp = 0;
}

线性空间:o(n)

void space1(n)
{
    int[] temp = new int[n];
}

我们计算矩阵的时候用到的:
n^2

void space1(n)
{
    int[][] temp = new int[n][n];
}

4.递归空间

递归空间就是一个特殊的例子:

void space2(int n)
{
    if (n <= 1)
    {
        return;
    }
    space2(n);
}

这时候n就是临时变量，这里面n的次数就为n，所以为o(n)
如果是:

void space2(int n)
{
    if (n <= 1)
    {
        return;
    }
    space2(n/2);
}

那么就是o(n)=log(n)。
也就是说也需要计算n的临时变量次数。

空间和时间如何取舍

举个空间换时间的方法:

下面例子来自漫画算法这本书:

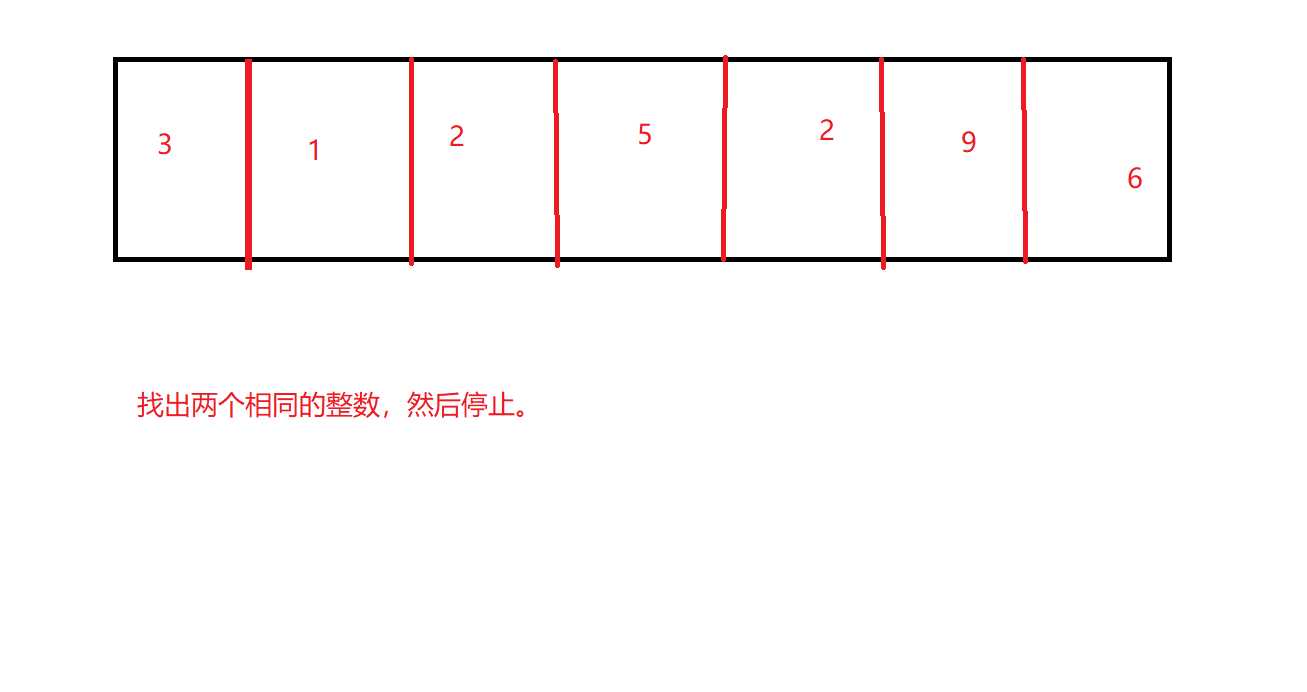
上述就是题目了，最简单的方式就是从3开始，然后遍历后面的，然后1，遍历后面的。

根据输入的个数，复杂度为:0.5n^2+0.5n,时间复杂度为o(n^2)

那么如何加一个字典来记录:

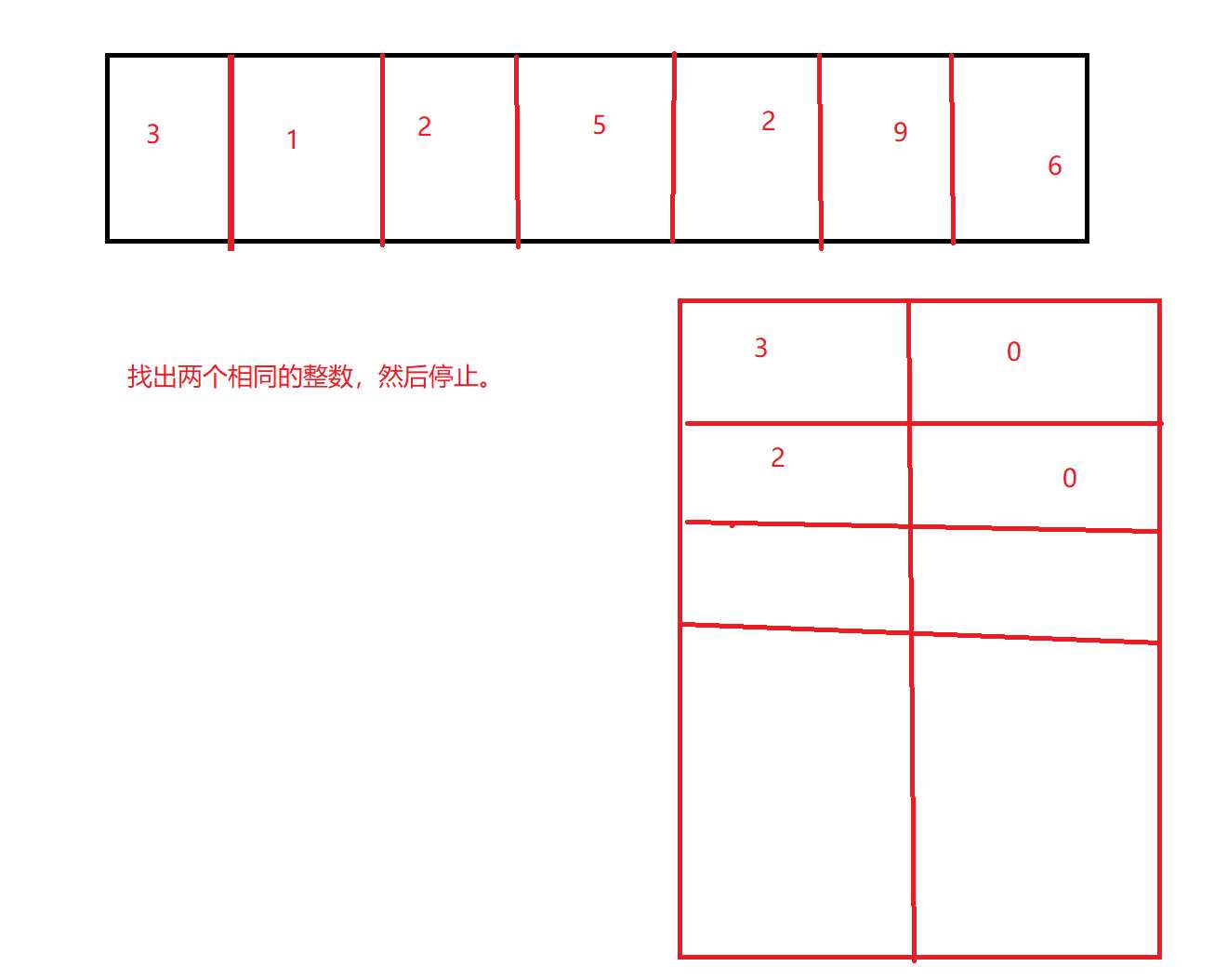
如果为0，那么就设置为1，如果为1就说明以前存在，那么就跳出。
因为只遍历一遍，查询字典的时间复杂度为o(1)，所以时间复杂度为o(n),空间复杂度也为o(n)。
其实这就很假了，因为创建一个字典本身需要花费时间，人类无法计算出全部的计算，所以只能设定为n在极限情况下，具体还要看程序本身，需要经过测试，经验。