算法常识——非线性结构

Posted 2021-03-13 aoximin

前言

非线性结构是相当线性结构而言的。
线性结构是一个有序数据元素的集合。
下述来自百度百科:

1．集合中必存在唯一的一个"第一个元素"；
2．集合中必存在唯一的一个"最后的元素"；
3．除最后元素之外，其它数据元素均有唯一的"后继"；
4．除第一元素之外，其它数据元素均有唯一的"前驱"。
数据结构中线性结构指的是数据元素之间存在着“一对一”的线性关系的数据结构。
如（a0,a1,a2,.....,an）,a0为第一个元素，an为最后一个元素，此集合即为一个线性结构的集合。
相对应于线性结构，非线性结构的逻辑特征是一个结点元素可能对应多个直接前驱和多个后继。

正文

在非线性结构中常用的:有树和图。

树

树的数据结构是怎么样的？

人们把这种分叉的东西，看起来像树一样，就称作树。其实这一点也不像树，毕竟树根在下面，总之这个称作树的人，可以吹好久的牛了。
树的概念:
树是n(n>=0)个节点的有限集合。当n=0时，称为空树。在任意一个非空树中，有如下特点:
1.有且仅有一个特定的称为根的节点。
2.当n>1时，其余节点可分为m(m>0)个互不橡胶的有限集，每个集合本身又是一个树，称为子树。
下面是一些概念性东西：
根节点：只有一个，第一个元素。
叶子节点：后面没有节点。
子树：设T是有根树，a是T中的一个顶点，由a以及a的所有后裔（后代）导出的子图称为有向树T的子树。
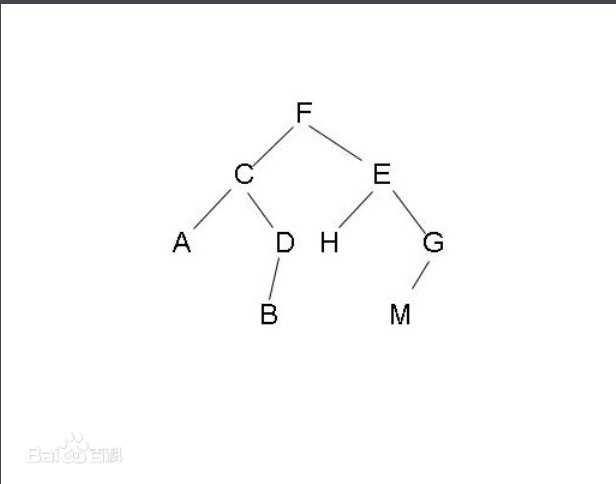
如下图:

父节点:是其子节点的父节点。
子节点：相对其父节点是子节点。
兄弟节点：同一个父节点。

二叉树

可以说二叉树是玩花样最多的东西，为什么这么说？
因为二叉树有规律性可寻，有穷，特点多，有成为各种算法的潜质。
二叉树如图:

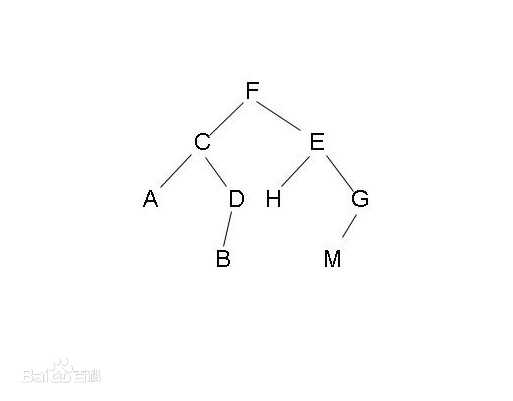
查看一下概念：
首先要符合树，这种树的每一个节点最多有2个孩子阶段。左边的称为：左孩子，右边的称为右孩子。
特殊的二叉树:

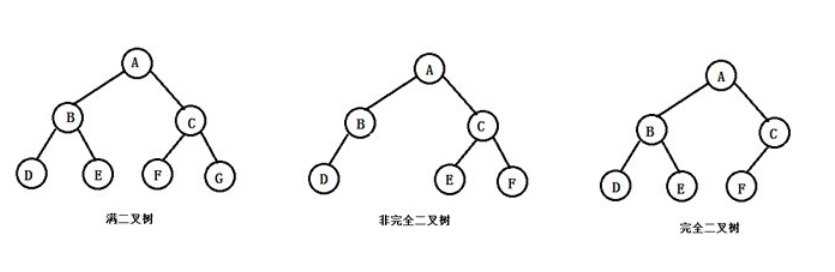
1.满二叉树:
一个二叉树的所有的非叶子节点都存在左右孩子，并且所有的叶子节点都在同一层级上，并且这个树就是满二叉树。
完全二叉树:对于一个有n个节点的二叉树，按层级顺序编号，则所有节点的便函为1到n，如果这个树所有节点和同意的满二叉树的编号为从1到n的节点位置相同，则这个二叉树为完全二叉树。

存储

在前面提及到逻辑概念之所以是逻辑概念，是因为其一定要基于物理概念，物理结构可以多样，就像做门可以用不同材料。
假如说用顺序存储的数组来存取。
比如说下方这个:

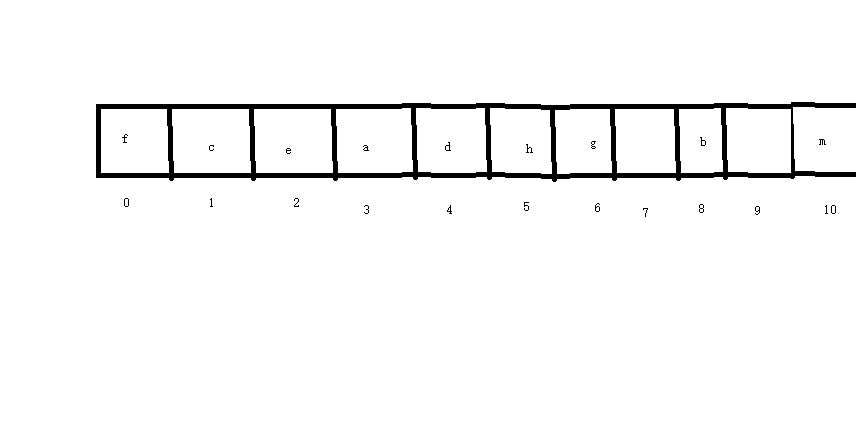
然后数组存储如下：

从左往右，记录其子节点，没有的不存。
有个规律之处在于：
其父节点与左孩子节点的左边位置关系:
父节点索引位为:parent
左孩子为2parent+1
这是怎么算过来的？假设父节点在第n层，那么最后一个元素的索引为2^0+2^1+....+2^n-1,减1是因为从0开始,那么是2^(n+1)-2，假设父元素距离最后一个位置为x，那么父元素索引为2^(n+1)-2-x
左孩子一定是在n+1层,同理n+1层最后一个元素是2^(n+2)-2，因为父元素距离n层最后一个元素为x，那么左子元素一定距离为2x+1，2^(n+2)-2-(2x-1)。
2^(n+2)-2-(2x-1)=2（2^(n+1)-2-x）+1。
所以结论就是：2parent+2
同理右节点就是左节点加1为:2*parent+2
当然如何很稀疏的话太浪费空间。