算法——二分搜索树
Posted cxc1357
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了算法——二分搜索树相关的知识,希望对你有一定的参考价值。
- 二叉树,每个节点键值大于左孩子,小于右孩子
- 和堆的区别,不一定是完全二叉树
- 可使用递归实现
- 存储键值对,可高效地实现插入、查找、删除
查找 插入 删除
普通数组 O(n) O(n) O(n)
顺序数组 O(logn) O(n) O(n)
二分搜索树 O(logn) O(logn) O(logn)
- 遍历
- 深度优先:前/中/后序(递归)
- 广度优先:层序遍历(队列)
- 删除
- 删除最大/小值所在节点
- 删除任意节点
- 只有左/右孩子
- 左、右孩子都有(Hibbard Deletion)
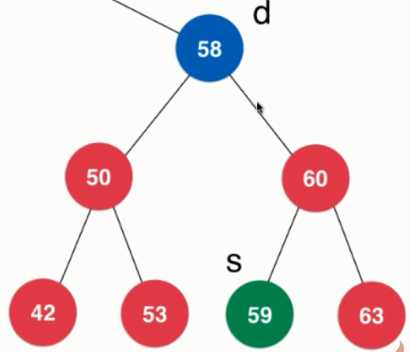
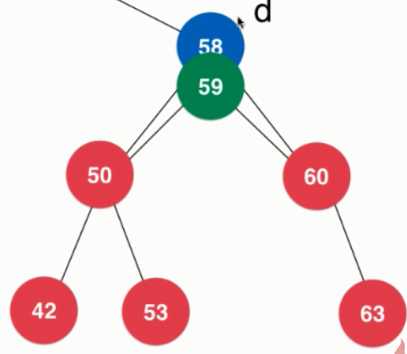
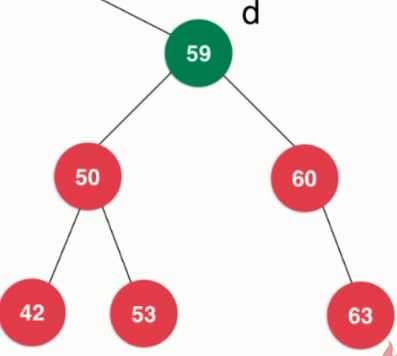

- 顺序性
- 前驱
- 后继
- floor:最接近且小于
- ceil:最接近且大于
- rank:某元素的排名
- select:排名第x的元素是谁
- 支持重复元素:node结构体增加一个属性count
- 局限性
- 同样的数据可以对应不同的二分搜索树,极端情况退化为链表
- 平衡二叉树:2-3树、AVL树、伸展树、红黑树
- Treap:平衡二叉树和堆的结合
- trie:按字母顺序存储单词
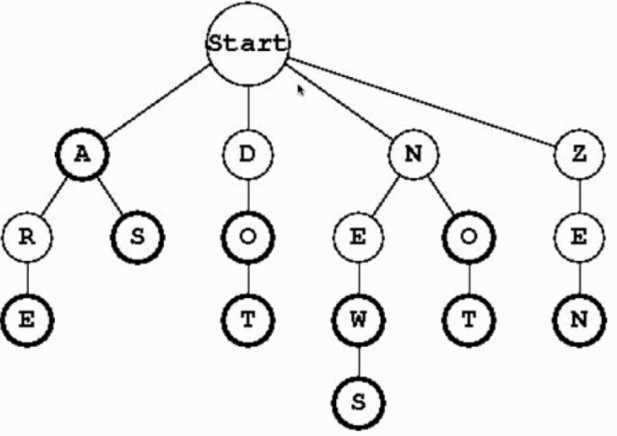
- 树形问题:用树解决问题,但没有创建具体的树
- 排序:归并排序、快速排序(都采用递归实现,类似二叉搜索树的后序遍历)
- 搜索:决策树、8数码、华容道、数独、搬运工、深蓝
main.cpp

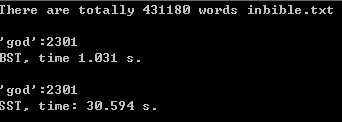
1 #include <iostream> 2 #include <vector> 3 #include <string> 4 #include <ctime> 5 #include "SequenceST.h" 6 #include "FileOps.h" 7 #include "BST.h" 8 9 using namespace std; 10 11 int main(){ 12 string filename = "bible.txt"; 13 vector<string> words; 14 if( FileOps::readFile(filename, words)){ 15 cout << "There are totally " << words.size() << " words in" << filename << endl; 16 cout << endl; 17 18 // 测试BST 19 // 统计所有词的词频 20 time_t startTime = clock(); 21 BST<string, int> bst = BST<string, int>(); 22 for(vector<string>::iterator iter = words.begin();iter != words.end(); iter++ ){ 23 int *res = bst.search(*iter); 24 if(res == NULL) 25 bst.insert(*iter, 1); 26 else 27 (*res)++; 28 } 29 // 输出god一词的词频 30 if(bst.contain("god")) 31 cout << "‘god‘:" << *bst.search("god") << endl; 32 else 33 cout << "No word ‘god‘ in " << filename << endl; 34 time_t endTime = clock(); 35 cout << "BST, time " << double(endTime - startTime)/CLOCKS_PER_SEC << " s." << endl; 36 cout << endl; 37 38 // 测试顺序查找表 39 startTime = clock(); 40 // 统计所有词的词频 41 SequenceST<string, int> sst = SequenceST<string, int>(); 42 for(vector<string>::iterator iter = words.begin(); iter != words.end();iter++){ 43 int *res = sst.search(*iter); 44 if(res == NULL) 45 sst.insert(*iter, 1); 46 else 47 (*res)++; 48 } 49 // 输出god一词的词频 50 if(sst.contain("god")) 51 cout << "‘god‘:" << *sst.search("god") << endl; 52 else 53 cout << "No word ‘god‘ in " << filename << endl; 54 endTime = clock(); 55 cout << "SST, time: " << double(endTime - startTime)/CLOCKS_PER_SEC << " s." << endl; 56 } 57 return 0; 58 }
BST.h

1 #include <iostream> 2 #include <queue> 3 #include <cassert> 4 5 using namespace std; 6 7 template <typename Key, typename Value> 8 class BST{ 9 private: 10 struct Node{ 11 Key key; 12 Value value; 13 Node *left; 14 Node *right; 15 16 Node(Key key, Value value){ 17 this->key = key; 18 this->value = value; 19 this->left = this->right = NULL; 20 } 21 Node(Node *node){ 22 this->key = node->key; 23 this->value = node->value; 24 this->left = node->left; 25 this->right = node->right; 26 } 27 }; 28 Node *root; 29 int count; 30 public: 31 BST(){ 32 root = NULL; 33 count = 0; 34 } 35 ~BST(){ 36 destroy( root ); 37 } 38 int size(){ 39 return count; 40 } 41 bool isEmpty(){ 42 return count == 0; 43 } 44 void insert(Key key, Value value){ 45 root = insert(root, key, value); 46 } 47 bool contain(Key key){ 48 return contain(root, key); 49 } 50 // 若返回Node*需把Node结构体定义为public 51 // 返回值,则外界不知道Node结构体的存在,实现了封装 52 Value* search(Key key){ 53 return search( root, key); 54 } 55 void preOrder(){ 56 preOrder(root); 57 } 58 void inOrder(){ 59 inOrder(root); 60 } 61 void postOrder(){ 62 postOrder(root); 63 } 64 // 层序遍历 65 void levelOrder(){ 66 queue<Node*> q; 67 q.push(root); 68 while( !q.empty() ){ 69 Node *node = q.front(); 70 q.pop(); 71 cout << node->key << endl; 72 if( node->left ) 73 q.push( node->left ); 74 if( node->right ) 75 q.push( node->right ); 76 } 77 } 78 // 寻找最小键值 79 Key minimum(){ 80 assert( count != 0 ); 81 Node* minNOde = minimum( root ); 82 return minNode -> key; 83 } 84 // 寻找最大键值 85 Key maximum(){ 86 assert( count != 0 ); 87 Node* maxNode = maximum( root ); 88 return maxNode -> key; 89 } 90 // 删除最小值所在节点 91 // 从根节点开始,寻找最小值节点并将其删除 92 void removeMin(){ 93 // 根为空才运行 94 if( root ) 95 // 删除以root为根的二分搜索树的最小节点 96 // 并传回新的根 97 root = removeMin( root ); 98 } 99 // 删除最大值所在节点 100 void removeMax(){ 101 if( root ) 102 root = removeMax( root ); 103 } 104 // 从二叉树中删除键值为key的节点 105 // O(Olog),用于找到节点,指针间的交换为常数级 106 void remove(Key key){ 107 root = remove(root, key); 108 } 109 110 private: 111 // 向以node为根的二叉搜索树中,插入节点(key,value) 112 Node* insert(Node *node, Key key, Value value){ 113 if( node == NULL ){ 114 count ++; 115 return new Node(key, value); 116 } 117 if( key == node->key ) 118 node->value = value; 119 else if( key < node->key ) 120 node->left = insert( node->left, key, value); 121 else 122 node->right = insert( node->right, key, value); 123 return node; 124 } 125 // 查看以node为根的二叉搜索树中是否包含键值为key的节点 126 bool contain(Node* node, Key key){ 127 if( node == NULL ) 128 return false; 129 if( key == node->key ) 130 return true; 131 else if( key < node->key ) 132 return contain( node->left, key ); 133 else 134 return contain( node->right, key); 135 } 136 // 在以node为根的二叉搜索树中查找key对应的value 137 Value* search(Node* node, Key key){ 138 if( node == NULL ) 139 return NULL; 140 if( key == node->key ) 141 return &(node->value); 142 else if( key < node->key ) 143 return search( node->left, key ); 144 else 145 return search( node->right, key); 146 } 147 // 对以node为根的二叉搜索树进行前序遍历 148 void preOrder(Node* node){ 149 if( node != NULL ){ 150 cout << node->key << endl; 151 preOrder(node->left); 152 preOrder(node->right); 153 } 154 } 155 // 对以node为根的二叉搜索树进行中序遍历 156 void inOrder(Node* node){ 157 if( node != NULL ){ 158 inOrder(node->left); 159 cout << node->key << endl; 160 inOrder(node->right); 161 } 162 } 163 // 对以node为根的二叉搜索树进行后序遍历 164 void postOrder(Node* node){ 165 if( node != NULL ){ 166 postOrder(node->left); 167 postOrder(node->right); 168 cout << node->key << endl; 169 } 170 } 171 // 后序遍历删除节点 172 void destroy(Node* node){ 173 if( node != NULL){ 174 destroy( node->left); 175 destroy( node->right); 176 delete node; 177 count --; 178 } 179 } 180 // 在以node为根的二叉搜索树中,返回最小键值的节点 181 Node* minimum(Node* node){ 182 if( node->left == NULL ) 183 return node; 184 return minimum(node->left); 185 } 186 // 在以node为根的二叉搜索树中,返回最大键值的节点 187 Node* maximum(Node* node){ 188 if( node->right == NULL ) 189 return node; 190 return maximum(node->right); 191 } 192 // 删除以node为根的二分搜索树中的最小节点 193 // 递归到左子树的最左侧节点 194 // 删除该节点,再把右子树接到父节点上 195 // 返回删除节点后新的二分搜索树的根 196 // 因为要递归调用,参数和返回值要一致 197 Node* removeMin(Node* node){ 198 // 找到最小节点 199 if( node->left == NULL){ 200 Node* rightNode = node->right; 201 delete node; 202 count --; 203 return rightNode; 204 } 205 node->left = removeMin(node->left); 206 return node; 207 } 208 // 删除以node为根的二分搜索树中的最大节点 209 // 返回删除节点后新的二分搜索树的根 210 Node* removeMax(Node* node){ 211 if( node->right == NULL){ 212 Node* leftNode = node->left; 213 delete node; 214 count --; 215 return leftNode; 216 } 217 node->right = removeMax(node->right); 218 return node; 219 } 220 221 Node* remove(Node* node, Key key){ 222 if( node == NULL ) 223 return NULL; 224 if( key < node->key ){ 225 node->left = remove( node->left, key ); 226 return node; 227 } 228 else if( key > node->key ){ 229 node->right = remove( node->right, key ); 230 return node; 231 } 232 else{ // key == node->key 233 if( node->left = NULL ){ 234 Node* rightNode = node->right; 235 delete node; 236 count --; 237 return rightNode; 238 } 239 if( node->right = NULL ){ 240 Node* leftNode = node->left; 241 delete node; 242 count --; 243 return leftNode; 244 } 245 // node->left != NULL && node->right != NULL 246 Node *delNode = node; 247 Node *successor = new Node(minimun(node->right)); 248 count ++; 249 successor->right = removeMin(node->right); 250 successor->left = node->left; 251 delete delNode; 252 count --; 253 return successor; 254 } 255 } 256 };
SequenceST.h

1 #include<iostream> 2 #include<cassert> 3 4 using namespace std; 5 6 template<typename Key, typename Value> 7 class SequenceST{ 8 private: 9 struct Node{ 10 Key key; 11 Value value; 12 Node *next; 13 14 Node(Key key, Value value){ 15 this->key = key; 16 this->value = value; 17 this->next = NULL; 18 } 19 }; 20 Node* head; 21 int count; 22 23 public: 24 SequenceST(){ 25 head = NULL; 26 count = 0; 27 } 28 ~SequenceST(){ 29 while( head != NULL){ 30 Node *node = head; 31 head = head->next; 32 delete node; 33 count --; 34 } 35 assert( head == NULL && count == 0 ); 36 } 37 int size(){ 38 return count; 39 } 40 bool isEmpty(){ 41 return count == 0; 42 } 43 void insert(Key key, Value value){ 44 Node *node = head; 45 // 若表中有同样大小的key则更新value 46 while( node != NULL){ 47 if( key == node->key ){ 48 node->value = value; 49 return; 50 } 51 node = node->next; 52 } 53 // 若表中无同样大小的key则在表头创建新节点 54 Node *newNode = new Node(key, value); 55 newNode->next = head; 56 head = newNode; 57 count ++; 58 } 59 60 61 //顺序表中是否包含键值为key的节点 62 bool contain(Key key){ 63 Node *node = head; 64 while( node != NULL){ 65 if( key == node->key ) 66 return true; 67 node = node->next; 68 } 69 return false; 70 } 71 72 //查找key对应的value 73 Value* search(Key key){ 74 Node *node = head; 75 while( node != NULL){ 76 if( key == node->key ) 77 return &(node->value); 78 node = node->next; 79 } 80 return NULL; 81 } 82 // 删除(key,value)节点 83 void remove(Key key){ 84 // 头节点需特殊处理 85 if( key == head->key ){ 86 Node* delNode = head; 87 head = head->next; 88 delete delNode; 89 count--; 90 return; 91 } 92 Node* node = head; 93 while( node->next != NULL && node->next->key != key) 94 node = node->next; 95 if(node->next!=NULL){ 96 Node* delNode = node->next; 97 node->next = delNode->next; 98 delete delNode; 99 count--; 100 return; 101 } 102 } 103 };
FileOps.h

1 #include <string> 2 #include <iostream> 3 #include <fstream> 4 #include <vector> 5 6 using namespace std; 7 8 namespace FileOps{ 9 // 定位字母 10 int firstCharacterIndex(const string& s, int start){ 11 for( int i = start ; i < s.length() ; i ++ ) 12 if( isalpha(s[i]) ) 13 return i; 14 return s.length(); 15 } 16 17 // 将字符串s中的所有字母转换成小写后返回 18 string lowerS( const string& s){ 19 string ret = ""; 20 for( int i = 0 ; i < s.length() ; i ++ ) 21 ret += tolower(s[i]); 22 return ret; 23 } 24 25 // 读取filename中的内容,并将其中包含的词语放进words 26 bool readFile(const string& filename, vector<string> &words){ 27 string line; 28 string contents = ""; 29 ifstream file(filename); 30 if( file.is_open() ){ 31 while( getline(file,line) ) 32 contents += (line + " "); 33 file.close(); 34 } 35 else{ 36 cout << "Can not open "<<filename<<" !!!"<<endl; 37 return false; 38 } 39 // 分词操作 40 // 定位第一个字母,然后定位这个字符以后第一个非字母的位置 41 // start:字母位置;i:对于start,之后第一个非字母的位置 42 int start = firstCharacterIndex(contents, 0); 43 for( int i = start + 1 ; i <= contents.length() ; ) 44 if( i == contents.length() || !isalpha(contents[i])){ 45 words.push_back( lowerS( contents.substr(start,i-start))); 46 start = firstCharacterIndex(contents,i); 47 i = start + 1; 48 } 49 else 50 i ++; 51 return true; 52 } 53 }
以上是关于算法——二分搜索树的主要内容,如果未能解决你的问题,请参考以下文章
学习数据结构笔记(11) --- [二分搜索树(BinarySearchtTree)]
挖掘算法中的数据结构:二分查找 和 二分搜索树(插入查找深度优先遍历)
c_cpp 二分搜索是所有以比较为基础的搜索算法时间复杂度最低的算法。用二叉树描速二分查找算法,最坏情况下与二叉树的最高阶相同。比较二叉树线性查找也可用二叉树表示,最坏情况下比较次数为数组元素数量。任
