学习数据结构笔记(11) --- [二分搜索树(BinarySearchtTree)]
Posted 小智RE0
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了学习数据结构笔记(11) --- [二分搜索树(BinarySearchtTree)]相关的知识,希望对你有一定的参考价值。
B站学习传送门–>尚硅谷Java数据结构与java算法(Java数据结构与算法)
1.二分搜索树
前面已经学习过二叉树,赫夫曼树的知识了;接下来学习二分搜索树的知识;
我们知道二叉树的结构就是父节点挂接左右子节点;二分搜索树的首先是个二叉树;然后融合了二分搜索的思想;
二分搜索树又称为二分排序树; 这种树的特点是,它的左子树上挂接的节点是小于根结点的; 右子树上挂接的节点是大于根结点的;属于是两级分化了;然后;若是相同的节点,放在左子节点或者右子节点都可以;
最大的节点就是最右边的节点;最小的节点就是最左边的节点;
比如下图中的树就是一棵二分搜索树
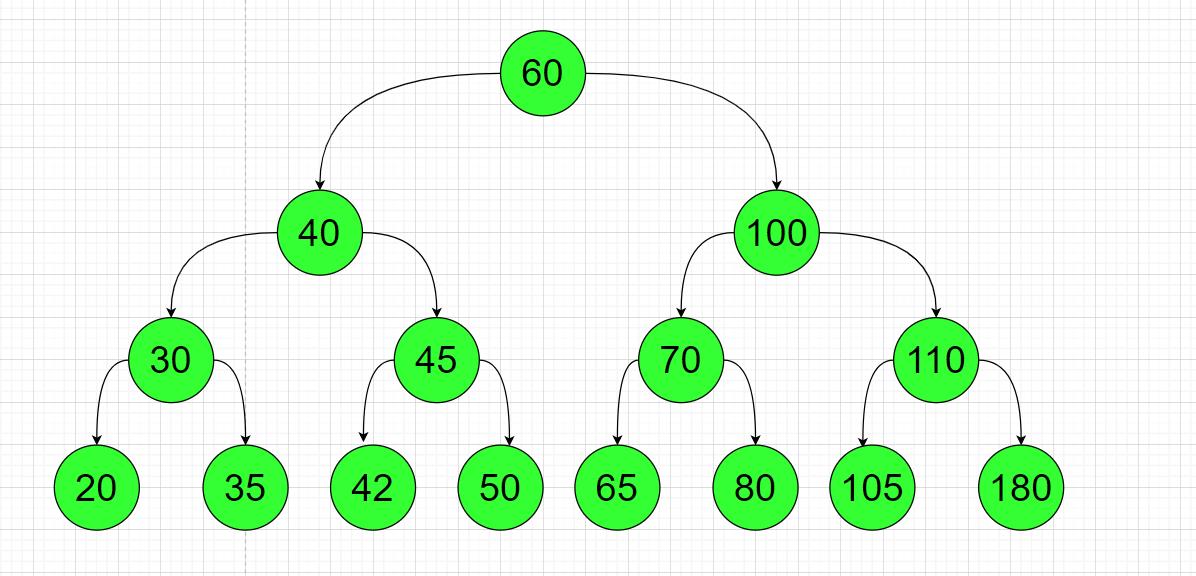
2.创建二分搜索树,以及添加节点的方法
在添加时,若是第一次添加,则将这个结点作为根结点;
在后续添加节点时,先和根结点比较,若小于等于根结点,就让它放到根节点的左子节点位置,若此时左子节点的位置已经有节点了,就把这个结点向左子节点下递归,若此时左子节点的位置没有节点;就直接把这个结点存放到左子节点位置;
若和根结点比较时,大于根结点,就把这个添加节点考虑根结点的右子节点位置;若右子节点已经有节点了,那就在右子节点向下递归;
图解过程
比如现在刚添加了第一个节点
50,那么就让它作为根节点;
第二个节点80准备添加,比较;大于根结点50,则让它挂接到根结点50的右子节点;
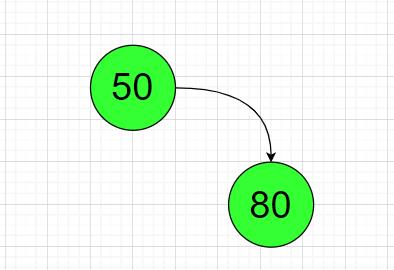
第三个节点
30准备添加,比较根结点50后,它小于根节点50,则让它挂接到根结点的左子节点;

第四个节点
8000准备添加,比较根结点后,它大于50;则准备挂接到根结点的右子节点,但是此时右子节点已经有节点80了,则此时递归让80作为一个比较节点;8000和80比较后,发现它大于当前的父节点,则让8000挂接到80的右子节点位置

第五个节点10考虑添加;和50比较之后,它小于50,则放置到50的左子节点;但是左子节点已经有节点30;则让这个结点递归;和节点30进行比较,挂接到节点30的左子节点位置;

具体实现
//二分搜索树;
class BSTree
//根节点;
private TreeNode root;
//在二分搜索树添加节点;
public void addNode(TreeNode node)
//若根结点为空,则让新添加的第一个节点暂时作为根结点;
if(root==null) root = node;
else
root.addNode(node);
//中序遍历二分搜索树;
public void infixList()
if(root==null)
throw new RuntimeException("the tree is empty");
root.infixList();
//节点
class TreeNode
//左节点,右节点;节点值;
TreeNode leftNode;
TreeNode rightNode;
int val;
//初始化节点;
public TreeNode(int val)
this.val = val;
@Override
public String toString()
return "TreeNode" + "val=" + val + '';
//添加节点的底层方法;
public void addNode(TreeNode node)
//先判断当前的节点是否为空;
if (node == null) return;
if (node.val <= this.val)
//考虑挂到左子节点;若左节点已经有了,则向左继续递归;
if (this.leftNode == null)
this.leftNode = node;
else
this.leftNode.addNode(node);
else
//右子节点;若有节点已经存在,则向右继续递归;
if(this.rightNode == null)
this.rightNode = node;
else
this.rightNode.addNode(node);
//中序遍历;
public void infixList()
//按照左中右的顺序;
if(this.leftNode!=null)
this.leftNode.infixList();
System.out.println(this);
if(this.rightNode!=null)
this.rightNode.infixList();
测试一下刚开始;我手动创建的那棵二分搜索树
public static void main(String[] args)
//测试;
BSTree bsTree = new BSTree();
int[] array = 60,70,100,110,80,105,20,35,40,45,50,42,65,180,30;
for (int i : array)
bsTree.addNode(new TreeNode(i));
//前序遍历;
bsTree.infixList();
测试输出的中序遍历结果;实际就是
TreeNodeval=20
TreeNodeval=30
TreeNodeval=35
TreeNodeval=40
TreeNodeval=42
TreeNodeval=45
TreeNodeval=50
TreeNodeval=60
TreeNodeval=65
TreeNodeval=70
TreeNodeval=80
TreeNodeval=100
TreeNodeval=105
TreeNodeval=110
TreeNodeval=180
若按照代码这样的添加逻辑,做出来的树是这个结构的;
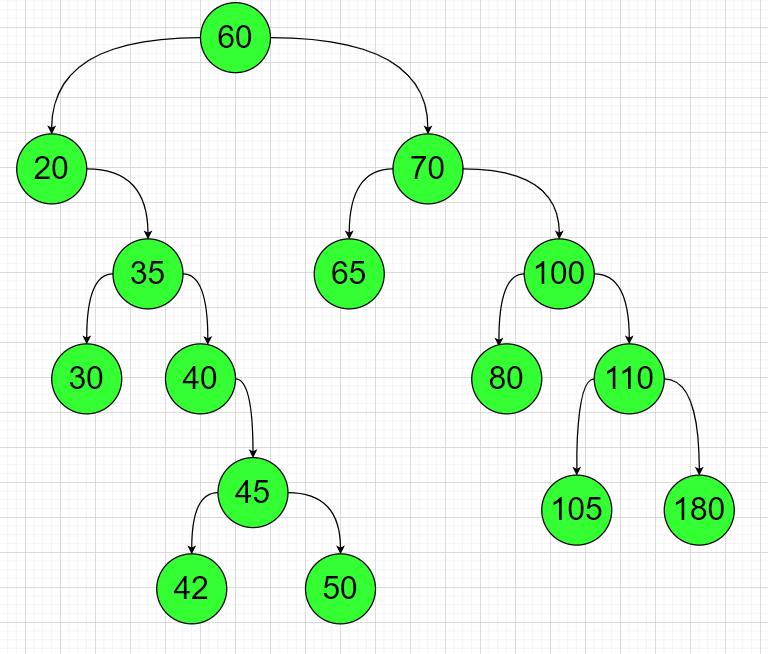
3.在二分搜索中删除节点
📢图解
在二分搜索树中要删除一个节点,需考虑到三种情况;
(1)删除的节点是一个叶子节点;
(2)删除的节点下挂接有一个子节点;
(3)删除的节点下挂接有两个子节点;
🚀(1)首先看这个删除结点是一个叶子节点的情况:
先找到这个需要删除的叶子节点;
然后找到这个即将删除结点的父节点;
然后还要确认这个要删除的节点是它父节点的左子节点还是右子节点;
然后再删除这个叶子节点;

比如这里被删除的节点是左子节点;
那么直接用节点30.LeftNode = null
🚀(2)删除的节点下有一个子节点的情况;
这个又会分为四种情况
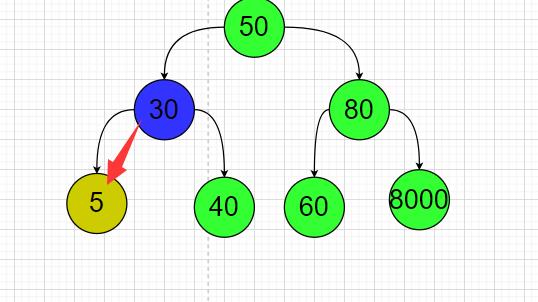
🛴先看第一种;被删除的节点是它父节点的左子节点;这个被删除的节点还有一个左子节点;
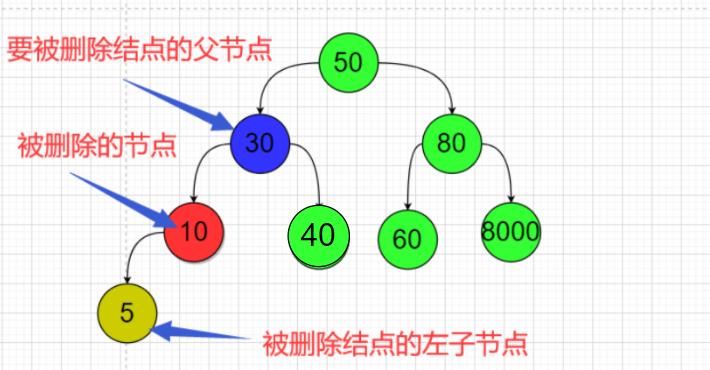
比如我这个案例中的删除节点10的时候;
让节点30.LeftNode == 节点10.LeftNode;
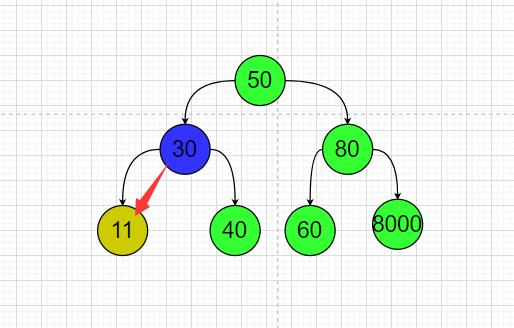
🛴第二种情况;被删除的节点是它父节点的左子节点;这时被删除节点还具有一个右子节点
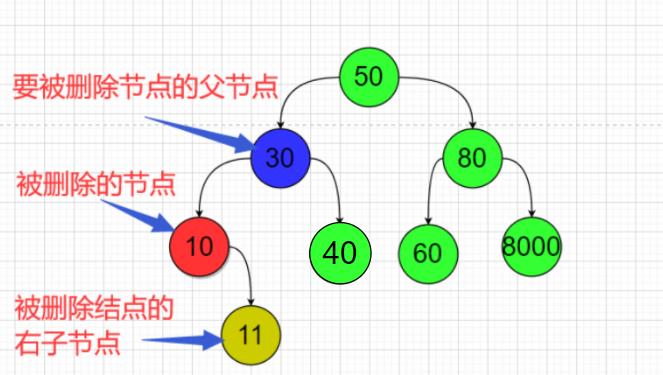
那么我这个案例的删除节点10的时候;
节点30.LeftNode == 节点10.RightNode;
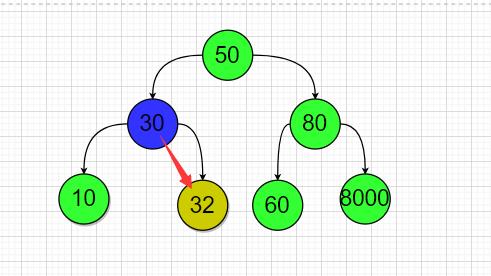
第三种情况;被删除节点是它父节点的右子节点;这个被删除节点还具有一个左子节点;
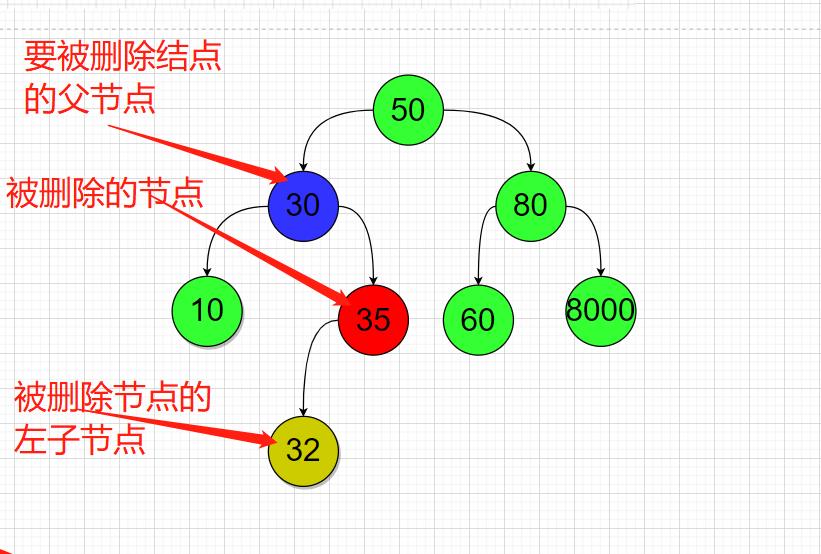
那么在这个案例下,我删除节点35时使用;
节点30.RightNode == 节点35.LeftNode;
第四种情况;这个被删除的节点是它父节点的右子节点;这个被删除节点还具有一个右子节点;
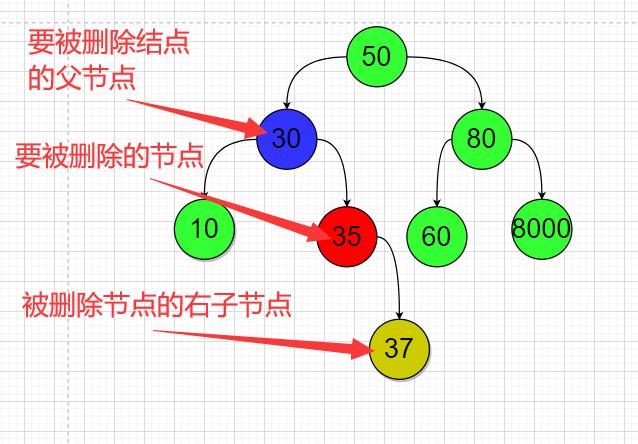
在这个案例中删除节点35;
节点30.RightNode == 节点35.RightNode;
🚀(3) 删除的节点下有两个子节点的情况
这里还是一样的,先找被删除节点的父节点;
然后可以分为两种情况去找
(1)找这个要被删除结点的右子树下的最小节点;然后替换掉这个要被删除的节点
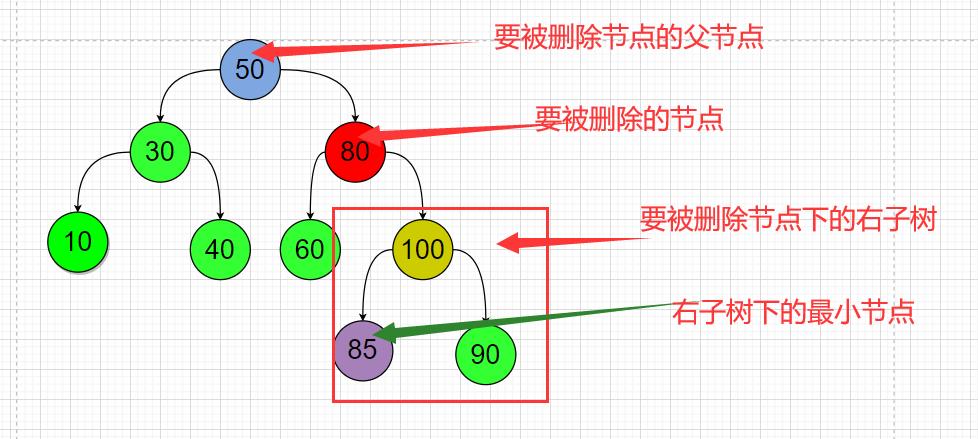
例如我这个案例删除节点80就是;
先把节点85临时存储起来;然后把这个节点85删除;
然后让节点85替换掉节点80的位置;实际上就是把节点80的左右子节点交给节点85;
(2)也可以考虑去找要被删除节点的左子树下的最大节点;然后替换掉这个要被删除的节点;
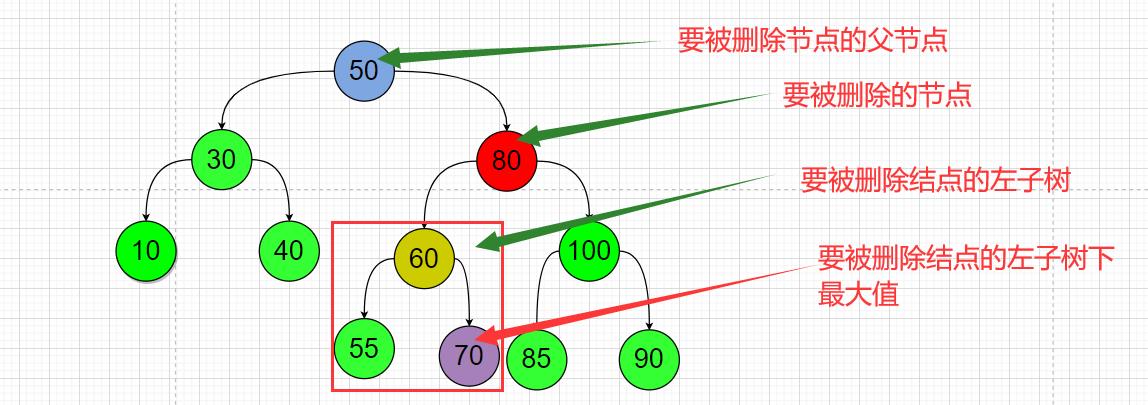
例如案例中;删除结点80;
首先把左子树下的最大节点70临时存储起来;
然后删除这个结点70;让节点70替换节点80
二分搜索树中删除结点的具体实现
/**
* @author by CSDN@小智RE0
* @date 2021-11-19 13:53
*/
//二分搜索树;
class BSTree
//根节点;
private TreeNode root;
//在二分搜索树添加节点;
public void addNode(TreeNode node)
//若根结点为空,则让新添加的第一个节点暂时作为根结点;
if (root == null) root = node;
else
root.addNode(node);
//中序遍历二分搜索树;
public void infixList()
if (root == null)
throw new RuntimeException("the tree is empty");
root.infixList();
/**
* 根据给定的值找到要删除的节点;(在二分树下定义)
*
* @param val 给定的数值
* @return 查找到要删除的节点;
*/
public TreeNode getTreeNode(int val)
if (root == null)
return null;
else
return root.getTreeNode(val);
/**
* 需要找到被删除节点的父亲节点;(在二分树下定义)
*
* @param val 要被删除的节点;
* @return 要被删除节点的父亲节点;
*/
public TreeNode getParentByDelete(int val)
if (root == null)
return null;
else
return root.getParentByDelete(val);
/**
* 删除结点;
*
* @param val 指定删除结点的值;
*/
public void deleteNode(int val)
if (root == null) return;
//1.先找要被删除的节点;
TreeNode wantDeleteNode = getTreeNode(val);
if (wantDeleteNode == null)
//未找到节点;
throw new RuntimeException("The node to be deleted was not found");
if ((root.leftNode == null && root.rightNode == null))
//若只有根节点,删除即可
root = null;
return;
//2.找删除结点的父亲节点;
TreeNode parentNode = getParentByDelete(val);
//一: 被删除的节点是叶子节点;
if (wantDeleteNode.leftNode == null && wantDeleteNode.rightNode == null)
//然后确认这个删除结点是它父节点的左节点还是右结点;
if (parentNode.leftNode != null && parentNode.leftNode.val == val)
//直接将父节点的左节点位置为空;
parentNode.leftNode = null;
else if (parentNode.rightNode != null && parentNode.rightNode.val == val)
//将父节点的右节点位置为空;
parentNode.rightNode = null;
//二: 被删除的节点下有两个子节点;
else if (wantDeleteNode.leftNode != null && wantDeleteNode.rightNode != null)
//删除并且找到右子树下的最小节点;
int rightTreeMinNode = getAndDelRightTreeMinNode(wantDeleteNode);
//让这个右子树下的最小节点代替这个要被删除的节点值;
wantDeleteNode.val = rightTreeMinNode;
//三: 被删除的节点下有一个子节点;
else
//这个被删除节点下的子节点是左子节点;
if (wantDeleteNode.leftNode != null)
//首先要考虑到父节点是否还存在的问题;
if (parentNode != null)
//这个删除节点是父节点的左子节点;
if (parentNode.leftNode.val == val)
parentNode.leftNode = wantDeleteNode.leftNode;
//删除节点是父节点的右子节点;
else
parentNode.rightNode = wantDeleteNode.leftNode;
else
root = wantDeleteNode.leftNode;
//这个被删除节点下的子节点是右子节点;
else
//首先要考虑到父节点是否还存在的问题;
if (parentNode != null)
//这个删除节点是父节点的左子节点;
if (parentNode.leftNode.val == val)
parentNode.leftNode = wantDeleteNode.rightNode;
//删除节点是父节点的右子节点;
else
parentNode.rightNode = wantDeleteNode.rightNode;
else
root = wantDeleteNode.rightNode;
/**
* 找到且删除右子树下的最小节点'
*
* @param node 当前传入的节点
* @return 返回的该节点树下的最下节点;
*/
public int getAndDelRightTreeMinNode(TreeNode node)
//实际是用一个临时节点去操作;
TreeNode tempNode = node;
while (tempNode.leftNode != null)
tempNode = tempNode.leftNode;
//删掉这个结点;
deleteNode(tempNode.val);
//返回节点;
return tempNode.val;
//节点
class TreeNode
//左节点,右节点;节点值;
TreeNode leftNode;
TreeNode rightNode;
int val;
//初始化节点;
public TreeNode(int val)
this.val = val;
@Override
public String toString()
return "TreeNode" + "val=" + val + '';
//添加节点的底层方法;
public void addNode(TreeNode node)
//先判断当前的节点是否为空;
if (node == null) return;
if (node.val <= this.val)
//考虑挂到左子节点;若左节点已经有了,则向左继续递归;
if (this.leftNode == null)
this.leftNode = node;
else
this.leftNode.addNode(node);
else
//右子节点;若有节点已经存在,则向右继续递归;
if (this.rightNode == null)
this.rightNode = node;
else
this.rightNode.addNode(node);
//中序遍历;
public void infixList()
//按照左中右的顺序;
if (this.leftNode != null)
this.leftNode.infixList();
System.out.println(this);
if (this.rightNode != null)
this.rightNode.infixList();
/**
* 根据给定的值找到要删除的节点;(在节点中实现)
*
* @param val 给定的数值
* @return 查找到要删除的节点;
*/
public TreeNode getTreeNode(int val)
if (val == this.val)
return this;
else if (val < this.val)
//在左子节点找;
if (this.leftNode != null)
return this.leftNode.getTreeNode(val);
else
//若左子节点为空,则说明找不到;
return null;
else
//在右子节点找;
if (this.rightNode != null)
return this.rightNode.getTreeNode(val);
else
//若右子节点为空,则说明找不到;
return null;
/**
* 需要找到被删除节点的父亲节点;(在节点下实现)
*
* @param val 要被删除的节点;
* @return 要被删除节点的父亲节点;
*/
public TreeNode getParentByDelete(int val)
//这里要保证不为空;即找到了被删除节点的父节点;
if ((this.leftNode != null && this.leftNode.val == val) ||
(this.rightNode != null && this.rightNode.val == val))
return this;
//找左子树;
else if (val <= this.val && this.leftNode != null)
return this.leftNode.getParentByDelete(val);
else if (val > this.val && this.rightNode != null)
return this.rightNode.getParentByDelete(val);
else
//没找到要删除节点的父节点; 比如根结点;
return null;
测试使用;例如,我删除叶子节点50
 --- [二分搜索树(BinarySearchtTree)]的主要内容,如果未能解决你的问题,请参考以下文章</p>
</article> </div> </div> </div> </section>
</div>
</div>
<script type=)