归并排序详解

Posted 2020-09-20

说一说归并排序

归并排序：归并排序（英语：Merge sort，或mergesort），是创建在归并操作上的一种有效的排序算法，效率为O(n log n)。1945年由约翰·冯·诺伊曼首次提出。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用，且各层分治递归可以同时进行。

 

归并排序的核心思想是将两个有序的数列合并成一个大的有序的序列。通过递归，层层合并，即为归并。

 

 

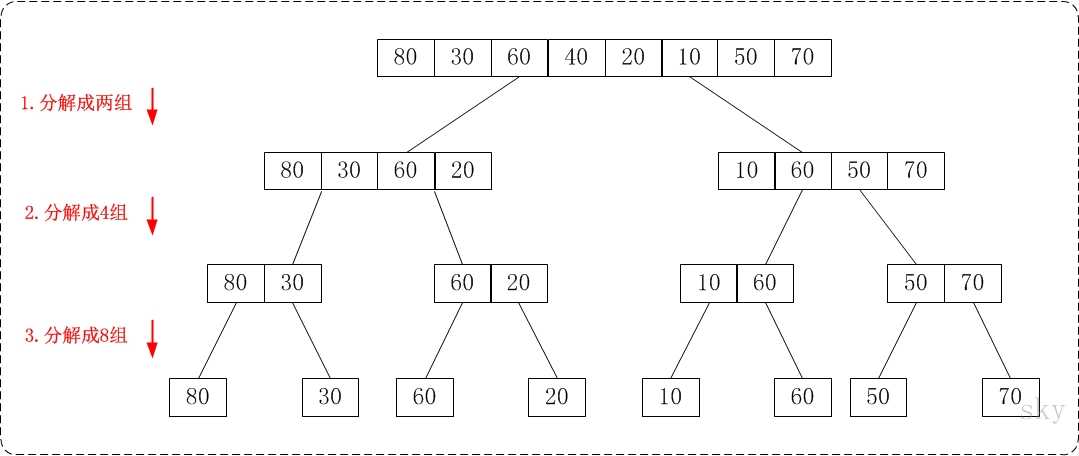
如图，从下到上，每一步都需要将两个已经有序的子数组合并成一个大的有序数组，如下是实现合并的具体代码，请读者细细体会

 1 void merge(int arr[],int l,int mid,int r)
 2 {
 3     int aux[r-l+1];//开辟一个新的数组，将原数组映射进去 
 4     for(int m=l;m<=r;m++)
 5     {
 6         aux[m-l]=arr[m];
 7     }
 8     
 9     int i=l,j=mid+1;//i和j分别指向两个子数组开头部分
10     
11     for(int k=l;k<=r;k++)
12     {
13         if(i>mid)
14         {
15             arr[k]=aux[j-l];
16             j++;
17         }
18         else if(j>r)
19         {
20             arr[k]=aux[i-l];
21             i++;
22         }
23                 else if(aux[i-l]<aux[j-l])
24                 {
25                     arr[k]=aux[i-l];
26                     i++;    
27                 }
28                 else
29                 {
30                     arr[k]=aux[j-l];
31                     j++;
32                 }
33     } 
34 } 

上图代码已经完成了归并中的“并”这一部分，归并归并，有并必有归，如下实现“归”的部分

1 void merge_sort(int arr[],int l,int r)
2 {
3     if(l >=r)
4         return ;
5     int mid=(l+r)/2; 
6     merge_sort(arr,l,mid);
7     merge_sort(arr,mid+1,r);
8     merge(arr,l,mid,r);
9 }

由于上图中的l，r不方便使用者调用，于是我们创建一个方便自己调用的my_merge_sort函数

1 void my_merge_sort(int arr[],int n)
2 {
3     merge_sort(arr,0,n-1);    
4 } 

以上我们便实现了归并排序中的归和并，归并排序是利用二分法实现的排序算法，时间复杂度为nlogn，是一种比较快速的排序算法。如下是笔者自己写的归并排序的全部代码，

 

 1 #include <iostream>
 2 using namespace std;
 3 
 4 
 5 void merge(int arr[],int l,int mid,int r)
 6 {
 7     int aux[r-l+1];//开辟一个新的数组，将原数组映射进去 
 8     for(int m=l;m<=r;m++)
 9     {
10         aux[m-l]=arr[m];
11     }
12     
13     int i=l,j=mid+1;//i和j分别指向两个子数组开头部分
14     
15     for(int k=l;k<=r;k++)
16     {
17         if(i>mid)
18         {
19             arr[k]=aux[j-l];
20             j++;
21         }
22         else if(j>r)
23         {
24             arr[k]=aux[i-l];
25             i++;
26         }
27                 else if(aux[i-l]<aux[j-l])
28                 {
29                     arr[k]=aux[i-l];
30                     i++;    
31                 }
32                 else
33                 {
34                     arr[k]=aux[j-l];
35                     j++;
36                 }
37     } 
38 } 
39 //递归的使用归并排序，对arr[l....r]排序 
40 void merge_sort(int arr[],int l,int r)
41 {
42     if(l >=r)
43         return ;
44     int mid=(l+r)/2; 
45     merge_sort(arr,l,mid);
46     merge_sort(arr,mid+1,r);
47     merge(arr,l,mid,r);
48 }
49 
50 void my_merge_sort(int arr[],int n)
51 {
52     merge_sort(arr,0,n-1);    
53 } 
54 
55 int main()
56 {
57     int a[6];
58     for(int i=0;i<6;i++)
59     {
60         cin>>a[i];
61     }
62     my_merge_sort(a,6);
63     for(int i=0;i<6;i++)
64     {
65         cout<<a[i]<<" ";
66     }
67     return 0;
68 } 

当然，上面实现的归并排序算法有它的不足之处，还能进一步优化，进一步加强他的性能，我们下次再聊。