第6章 约束满足问题CSP

Posted 2020-11-25 gru-blog

第六章 约束满足问题CSP

一、问题定义

问题定义

状态空间，状态被定义为在值域Di中的变量Xi；

当前状态；

转移模型；

目标测试，每个变量都有自己的赋值同时满足约束条件；

评估函数。

三个成分

X是变量集合
[ {X_1,...,X_n} ]
D是值域集合
[ {D_1,...,D_n} ]
,每个变量都有自己的值域。

C是描述变量取值的约束集合

特点

CSP的解是相容的、完整的赋值。

相容：不违反任何约束条件的赋值称为相容的或合法的赋值。

完整赋值：每个变量都已赋值。

约束图

结点为变量，边表示两者间有约束关系。

形式化

离散变量

有限值域：n个变量，值域集合大小为d，e.g. 布尔变量
无限值域：整数，字符串等

连续变量
e.g.如哈勃望远镜的实验日程安排，每次观察的开始，结束时间
线性约束,二次规划求解

一元约束：只涉及一个变量，SA!=green

二元约束：涉及两个变量，SA!=WA

高阶约束：涉及3个或者3个以上变量

全局约束：变量个数任意的约束称为全局约束

举例

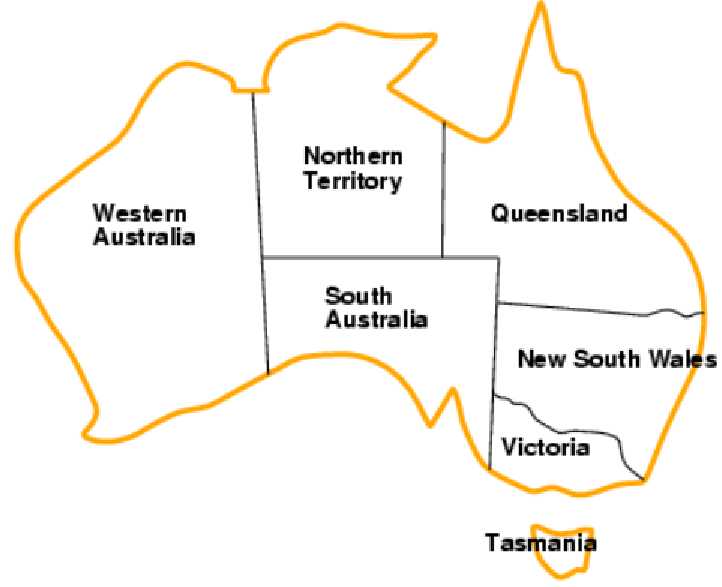
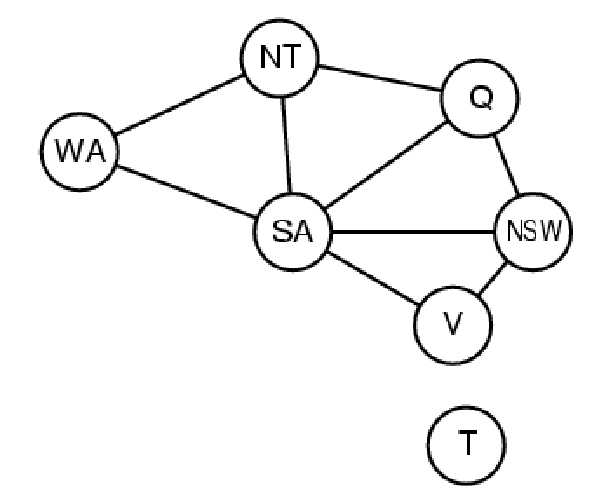
变量：WA, NT, Q, NSW, V, SA, T

值域：｛red,green,blue｝

约束条件：相邻的区域必须是不同的颜色

解之一：WA = red, NT = green,Q = red, NSW =green, V = red, SA = blue, T = green

二、推理——约束传播

思想

使用约束来减小一个变量的合法取值范围，从而影响到跟此变量有约束关系的另一变量的取值，如此进行。

相容

结点相容

单个变量值域中的所有取值满足一元约束

Eg., SA！=green 转化为SA的值域为{red,blue}

弧相容

某变量值域中的所有取值满足该变量的所有二元约束

e.g. Y=X^2, X,Y都是数字
弧相容<(X,Y),{(0,0),(1,1),(2,4),(3,9)}>

通用弧相容

Xi相对于某n元约束是相容的

e.g. 所有变量值域{0,1,2,3}，约束X<Y<Z,则如果X值域缩小为{0,1}称X是通用弧相容的。

弧相容算法

首先，工作集中包含CSP中所有的弧。AC-3从工作集中弹出弧(Xi,Xj)，首先使Xi相对于Xj弧相容。如果Di没有变化则继续处理下一条弧，否则每个指向Xi的弧（Xk，Xi）都必须重新插入工作集中准备检验。之所以这么做是因为Di的改变可能引起Dk的改变。如果Di成为空集，则无相容解。否则继续检查，直到工作集中没有弧。

function ac_3 (X, D, C){
    while (!worklist_empty()){
        (Xi,Xj)=remove_first(worklist)
        if revise(csp,Xi,Xj){
            if (sizeof(Di)==o){
                return false;
            }
            for each Xk in Xi.NEIGHBORD-{Xj} do{
                add(Xk,Xi)to worklist;
            }
        }
    }
    return true;
}
function revise(csp,xi,xj){
    revised=false;
    for each x in Di{
        if(no value y in Dj allows(x,y) to satisfy the constraint between Xi and Xj){
            delete x from Di;
            revised=true;
        }
    }
    return revised;
}  

时间复杂度
[ O（cd^3） ]
c个二元约束，变量值域最大为d个元素

路径相容

两个变量集合{Xi,Xj}对于第三个变量Xm是相容的，指{Xi,Xj}的每一个相容赋值{Xi=a,Xj=b}, Xm都有合适的取值同时使得{Xi,Xm},{Xm,Xj}是相容的。

e.g. 检查{WA,SA}对于NT在值域{red,blue}的条件下是否是相容的。

k相容

K相容：如果对于任何k-1个变量的赋值，第K个变量总能被赋予一个和前面k-1个变量相容的值。

如果一个图是k相容的，k-1相容的，…,直到1相容的，那么此CSP是强k相容的。

三、回溯搜索

通用搜索模式

状态是由赋值的变量决定的

通用的搜索模式
初始状态：设为空｛｝
步骤：给一个没有赋值的变量赋值，该赋值不与当前已赋值的变量相冲突
目标测试：如果所有赋值完成且满足终止状态，则搜索结束，否则搜索失败

CSP适用于通用的搜索模式，并采用深度搜索方法

回溯搜索

思想

对于CSP采用深度优先的单个变量赋值，当检测到不相容时，返回上一次赋值。

特点

变量的赋值顺序是可以交换的，在每一个结点只需要考虑一个变量的赋值，在算法之前需要固定变量的赋值顺序，叶子结点数减少到d^n。

提高算法效率的策略

选择变量赋值的顺序

选择值域中赋值的顺序

更早地检测不可避免的失败

最受约束变量

优先选择最少剩余值的变量进行赋值

约束最多变量

优先选择最能约束其他变量的变量进行赋值

最少约束值方法

选择使得剩余变量赋值空间更大的值

前向检验

思想

追踪未赋值变量的剩余合法赋值；当任何一个剩余变量没有合法赋值时搜索终止。

特点

前向检测从赋值变量向未赋值变量传播信息，但不能对失败提供早期检测。

改进MAC(维护弧相容)

当xi赋值后，从与xi邻接的弧中所有未赋值变量xj开始进行约束传播，一旦某变量的值域为空则回溯

例

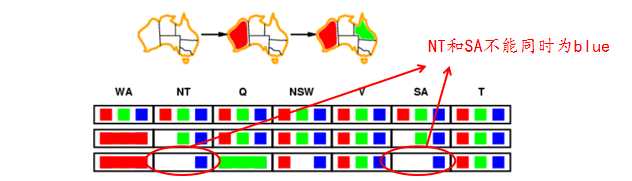
智能回溯

Solution：建立冲突集，回溯到冲突集中时间最近的赋值，SA的冲突集为{Q,NSW,V}，所以回溯到V

四、问题结构

独立的子问题

不相连的结构

e.g. Tasmania 与其他地区不相连

独立性子问题通过寻找连通子图来确定

拓扑排序

适用

求解树结构的CSP

思想

任意选择一个变量为树的根，选择变量顺序使每个变量在树中出现在父结点之后。

特点

n个结点n-1条弧，O(n)步将此图改造成直接弧相容,每一步比较两个变量的d个可能取值，所以总时间为O(nd^2)。

约束图到树

基于删除结点的方法

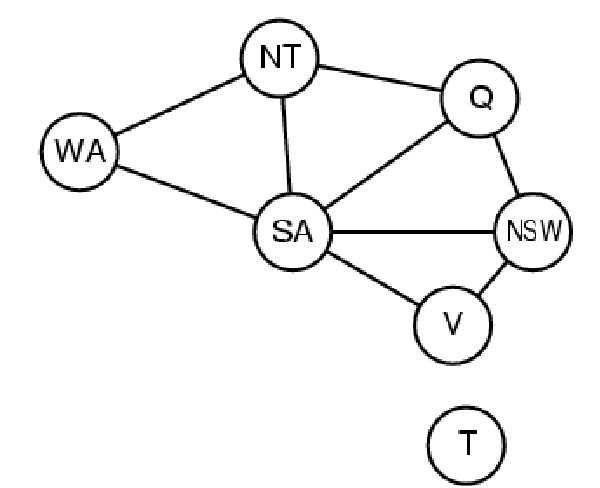
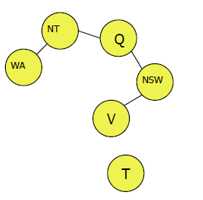
从CSP的变量中选择子集S（SA）,使得约束图在删除S后成为一棵树，S称为环割集

对于满足S所有约束的每个可能赋值

1. 求CSP剩余变量的值域，然后从中中删除与S的赋值不相容的值
2. 如果去掉S后的剩余CSP有解，把解和S的赋值一起返回

基于合并结点的方法

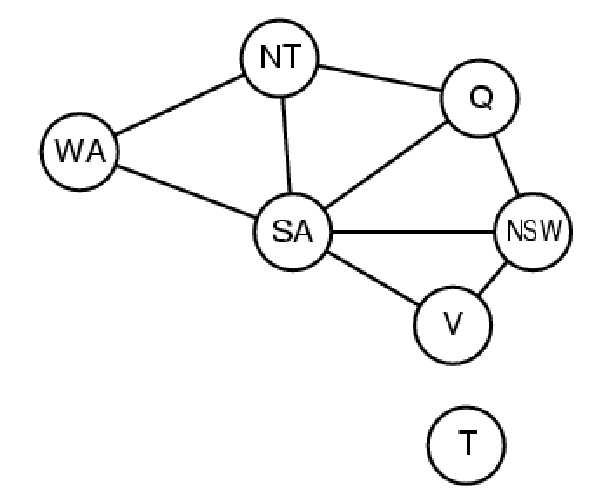
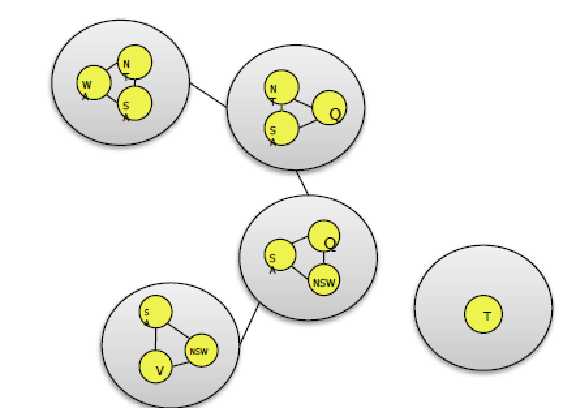
把约束图分解成相关联的子问题

对每个子问题单独求解，再把结果合并起来

树分解的三个条件

每个变量至少出现在一个子问题中

每个约束至少出现在一个子问题中

如果一个变量出现在两个子问题中，那么它必须出现在连接在这两个子问题的路径上的所有子问题中（？）