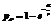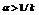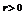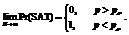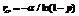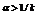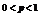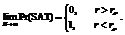两种改进的模拟退火算法求解大值域约束满足问题1.0

Posted 2020-08-16

0引言

约束满足问题（Constraint Satisfaction Problem，CSP）是人工智能研究领域中一个非常重要的分支，现已成为理论计算机科学、数学和统计物理学等交叉学科研究中的热点问题。人工智能、计算机科学和自动控制等领域中的许多问题都可以归结为约束满足问题。同时，约束满足问题在实际问题如模式识别、决策支持、物流调度及资源分配等领域也有着非常广泛的应用。

CSP由一个变量集合和一个约束集合组成。每个变量都有一个非空的可能值域，每个约束描述了一个变量子集与子集内各变量的相容赋值，所有约束的逻辑与构成了问题的一个实例。求解CSP，就是找到实例的解也就是找到满足所有约束的完全赋值（即对每个变量都进行赋值），或者在无解时使得可满足的约束数目最大化。拉丁方问题，N皇后问题，图着色问题，最小顶点覆盖，哈密顿回路问题以及合取范式的可满足性（Satisfiability，SAT）问题等都是约束满足问题。一般情况下，大多数的随机CSP都是NP-完全问题。近年来，大量的理论分析和算法实验表明：对于许多NP-完全问题，我们可以定义一个序参数（如约束密度，约束紧度等）按照随机实例的可满足性将其划分为亚约束区域和过约束区域。在亚约束区域，几乎所有的随机实例都是可满足的；而在过约束区域，几乎所有的随机实例都是不可满足的。一般认为，求解随机实例的难度在相变阈值点附近达到最高，难解实例大都分布在可满足概率突然转变的相变区域内。自从Cheeseman等人于1991年发现相变现象与难解性的联系以来，人们在CSP模型选择、算法设计和算法测试等方面进行了大量而深入的研究。

早期的许多理论研究和数值实验都是围绕四个标准的CSP模型展开的，由它们生成的随机实例被广泛地应用在算法测试中。但在1997年，D.Achlioptas等人指出这四种模型存在平凡的渐近无解性。为了克服这一缺点，人们提出了一些改进的CSP模型。如Y.Gao和J.Culberson等人在约束关系中加入特殊的结构，使生成的实例具有弧相容、路径相容、强3-相容或者弱4-相容的性质。虽然这些改进的模型能产生非平凡的难解实例，但是实例已不再是以简单、自然的方式生成的。2000年，K.Xu等通过对变量值域（随问题规模增加呈多项式级增长）和约束紧度（或约束密度）的限制提出了标准B模型的修改模型即RB模型。该模型避免了B模型不能产生难解实例的缺点。K.Xu等利用二阶矩方法严格证明了RB模型不但存在可满足性相变现象，而且可以得到精确的可满足性相变点。此后，针对RB模型的一系列研究相继展开。2006年，K.Xu等又从理论上证明RB模型的随机实例在相变区域具有指数级的树归结复杂性，即这些实例几乎是极其难解的。同时，实验上也验证了在相变阈值附近，随机实例的求解难度随着问题规模增加而呈指数级增长，并在相变阈值处达到顶峰。因此基于RB模型生成的难解算例被广泛地应用于各种算法竞赛作为测试算法的基准（benchmark）。由RB模型生成的随机实例的求解难度，甚至在问题规模仅为10²量级时已极具挑战性。一方面，2011年，C.Zhao等引入统计物理中的有限尺度分析方法，给出了在有限尺度效应下，RB模型相变区域尺度窗口的上界。同时，受RB模型启发，J.Shen提出了一个值域固定的随机d-k-CSP模型，证明了在一定条件下该模型也存在精确的相变现象，并可以产生非平凡的具有小值域的随机实例。2015年，G.Zhou等弱化了k-CSP模型存在精确相变现象的条件。另一方面，2011年，C.Zhao等提出了由Belief Propagation引导的消息传递算法来求解由RB模型生成的变量具有大值域的随机实例。随后，C.Zhao等利用无序系统中的空腔方法，分别在文献中提出了一种基于变量熵的Belief Propagation算法，在文献[22]中提出了Reinforced Belief Propagation算法来求解RB模型的随机实例，并进一步指出了解空间的结构特征和算法求解复杂性之间的联系。

本文针对RB模型这一类具有较大值域的随机CSP，提出了两种改进的模拟退火算法（Simulated Annealing）即RSA和GSA。在RSA算法中，将温度控制引入到扰动策略中；在GSA算法中，初始解不再是随机生成的，而是利用改进的遗传算法（Genetic Algorithm）来得到模拟退火算法的初始解。将这两种算法用于求解RB模型的随机实例，数值结果表明：在约束紧度进入相变区域时，算法都能有效地找到实例的解。与随机游走算法对比，这两种算法都具有明显的优越性。在约束紧度临近相变点时，求解难度呈现指数级增加，这两种算法虽然不再能有效地找到实例的解，但是得到的最优解仅使得极少数的约束不能满足。因此，这两种改进的模拟退火算法对具有较大值域的随机CSP的求解起到了积极的促进作用。

1   RB模型

我们用三元组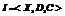表示由RB模型生成的随机实例，其中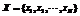是变量集合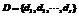；是变量的取值集合即值域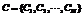；是约束集合。我们由以下两步来生成RB模型的随机实例。

Step1：随机可重复地挑选M个约束，每个约束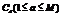限制了X的子集合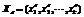的取值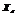，中的元素是从X中随机挑选的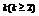个互异变量，这里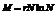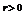，是常数；

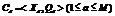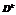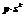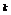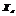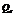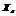Step2：对于每个约束，随机不重复地从中选取个-元赋值作为的不相容赋值集合，即若对的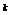-元赋值属于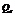，则约束是不可满足的，反之就是可满足的。这里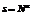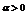（为常数）随着问题规模即变量数目N的增加呈多项式级增长，

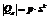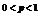，为常数。

控制参数r和p分别代表了约束密度和约束紧度，文献分别从理论和实验上证明RB模型存在精确的可满足性相变现象，同时在相变区域涌现出了大量难解实例。用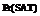表示由RB模型生成的随机实例可满足的概率，则有以下结论成立：

定理1设，若，且，则

定理2设，若，且，则

RB模型中，变量的值域随着N的增加呈多项式级增长，因此当N充分大时，变量的值域也会相应地变得较大。上述两个定理表明RB模型存在精确的可满足性相变现象，故RB模型是具有大值域并能产生非平凡随机CSP实例的模型。设计求解由RB模型生成的随机实例的算法，可以用来解决一类具有大值域的随机CSP。