图解AC自动机

Posted 2020-11-25 zxytxdy

图解AC自动机

前言：

• 我们引出这样一个问题：
  • 我想知道字符串(t)在字符串中(s)出现多少次/有没有出现？
  • 那我们可以使用kmp算法求出(t)的next数组，之后(O(n))匹配求解即可。
• 那如果把问题升级一下呢？
  • 想知道字符串(t_1,t_2,...,t_n)在字符串(s)中出现了多少次/有没有出现？
  • 这时候再用(kmp)算法，复杂度将达到(O(n^2))，非常慢了。
  • 这时候我们需要AC自动机。
• AC自动机用于求解多个模式串与一个文本串的匹配问题。
• AC自动机需要提前知道所有需要匹配的字符串。
• 可以想象成trie树上kmp。

开始图解：

假设说我们的模式串分别为：(abcd,abd,bcd,cd)。

第一步：创建trie树

• 没啥好说的，建立trie就行了呗。

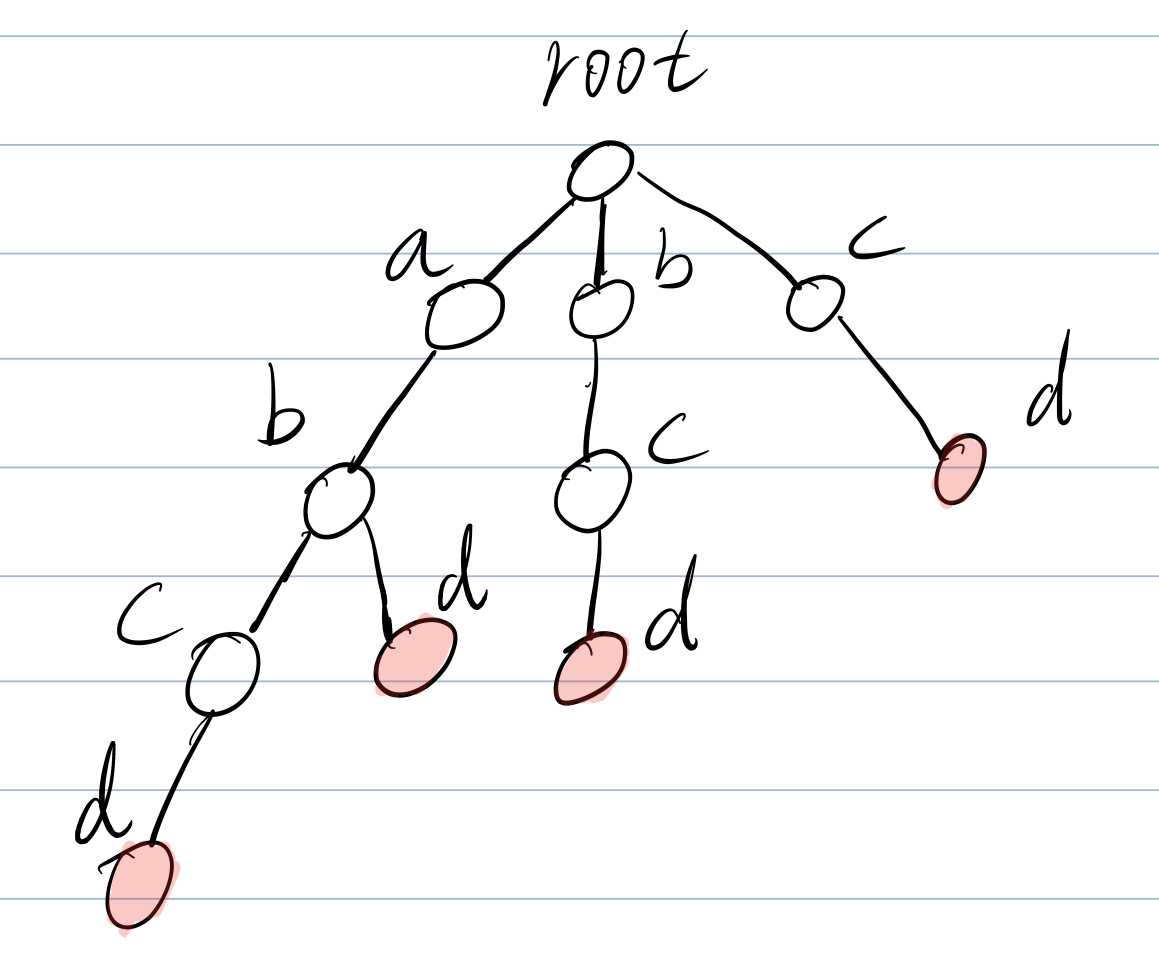
• 其中红色节点代表一个字符串的结尾。

第二步：构建失配指针（最重要的一步）

• 这一步的目的和kmp算法中求nex数组的目的是类似的。
• 对于kmp算法来说，是求next；对于AC自动机来说，是求fail指针。
• (fail(i):)以(i)节点为结尾的串的后缀与其他串有最大公共长度的前缀的结尾编号。
• 可能看到这里比较懵逼，没关系，模拟一下就好了。
• 首先看第一个字符串：(abcd)，不存在任何一个其他子串的前缀与(abcd)相匹配。
• 但是(bcd)与(abcd)的后缀(bcd)相匹配，这是匹配到的最长的情况，于是(abcd)上的(d)的(fail)指针指向(bcd)上的(d)。
• 这时候再去看看(fail)的定义，是不是觉得清晰了一些呢？

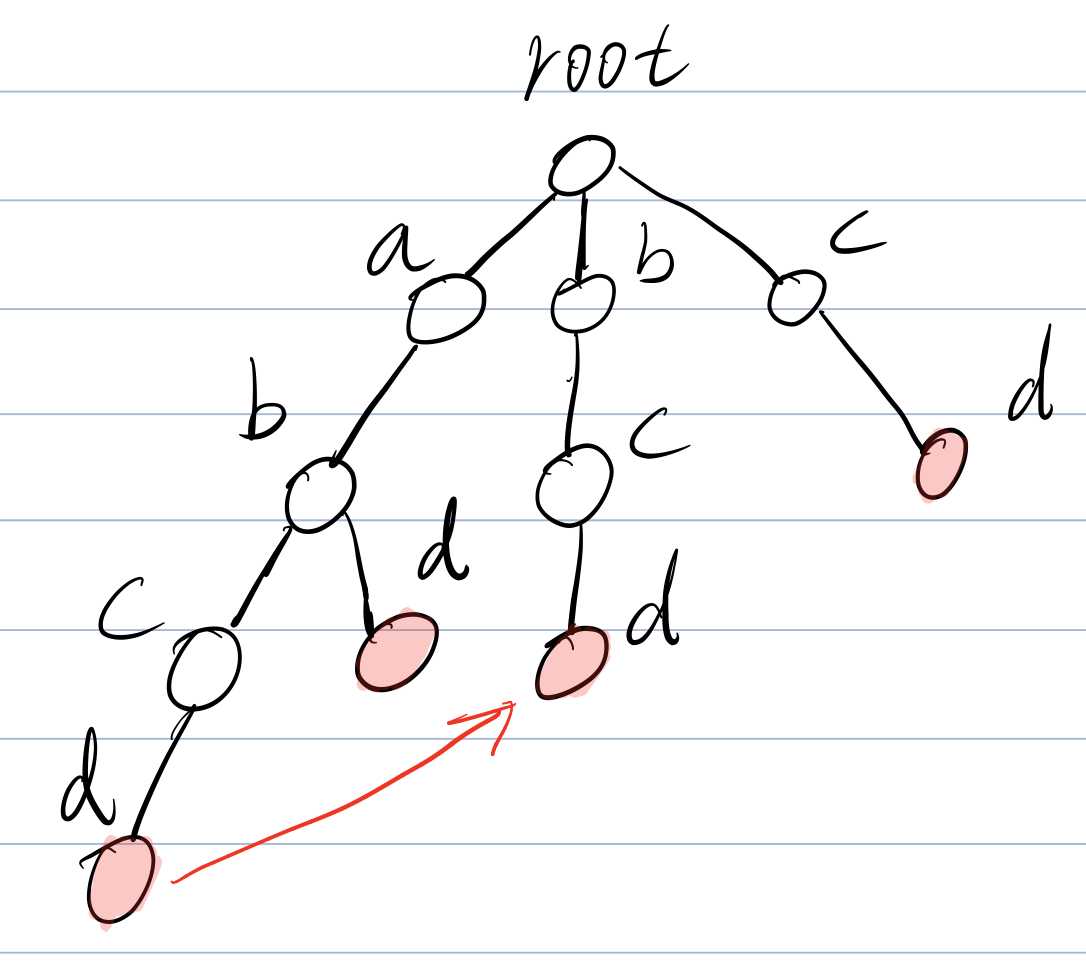
• 那么自然(bcd)上的(d)会指向(cd)上的(d)，(abcd)上的子串(abc)的(c)会指向(bcd)上的(c)。
• 同样应该也能理解(root)的所有直接子节点的(fail)指针指向(root)。
• 如果没有找到任何一个前缀与当前串的任何一个后缀相等，那么(fail)指针指向(root)节点。
• 这和kmp的nex数组第一位为0道理相同。（假设字符串数组以1开头）
• 我们画出完整的(fail)指针：

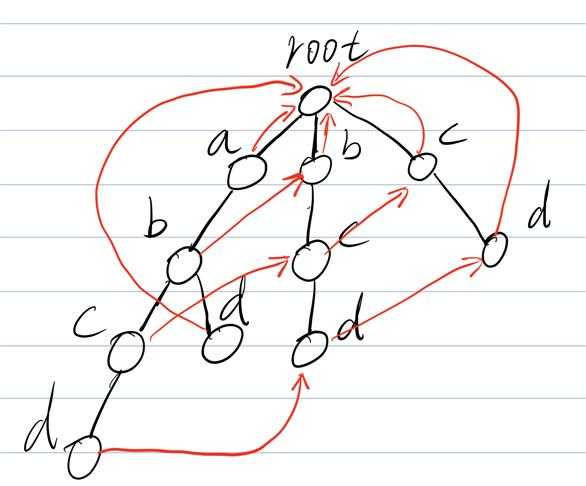
• 与kmp原理相同，fail指针跳到的地方的前面的子串就不用比较了。
• 接下来我们看看当前节点要是匹配不下去了怎么办？
• 比如说尝试匹配(abcde)，(abcd)都顺利的匹配了，这是(d)没有(e)这个子节点，那么就直接跳到(d)的(fail)指针(bcd)上面的(d)，他也没有子节点(e)，那就继续直到根节点，那就没有了。

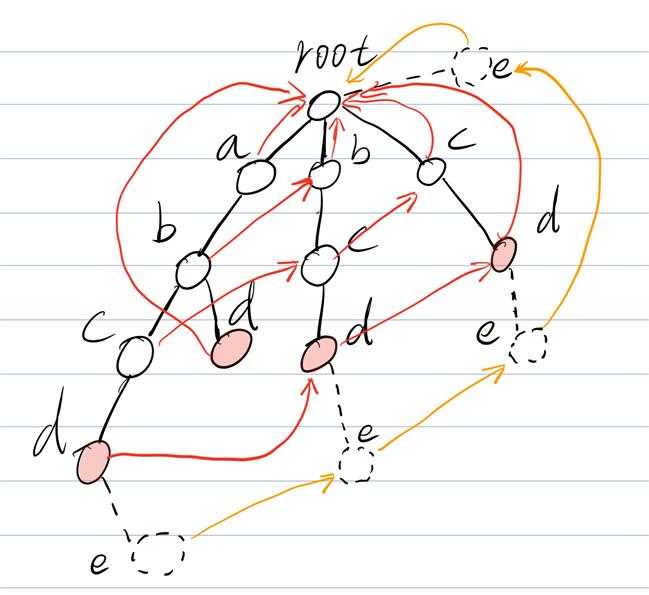
• (e)为虚线，实际上不存在。
• 而且应该也可以发现，构建(fail)指针是一个(bfs)的过程。
• 那匹配的过程其实就相当于是取文本串在(trie)树上一层一层的遍历比如说我的文本串是(abcd)，那么他就会沿着(trie)树到(trie)树上的(abcd)，然后根据失配指针跳到(bcd)的(d)，如果(bcd)的(d)是一个模式串的结尾（在这里显然是），那就统计上答案。

例题：

• 洛谷3808：AC自动机（简单版）：代码

• 洛谷3796：AC自动机（加强版）：代码