数据结构与算法简记--二叉树

Posted 2020-11-23 wod-y

二叉树（Binary Tree）

---

 

树

• 根节点、父节点、兄弟节点、叶子节点

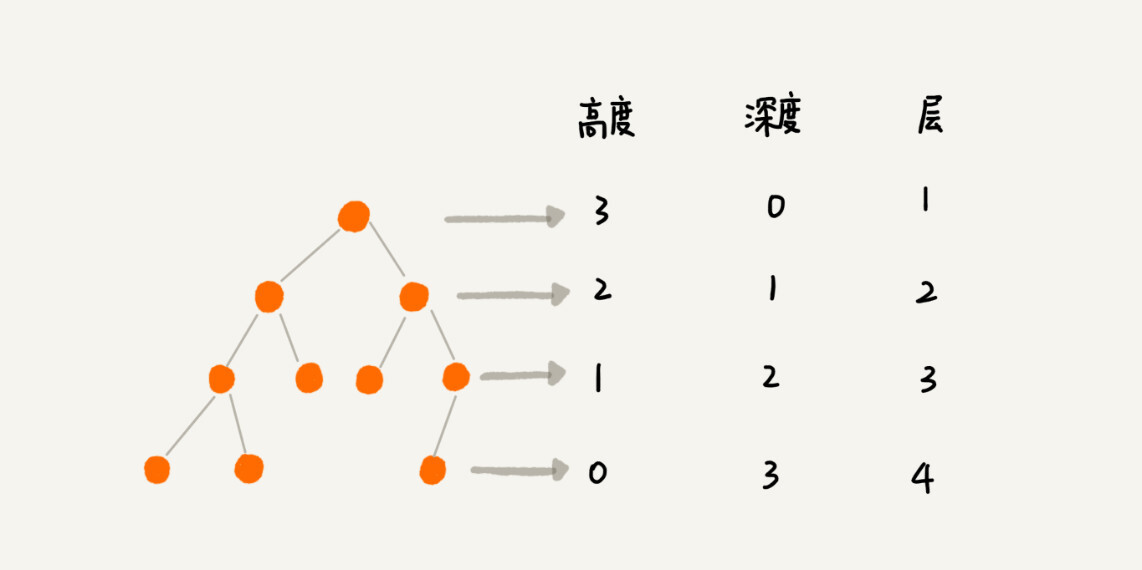
• 高度、深度、层的概念

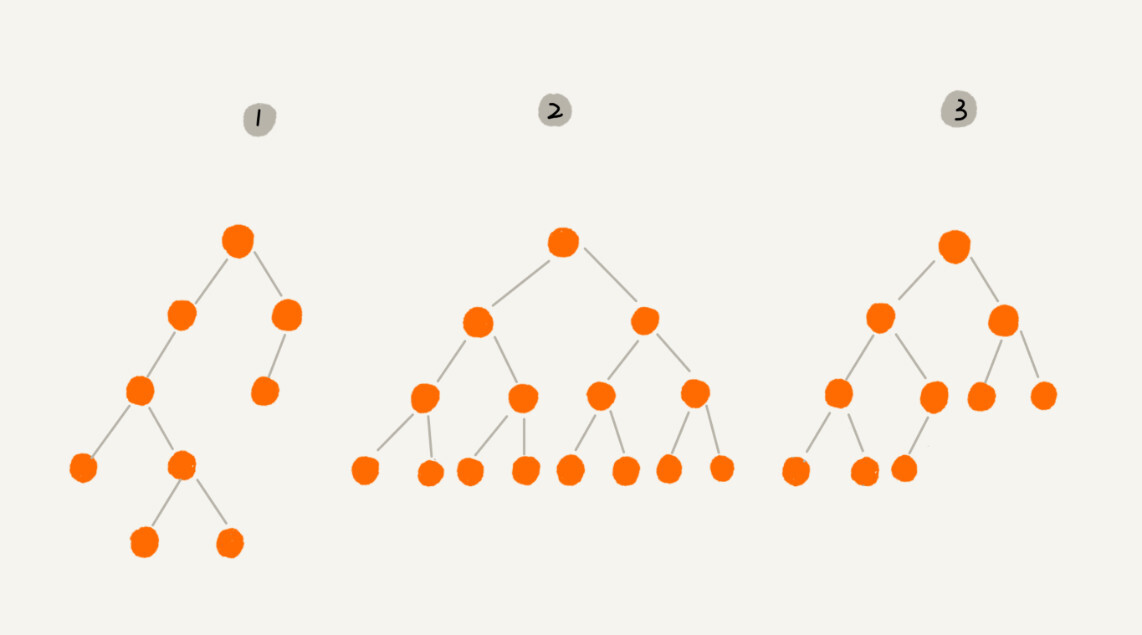
二叉树

顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子节点和右子节点，并不要求都要有二个节点，有的只有左节点，有的只有右节点

满二叉树

• 图中编号2的二叉树，叶子节点全都在最底层，除了叶子节点之外，每个节点都有左右两个子节点，这种二叉树就叫作满二叉树

完全二叉树

• 图中编号3的二叉树，叶子节点都在最底下两层，最后一层的叶子节点都靠左排列，并且除了最后一层，其他层的节点个数都要达到最大，这种二叉树叫作完全二叉树

如何表示（或者存储）一棵二叉树？

• 链式存储法
• 顺序存储法
  • 基于数组
  • 如果节点 X 存储在数组中下标为 i 的位置，
  • 下标为 2 * i 的位置存储的就是左子节点，
  • 下标为 2 * i + 1 的位置存储的就是右子节点。
  • 反过来，下标为 i/2 的位置存储就是它的父节点。通过这种方式，我们只要知道根节点存储的位置（一般情况下，为了方便计算子节点，根节点会存储在下标为 1 的位置），这样就可以通过下标计算，把整棵树都串起来。
  • 适用于完全二叉树，如果是非完全二叉树会浪费空间；
  • 堆就是完全二叉树，且常使用数组存储数据

二叉树的遍历

• 前序遍历--访问顺序：父节点--》左子节点--》右子节点
• 中序遍历--访问顺序：左子节点--》父节点--》右子节点
• 后序遍历--访问顺序：左子节点--》右子节点--》父节点

二叉查找树（Binary Search Tree）