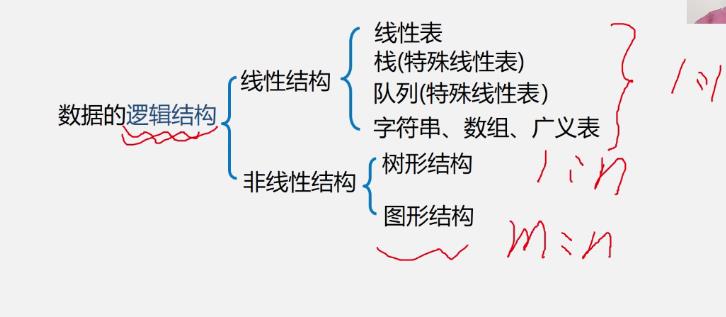
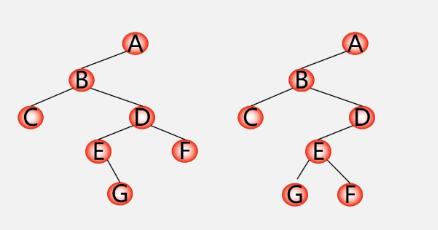
数据结构与算法学习笔记 树
Posted 临风而眠
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了数据结构与算法学习笔记 树相关的知识,希望对你有一定的参考价值。
数据结构与算法学习笔记(7) 树
前情回顾
一.树和二叉树的定义
1.树
树的定义

递归嵌套定义
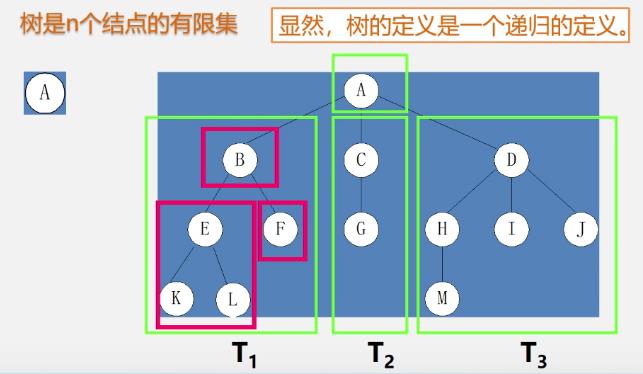
-
树的其他表示方式
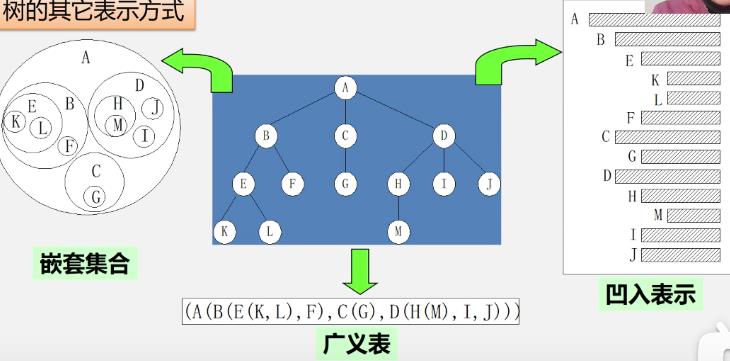
就有点像这个markdown语法:
- A
- B
- E
- K
- L
- F
- C
- G
- D
- H
- M
- I
- J
树的基本术语

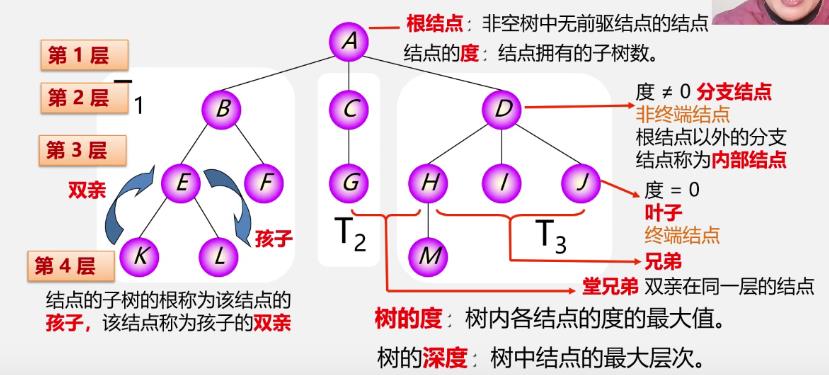
结点的度,也是分支个数,也是后继个数
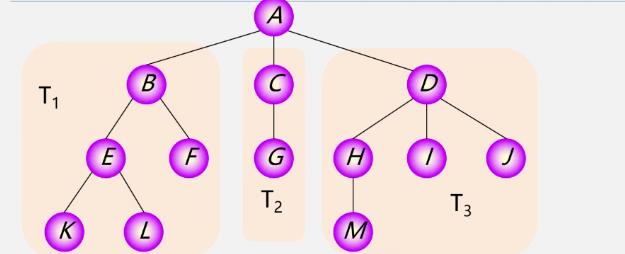
-
有序树:树中结点的各子树从左至右有次序(最左边为第一个孩子)
-
无序树:树中结点的各子树无次序
-
森林:是m(m≥0)棵互不相交的树的集合
树变森林:
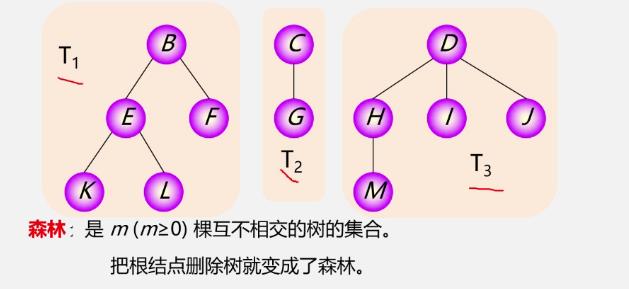
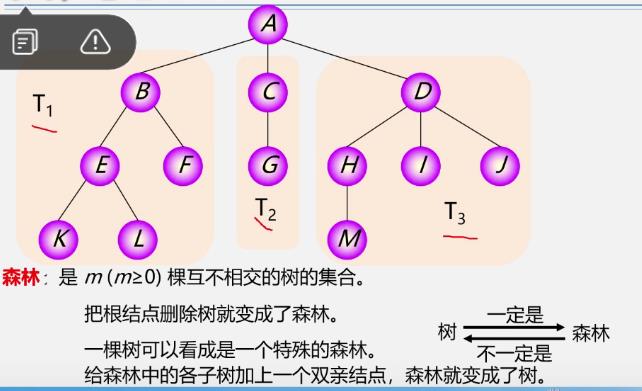
-
树结构与线性结构比较

2.二叉树

二叉树的定义

二叉树与树的差别
二叉树与树是两个概念,二叉树不是树的特殊情况

-
例
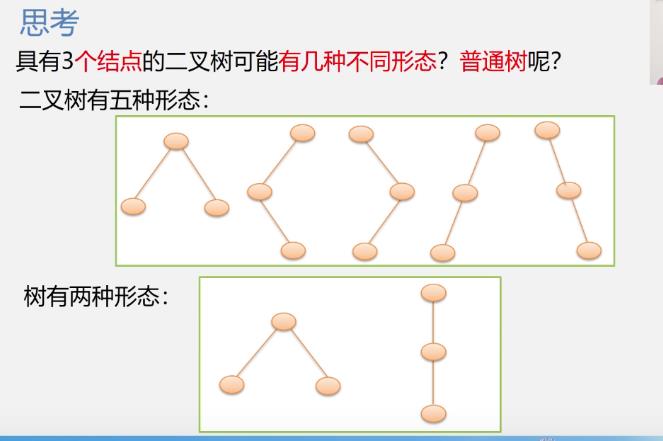
-
虽然是两个概念,但是有关树的基本术语对二叉树都适用
二叉树基本形态
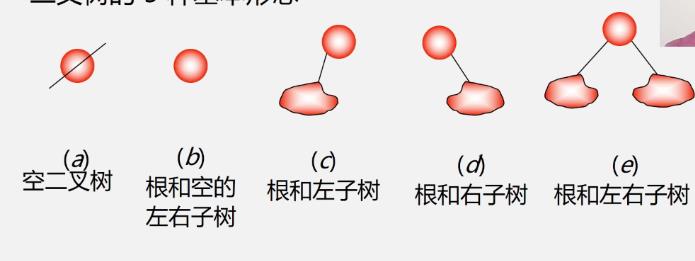
3.树和二叉树的抽象数据类型定义
树:
-
主要学习二叉树的抽象数据类型定义

-
基本操作很多,下为几个主要的:

-
二.二叉树的性质与存储结构
1.二叉树的性质
①二叉树性质1、2、3
-
每层结点个数
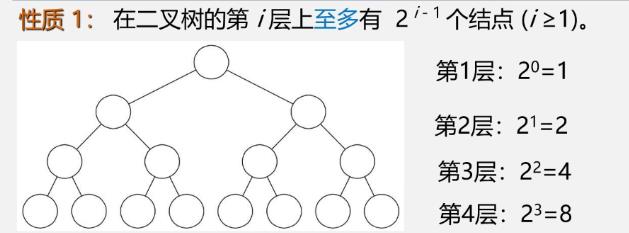
- 第i层上至少有1个结点
-
总共结点个数

-
叶子数与度为2的结点数的关系
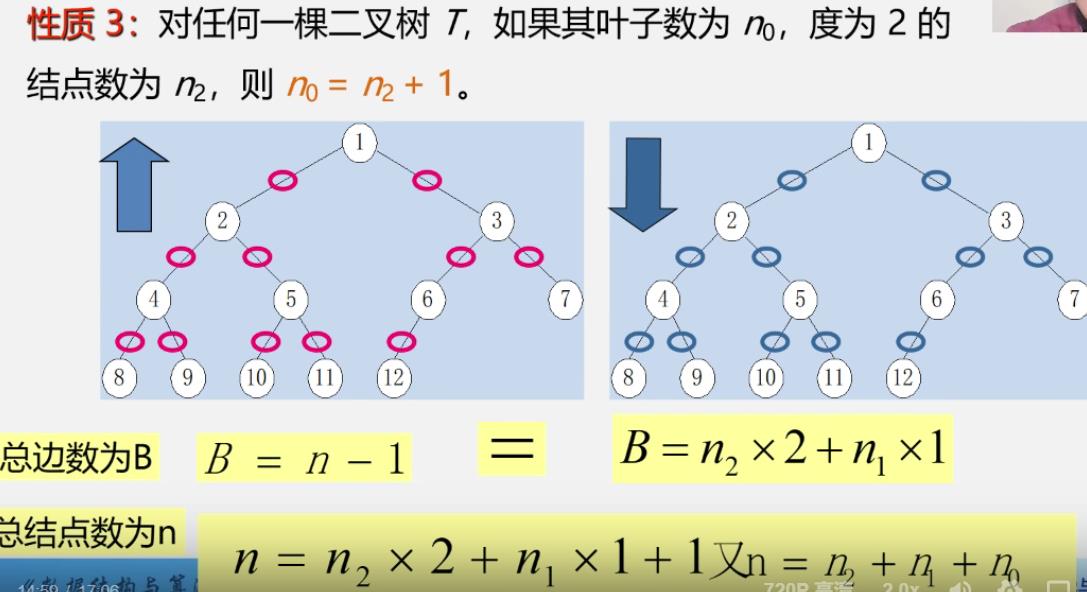
n表示结点总个数
n 1 n_1 n1表示度为1的结点
- 🤩从上往下然后从下往上的思想
②两种特殊形式的二叉树:满二叉树和完全二叉树
定义与特点
- 满二叉树


-
完全二叉树
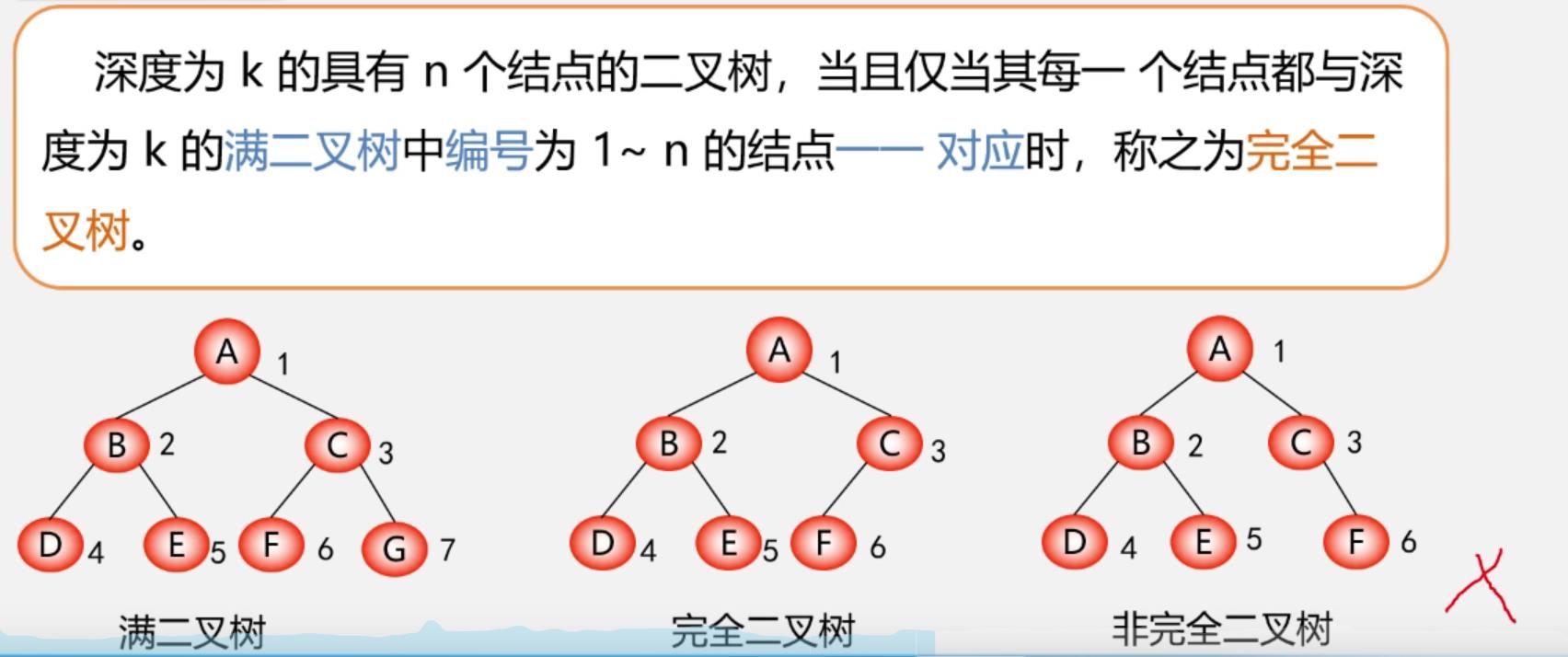
-
判断技巧
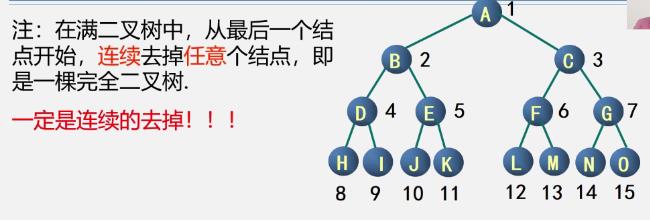
-
特点
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QTpIvBoR-1637761025234)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20210928093038.png)]
-
两者关系

③二叉树的性质4、5(完全二叉树的两个性质)
- 性质4:完全二叉树的深度


-
性质5:结点编号之间的关系
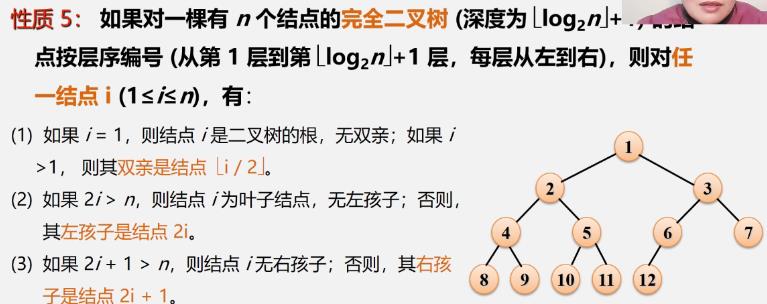
-
性质5表明了完全二叉树中双亲结点编号与孩子结点编号之间的关系
证明:数学归纳法
-
判断完全二叉树:借助队列
2.二叉树的存储结构
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LWSp7IJN-1637761025237)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211005081221.png)]
①顺序存储
-
实现:按满二叉树的结点层次编号,依次存放二叉树中的数据元素
-
如:
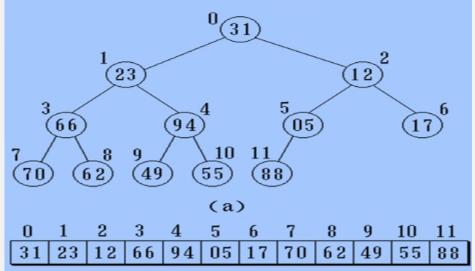
先从上到下,再从左到右
-
类型定义
#define MAXTSIZE 100 typedef TElemType SqBiTree[MAXTSIZE]; SqBiTree bt;上面SqBiTree是一个数据类型, 定义 的变量类型就是TElemType[MAXTSIZE]
即上面的bt就是一个TElemType类型的有MAXTSIZE个元素的数组
-
看个例子

-
二叉树顺序存储的特点
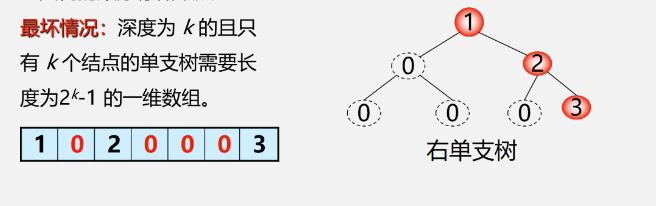

②链式存储
二叉链表
-
二叉树结点的特点
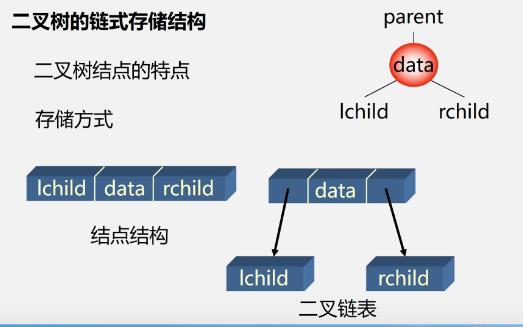
-
存储结构定义
typedef struct BiNode TElemType data; struct BiNode *lchild,*rchild; //左右孩子指针 BiNode,*BiTree;- 看个例子


-
空指针域的个数
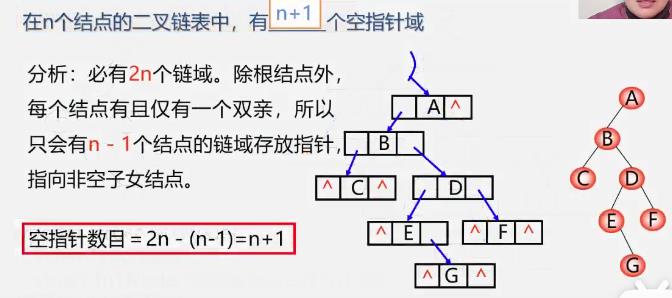
- 每个结点都有一个和其双亲的连线,除了根节点
- 所以只会有n-1个结点的链域存放指针,指向非空子女节点
- 每个结点都有一个和其双亲的连线,除了根节点
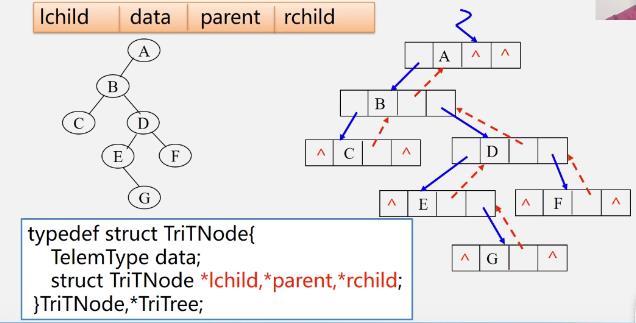
三叉链表
-
有时候需要找前驱
三.遍历二叉树和线索二叉树

1.遍历方法概述
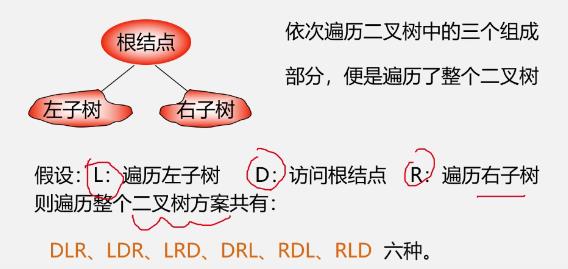
-
重点研究DLR、LDR、LRD三种



由二叉树的递归定义可知,遍历左子树和遍历右子树可如同遍历二叉树一样"递归"进行
先序遍历二叉树的操作定义
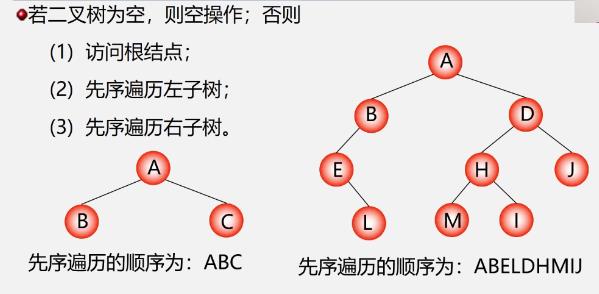
中序遍历二叉树的操作定义
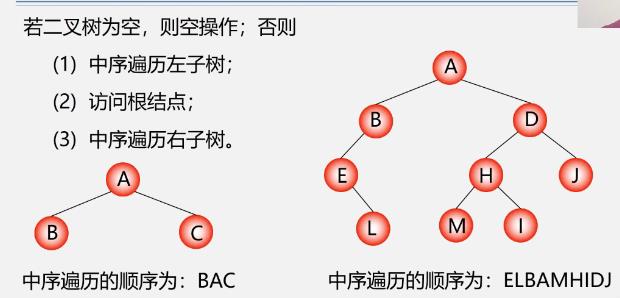
后序遍历二叉树的操作定义
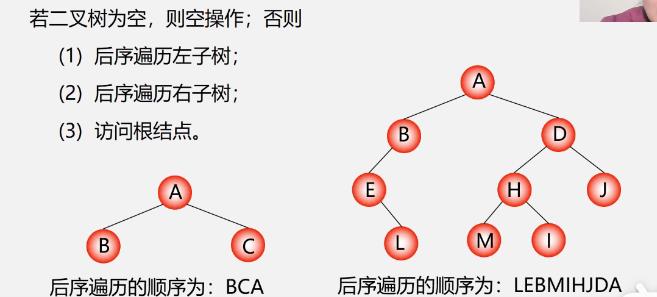
例
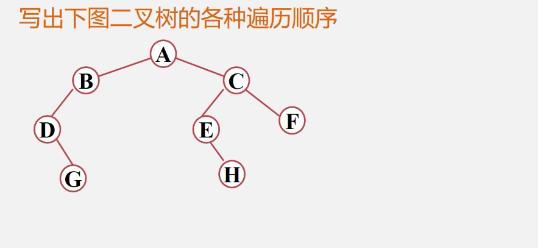
- 先序:ABDGCEHF
- 中序:DGBAEHCF
- 后序:GDBHEFCA
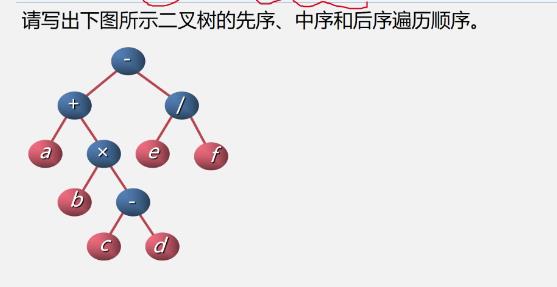
-
先序:-+a×b-cd/ef
-
中序:a+b×c-d-e/f
-
后序:abcd-×+ef/-

2.根据遍历序列确定二叉树
-
若二叉树中各结点的值均不同,则二叉树结点的先序序列、中序序列、后序序列都是唯一的
-
由二叉树的先序序列和中序序列,或由二叉树的后序序列和中序序列可以确定唯一 一颗二叉树
-
例
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hgeNdYCK-1637761025258)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211005094048.png)]
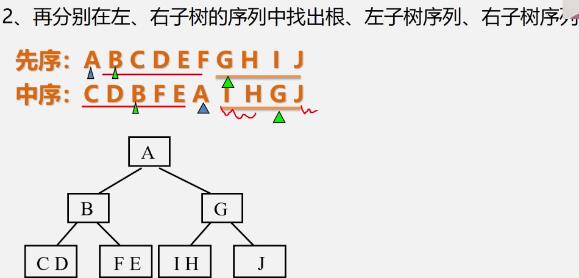
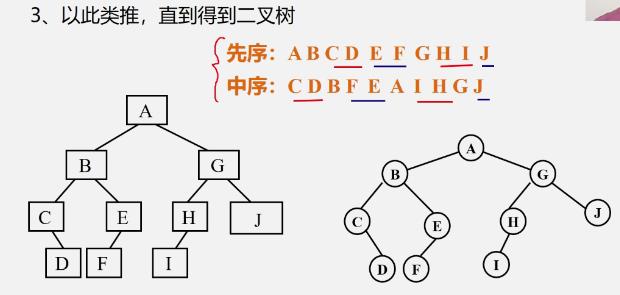
-
例
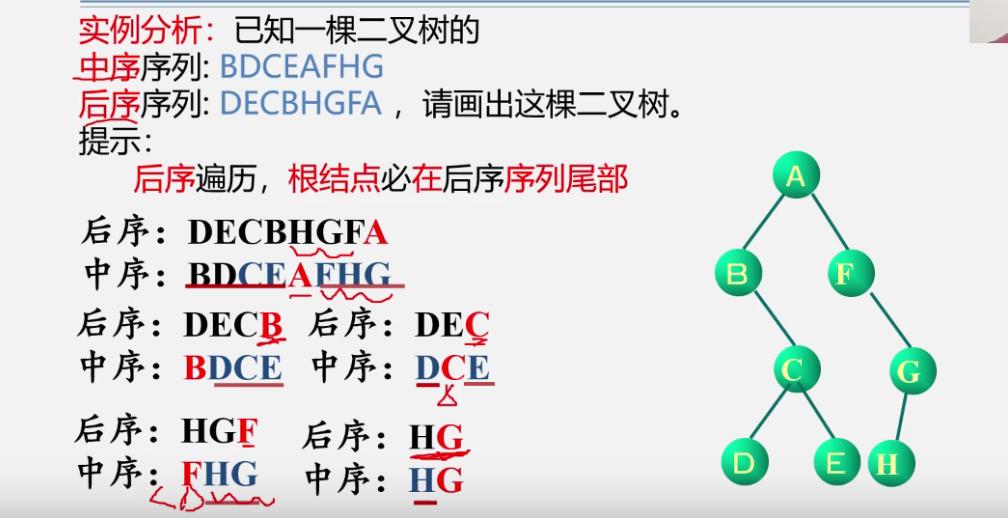
-
3.二叉树的遍历方法实现
先序遍历递归算法

Status PreOrderTraverse(BiTree T)
if(T==NULL) return OK; //空二叉树
else
visit(T); //访问根结点
PreOrderTraverse(T->lchild); //递归遍历左子树
PreOrderTraverse(T->rchild); //递归遍历右子树
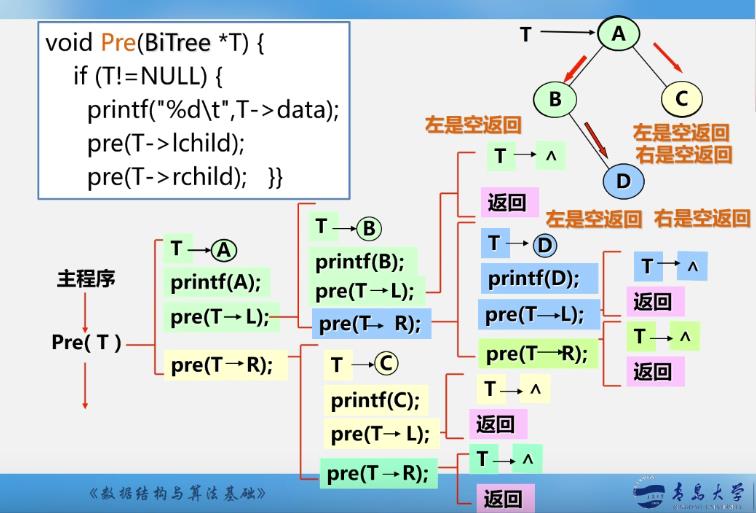
-
先序序列
ABDC
中序遍历递归算法
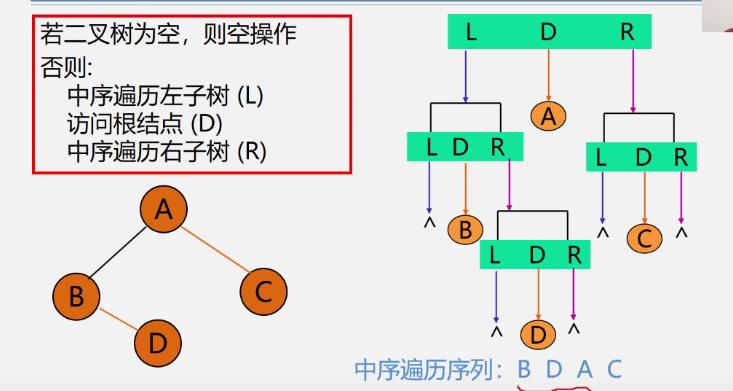
Status InOrderTraverse(BiTree T)
if(T==NULL) return OK; //空二叉树
else
InOrderTraverse(T->lchild); //递归遍历左子树
visit(T); //访问根结点
InOrderTraverse(T-rchild); //递归遍历右子树
后序遍历递归算法
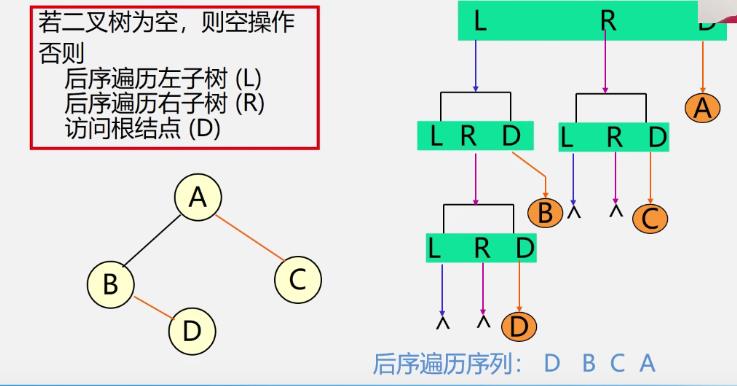
Status PostOrderTraverse(BiTree T)
if(T==NULL) return OK; //空二叉树
else
PostOrderTraverse(T->lchild); //递归遍历左子树
PostOrderTraverse(T-rchild); //递归遍历右子树
visit(T); //访问根结点
三种递归遍历算法的比较分析
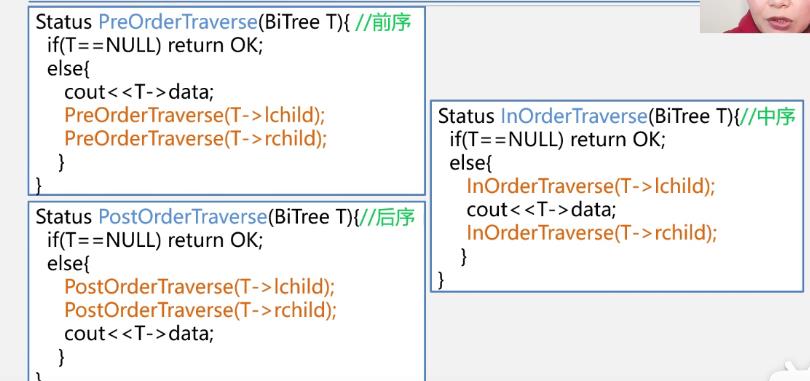
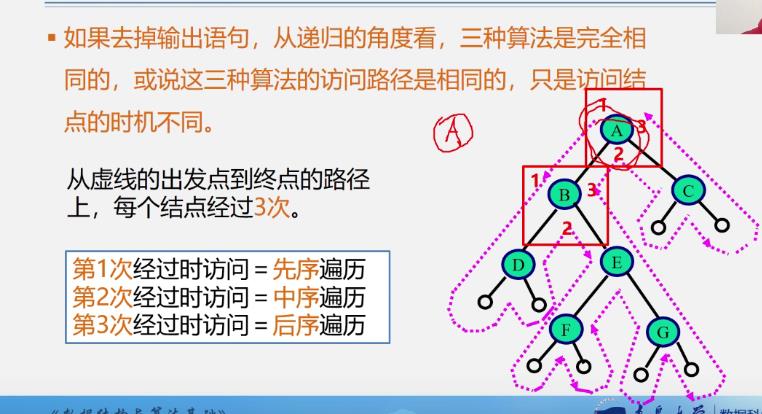

空间用的是栈
中序遍历非递归算法


Status InOrderTraverse(BiTree T)
BiTree p;
InitStack(S);
p=T; //指向根结点
while(p||!StackEmpty(S))
if(p)
Push(S,p);
p=p->child;
else
Pop(S,p);
printf("%c",q->data);
p=q->child;
return OK;
二叉树的层次遍历算法
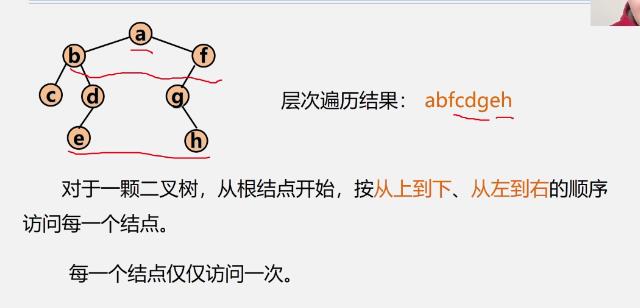
-
算法思路

-
算法描述
使用顺序循环队列
队列类型定义如下:
typedef struct BTNode data[MaxSize]; //存放队中元素 int front, rear; //队头和队尾指针 SqQueue; //顺序循环队列类型二叉树层次遍历算法:
void LevelOrder(BTNode *b) BTNode *p; SqQueue *qu; //初始化队列 enQueue(qu,b); //根结点指针进入队列 while(!QueueEmpty(qu)) //队不为空,则循环 deQueue(qu,p); //出队结点p printf("%c",p->data); //访问结点p if(p->lchild!=NULL) enQueue(qu,p->lchild); //有左孩子时令其进队 if(p->rchild!=NULL) enQueue(qu,p->rchild); //有右孩子时令其进队
4.二叉树遍历算法的应用
建立二叉树的算法
按先序遍历序列建立二叉树的二叉链表

根据某个先序序列建立的树不是唯一的,如:
为避免重复的情况,可以增加空结点,用#代替

-
算法描述
Status CreateBiTree(BiTree &T) scanf(&ch); if(ch=="#") T=NULL; else if(!(T=(BiTNode*)malloc(sizeof(BiTNode)))) //T=new BiTNode; exit(OVERFLOW); T->data = ch; //生成根结点 CreateBiTree(T->lchild); //构造左子树 CreateBiTree(T->rchild); //构造右子树 return OK;
复制二叉树
-
算法思路

-
算法描述
int Copy(BiTree T, BiTree &NewT) if(T==NULL) //如果是空树返回0 NewT=NULL; return 0; else NewT=new BiTNode; NewT->data=T->data; Copy(T->lChild,NewT->lchild); Copy(T->rchild,NewT->rchild);
计算二叉树的深度
-
算法思想

-
算法描述
int Depth(BiTree T) if(T==NULL) return 0; else m=Depth(T->lchild); n=Depth(T->rchild); if(m>n) return (m+1); else return (n+1);
计算二叉树结点总数
-
算法思想

加1加的就是根结点
-
算法描述
int NodeCount(BiTree T) if(T==NULL) return 0; else return NodeCount(T->lchild)+NodeCount(T->rchild)+1;
计算二叉树叶子结点数
-
算法思想

-
算法描述
int LeafCount(BiTree T) if(T==NULL) //如果是空树返回0 return 0; if(T->lchild == NULL && T->rchild == NULL) return 1; //如果是叶子结点返回1 else return LeafCount(T->lchild) + LeafCount(T->rchild);
5.线索二叉树
-
why

-
可能的解决办法

-
回顾空指针域
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LoFYc38f-1637761025279)(https://cdn.jsdelivr.net/gh/xin007-kong/picture_new/img/20211008083920.png)]
-
利用二叉链表的空指针域
-
-
what

-
对二叉树按某种遍历次序使其变为线索二叉树的过程叫线索化
-
例

-

-
-
结点结构

typedef struct BiThrNode int data; int ltag,rtag; struct BiThrNode *lchild,*rchild; BiThrNode, *BiThrTree;
线索二叉树的存储
先序线索二叉树
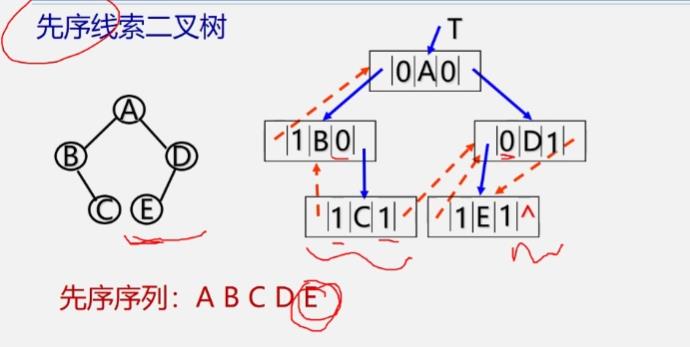
中序线索二叉树
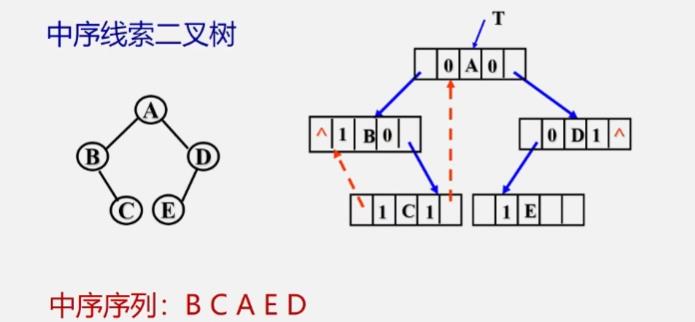
后序线索二叉树
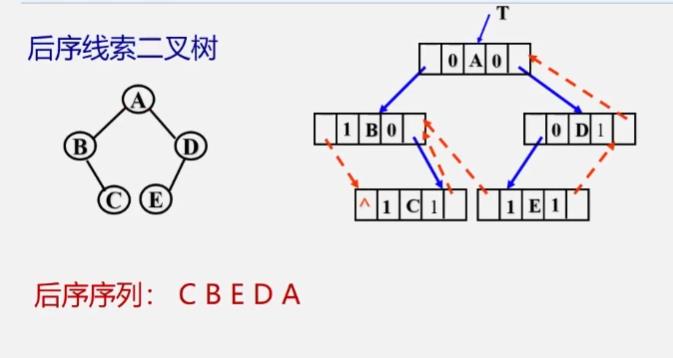
增设头结点

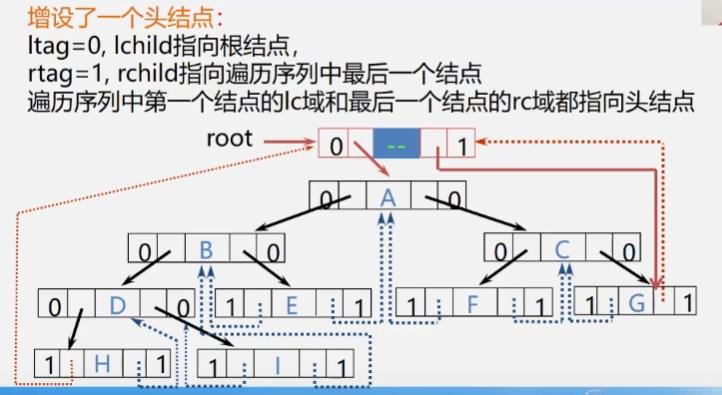
四.树和森林


1.树的存储结构
双亲表示法

-
C语言类型描述


孩子链表

-
C语言类型描述

-
再增加数据域

孩子兄弟表示法(二叉树表示法、二叉链表表示法)

-
例子
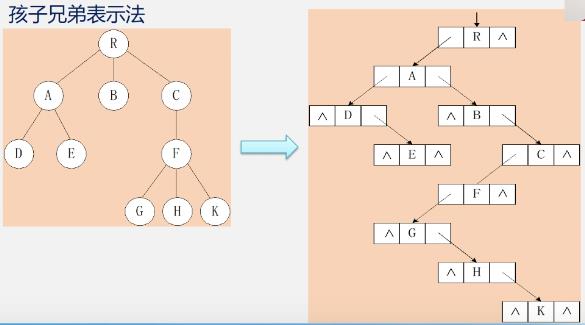
2.树与二叉树的转换
树转为二叉树

-
例

-
规律

-
例
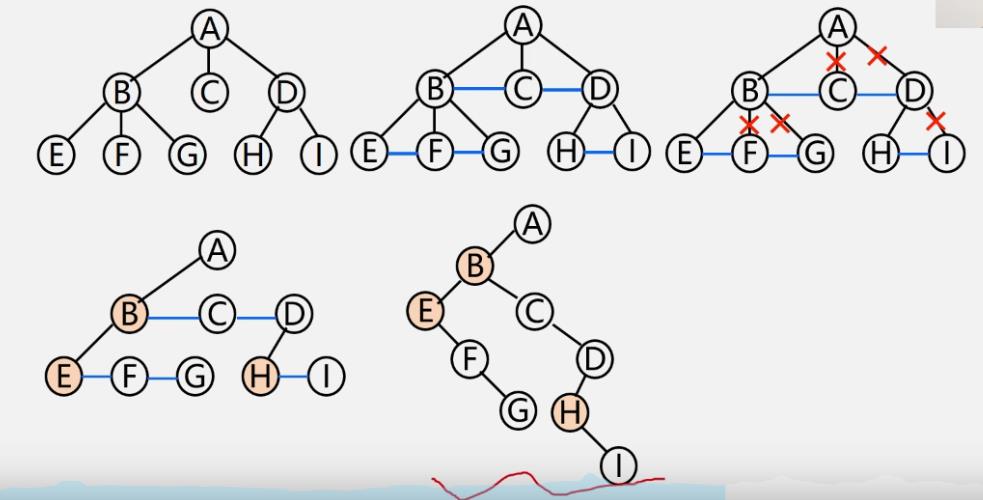
二叉树转为树

-
例

3,森林与二叉树的转换(二叉树与多棵树之间的关系)
森林转二叉树

-
例

二叉树转为森林

-
例

4.树与森林的遍历
树的遍历(三种方式)

森林的遍历

-
先序遍历

-
中序遍历

-
例
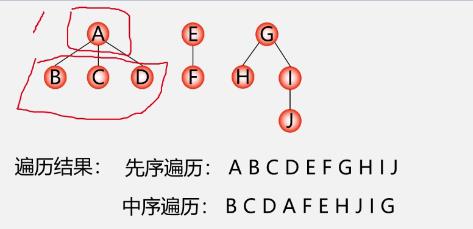
五.哈夫曼树
1.引入
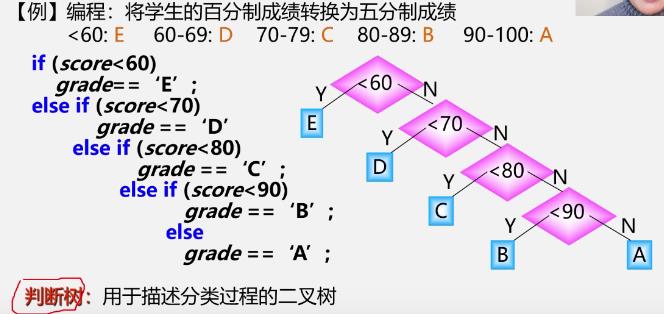

-
优化
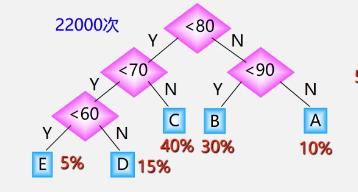

-
哈夫曼树

2.基本概念
路径、路径长度、权
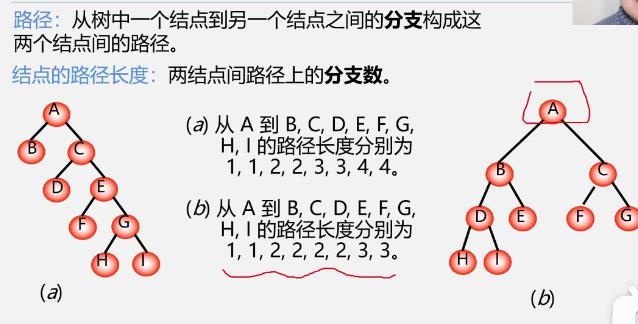
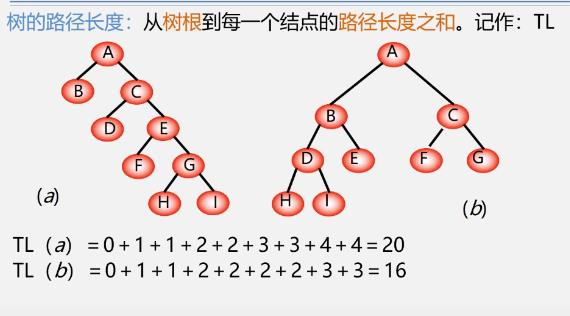
结点数目相同的二叉树中,完全二叉树是路径长度最短的二叉树

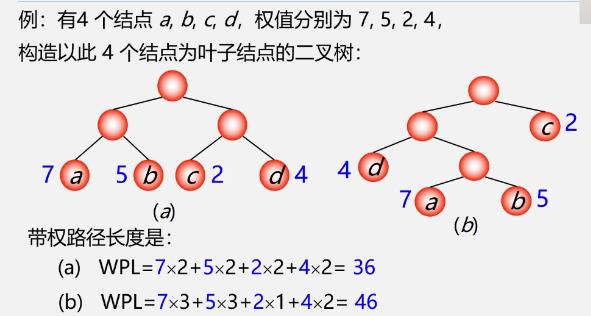
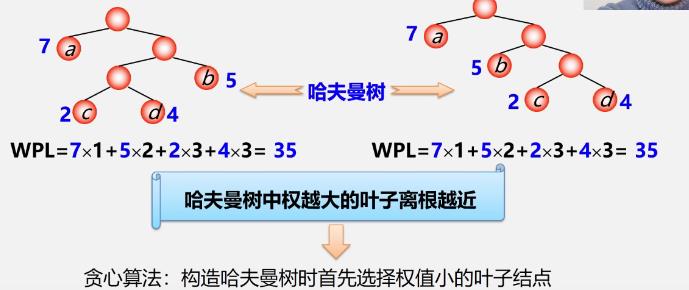
哈夫曼树

-
例
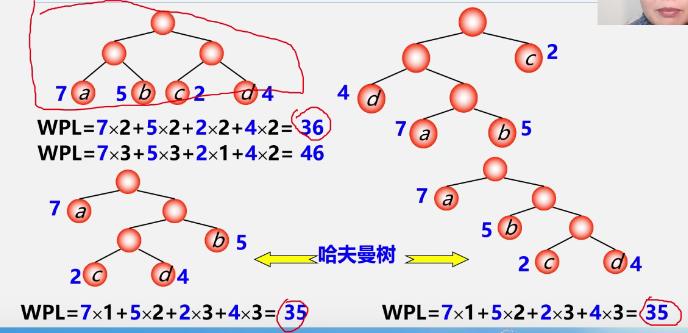
哈夫曼树特点
- 满二叉树不一定是最优二叉树(哈夫曼树)
- 哈夫曼树中权越大的叶子离根越近
- 具有相同带权结点的哈夫曼树不唯一
3.哈夫曼树的构造算法
C语言实现:
https://tyrantlucifer.com/44.html
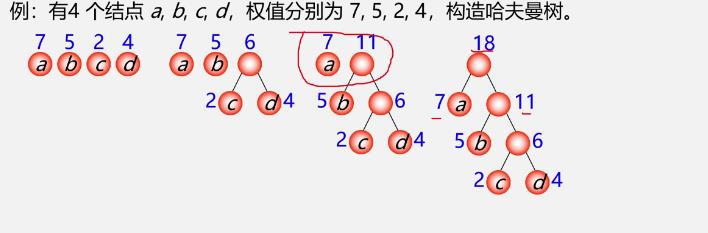
哈夫曼算法(构造哈夫曼树的方法)

-
例

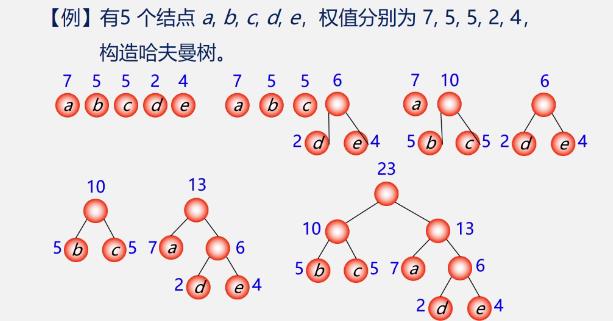
-
例
哈夫曼算法特点

哈夫曼树构造算法的实现
-
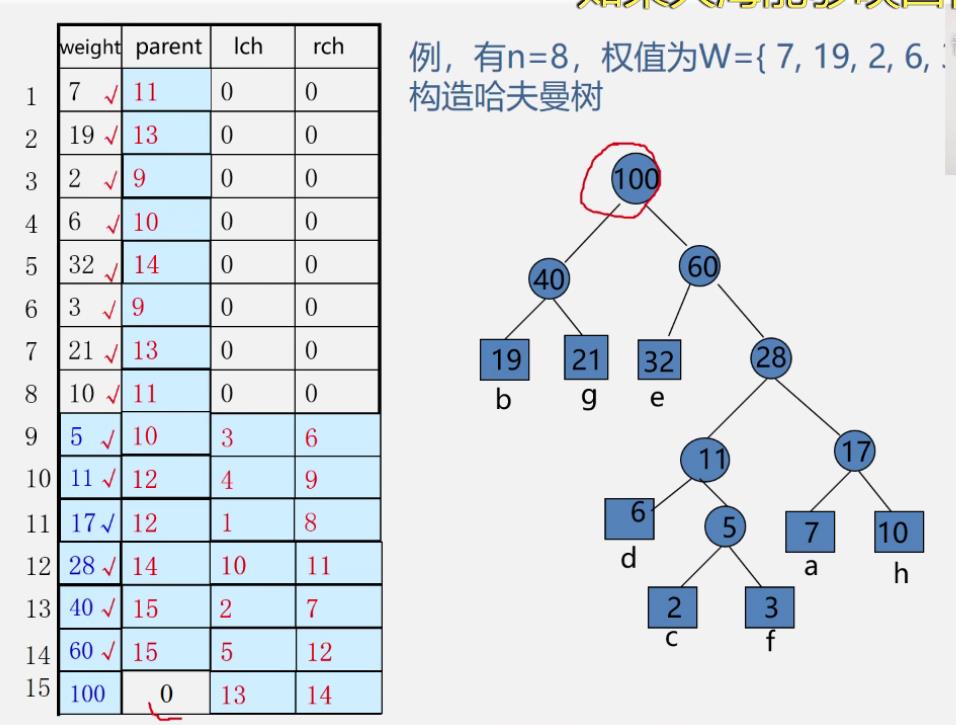
顺序存储结构

-
例
-
算法实现

-
代码实现
void CreatHuffmanTree(HuffmanTree HT,int n)//构造哈夫曼树--哈夫曼算法 if(n<=1) return; m=2*n-1; //数组共2n-1个元素 HT = new HTNode[m+1]; //0号单元未用,HT[m]表示根结点 for(i=1;i<=m;++i) //将2n-1个元素的lch、rch、parent置为0 HT[i].lch=0; HT[i].rch=0; HT[i].parent=0; for(i=1;i<=n;++i) cin>>HT[i].weight;//输入前n个元素的weight值 //初始化结束,下面开始建立哈夫曼树 for(i=n+1;i<=m;i++) //合并产生n-1个结点--构造Huffman树 Select(HT,i-1,s1,s2); //在HT[k](1≤k≤i-1)中选择两个其双亲域为0且权值最小的结点,并返回它们在HT中的序号s1和s2 HT[s1].parent=i; HT[s2].parent=i; //表示从F中删除s1,s2 HT[i].lch=s1; HT[i].rch=s2; //s1,s2分别作为i的左右孩子 HT[i].weight=HT[s1].weight+HT[s2].weight; //i的权值为左右孩子权值之和
-
-
例
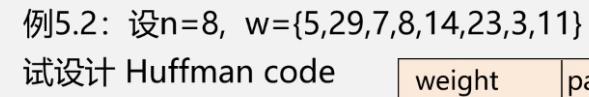
- 初始化
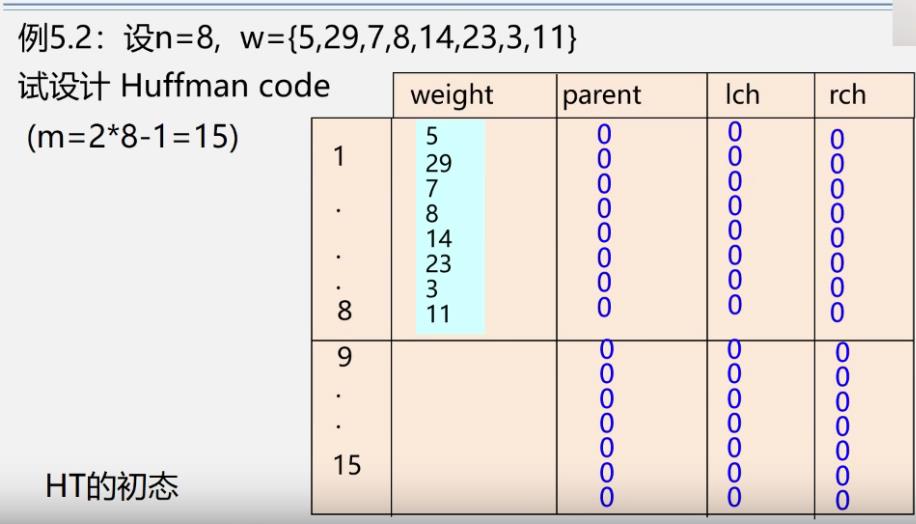
-
构造哈夫曼树
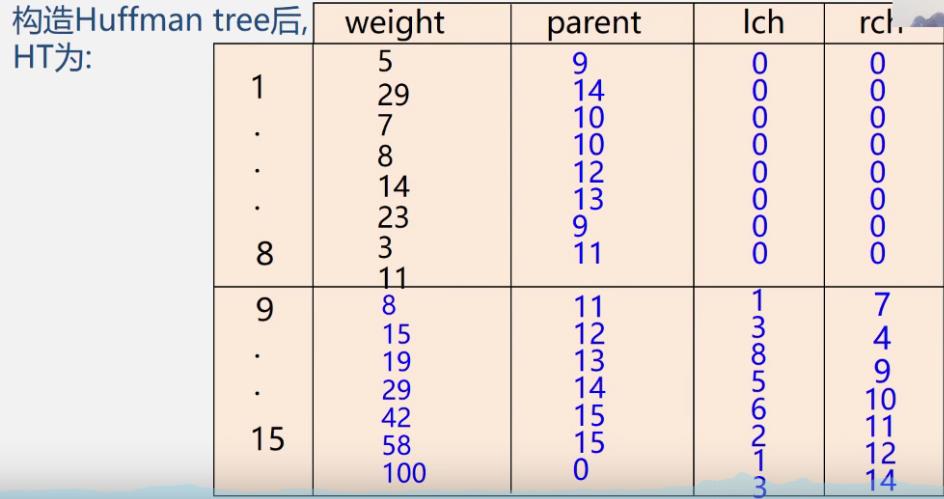
哈夫曼树的应用–哈夫曼编码
- 引入
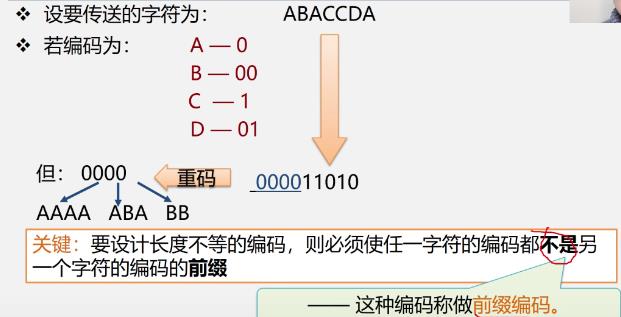

-
例
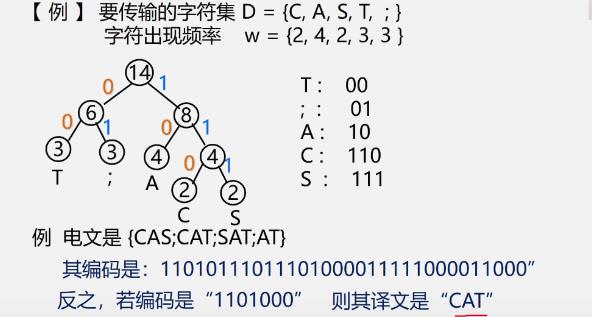
哈夫曼编码的性质
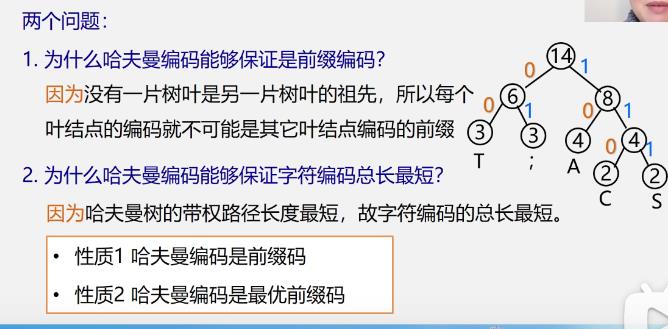
-
例54

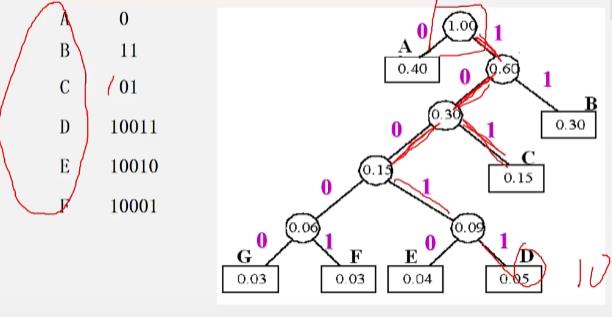
哈夫曼编码的算法实现
-
例
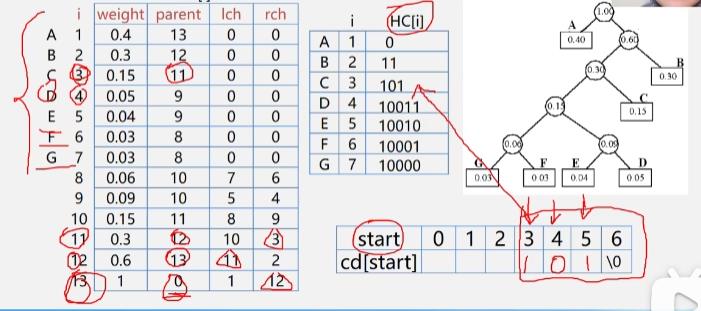
-
算法描述

4.哈夫曼树的应用
文件的编码和解码
-
引入
以上是关于数据结构与算法学习笔记 树的主要内容,如果未能解决你的问题,请参考以下文章