浅谈欧拉函数复习

Posted 2020-11-21 wzxbeliever

浅谈欧拉函数【复习】

定义：

φ(n)表示小于n的正整数中和n互质的个数;

性质：

1.积性函数：φ(n×m)=φ(n)×φ(m)（感性理解）

2.a^φ(n)^≡1（mod n)，当且仅当gcd(a,n)==1（感性理解）

3.[1,n]中与n互质的数的和为n×φ(n)/2

4.Σφ(d)=n,其中(d|n)（感性理解）

5.φ(p^a^)=p^a^-p^a-1^,其中(p为素数,a为正整数)

证明：

这里插入个游戏：

问题：求正整数3^83^的最后两位数

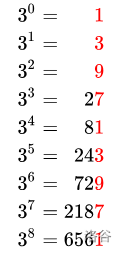
回到正题

一：√n求单个数的欧拉函数值：、

根据性质五：

code：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MAXN = 1e7 + 10;
int p, ans = 1, N;
void GetPhi() {
    for(int i = 2; i * i <= p; i++) {
        if(p % i == 0) {
            int now = i - 1; p /= i;
            while(p % i == 0) now = now * i, p /= i;
            ans = ans * now;
        }
    }
    if(p != 1) ans *= (p - 1); 
}
int main() {
    cin >> p; N = p;
    GetPhi();
    cout << ans;
    return 0;
}

二：线性塞欧拉函数

以下就是用到的性质

性质一：

φ(p)=p-1，当且仅当p为素数时

性质二：

若p不为i的约数且p为素数

则φ(i?p)=φ(i)?φ(p)

=φ(i?p)=φ(i)?(p?1)

这一步同时利用了性质1和欧拉函数的积性

性质3

若p是i的约数且p为素数，

则φ(i?p)=φ(i)?p

这个根据最开始的性质五可以得到

part code by wzxbeliever：

void init(){
    phi[1]=1;
    for(ri i=2;i<=n;i++){
        if(!vis[i])prime[++tot]=i,phi[i]=i-1;
        for(ri j=1;j<=tot&&i*prime[j]<=n;j++){
            vis[i*prime[j]]=1;
            if(!(i%prime[j])){phi[i*prime[j]]=phi[i]*prime[j];break;}
            else phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
}

光说不用等于放屁

例题一：

https://www.luogu.org/problem/P2158

分析：

由图观察发现能被看到的点当且仅当gcd(i,j)==1,

注意看图的时候将两点间空格看成一格，不要将点看成一格

所以问题转化为互质的点对有多少个

这里很容易想到欧拉函数

因为两边是对称的，只算一边就好了

code by wzxbeliever：

#include<bits/stdc++.h>
#define ll long long
#define il inline
#define ri register int
#define lowbit(x) x&(-x)
using namespace std;
const int maxn=40005;
int n,tot;
ll ans;
bool vis[maxn];
int phi[maxn],prime[maxn];
il void init(){
    phi[1]=1; 
    for(ri i=2;i<=n;i++){
        if(!vis[i])prime[++tot]=i,phi[i]=i-1;
        for(ri j=1;j<=tot&&i*prime[j]<=n;j++){
            vis[i*prime[j]]=1;
            if(!(i%prime[j])){phi[i*prime[j]]=phi[i]*prime[j];break;}
            else phi[i*prime[j]]=phi[i]*(prime[j]-1);
        }
    }
}
int main(){
    scanf("%d",&n);
    if(n==1){printf("0
");return 0;}//注意特判0
    init();
    for(ri i=1;i<=n-1;i++)
    ans+=phi[i];
    ans<<=1;ans++;
    printf("%lld
",ans);
    return 0;
}

大体上就这么多了