欧拉函数 / 蒙哥马利快速幂 / 容斥

Posted 2021-02-05 liuyongliu

一：知识点

欧拉函数参考1

浅谈欧拉函数参考2

欧拉函数的定义:

    在数论中，对于正整数N,少于或等于N ([1,N]),且与N互质（即gcd为1）的正整数(包括1)的个数，记作φ(n)。

　    　

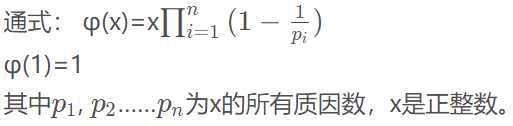
欧拉函数的延伸:

　　小于或等于n的数中，与n互质的数的总和为：φ(x) * x / 2  (n>1)。

欧拉函数φ(x)模板：

ll Euler(int n)//即求φ(x)
{
    ll ret=n;
    for(int i=2;i<=sqrt(n);i++)
     if(n%i==0)
      {
        ret=ret/i*(i-1);//先进行除法防止溢出(ret=ret*(1-1/p(i)))
        while(n%i==0)
          n/=i;
     }
    if(n>1)
          ret=ret/n*(n-1);
        return ret;
}

蒙哥马利快速幂：

　　蒙哥马利(Montgomery)幂模运算是快速计算a^b%k的一种算法，是RSA加密算法的核心之一。

算法模板：

ll Montgomery(ll base,ll exp)
{
    ll res = 1;
    while(exp)
    {
        if ( exp&1 )
            res = (res*base) % mod;
        exp >>= 1;
        base = (base*base) % mod;
    }
    return res;
}

容斥原理参考：(其证明参考)

　　实用：若gcd(n,i) == 1,那么gcd(n,n-i)==1

/*************************************************************************************************************************************/

二：牛客例题：小a与黄金街道

时间限制：C/C++ 1秒，其他语言2秒
空间限制：C/C++ 32768K，其他语言65536K
64bit IO Format: %lld

题目描述 

小a和小b来到了一条布满了黄金的街道上。它们想要带几块黄金回去，然而这里的城管担心他们拿走的太多，于是要求小a和小b通过做一个游戏来决定最后得到的黄金的数量。
游戏规则是这样的：
假设道路长度为$\mathrm{n米(左端点为0，右端点为n)，同时给出一个数k(下面会提到k的用法)设小a初始时的黄金数量为A，小b初始时的黄金数量为B小a从1出发走向n?1，小b从n?1出发走向1，两人的速度均为1m/s假设某一时刻(必须为整数)小a的位置为x，小b的位置为y，若gcd(n,x)=1且gcd(n,y)=1，那么小a的黄金数量A会变为A?k^x(kg)，小b的黄金数量B会变为B?k^y(kg)当小a到达n?1时游戏结束小a想知道在游戏结束时A+B的值答案对1e9+7取模}$

输入描述:

一行四个整数$\mathrm{n,k,A,B}$

输出描述:

输出一个整数表示答案

示例1

输入

4 2 1 1

输出

32

说明

初始时$\mathrm{A=1,B=1}$

第一个时刻如图所示，小a在$\mathrm{1，小b在3，满足条件，此时A=1?21=2,B=1?23=8A=1?21=2,B=1?23=8}$

 

第二个时刻小a在$\mathrm{2，小b在2，不满足条件}$

 

第三个时刻小a在$\mathrm{33，小b在11，满足条件，此时A=2?23=16,B=8?21=16A=2?23=16,B=8?21=16}$

此时游戏结束$\mathrm{A=2?23=16,B=8?21=16A=2?23=16,B=8?21=16}$

$\mathrm{A+B=32}$

示例2

输入

5 1 1 1

输出

2

备注:

保证 $\mathrm{3?n?1e8 , 1? A, B, k ?1e13}$

 AC代码：

/***********************************************/
ll Montgomery(ll base,ll exp)//base 底数，exponential　指数，mod 模
{
    ll res = 1;
    while(exp)
    {
        if ( exp&1 )
            res = (res*base) % mod;
        exp >>= 1;
        base = (base*base) % mod;
    }
    return res;
}

 ll Euler(int n)
{
    ll ret=n;
    for(int i=2;i<=sqrt(n);i++)
     if(n%i==0)
      {
        ret=ret/i*(i-1);//先进行除法防止溢出(ret=ret*(1-1/p(i)))
        while(n%i==0)
          n/=i;
     }
    if(n>1)
          ret=ret/n*(n-1);
        return ret;
}
 
int main()
{
    ll k,A,B;
    int n;
    cin>>n>>k>>A>>B;
    ll a=Euler(n)*n/2;
 
    ll p=Montgomery(k,a);
    cout<<(p*(A+B)%mod)%mod<<endl;
    return 0;
}