快速排序，归并排序，堆排序的数组和单链表实现

Posted 2020-11-21 fswhq

原文链接:https://www.cnblogs.com/DarrenChan/p/8807112.html

这三个排序的时间复杂度都是O(nlogn)，所以这里放到一起说。

回到顶部

1. 快速排序#

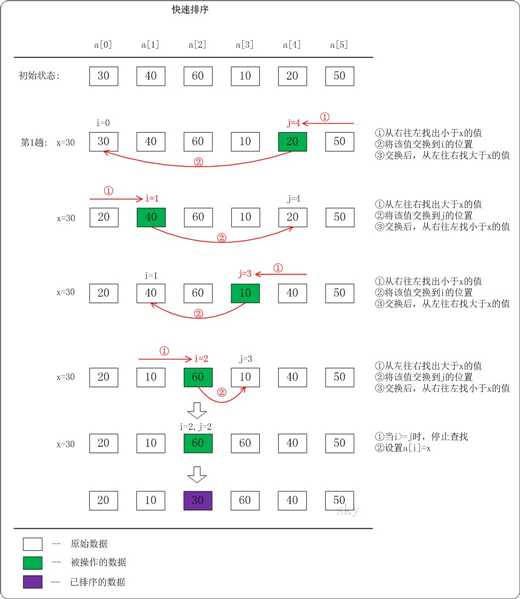
快速排序（英语：Quicksort），又称划分交换排序（partition-exchange sort），通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。

步骤为：

1. 从数列中挑出一个元素，称为"基准"（pivot），
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区结束之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会结束，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

• 最优时间复杂度：O(nlogn)
• 最坏时间复杂度：O(n2)
• 稳定性：不稳定

从一开始快速排序平均需要花费O(n log n)时间的描述并不明显。但是不难观察到的是分区运算，数组的元素都会在每次循环中走访过一次，使用O(n)的时间。在使用结合（concatenation）的版本中，这项运算也是O(n)。

在最好的情况，每次我们运行一次分区，我们会把一个数列分为两个几近相等的片段。这个意思就是每次递归调用处理一半大小的数列。因此，在到达大小为一的数列前，我们只要作log n次嵌套的调用。这个意思就是调用树的深度是O(log n)。但是在同一层次结构的两个程序调用中，不会处理到原来数列的相同部分；因此，程序调用的每一层次结构总共全部仅需要O(n)的时间（每个调用有某些共同的额外耗费，但是因为在每一层次结构仅仅只有O(n)个调用，这些被归纳在O(n)系数中）。结果是这个算法仅需使用O(n log n)时间。

数组实现#

public class QuickSort {
    public static void main(String[] args) {
        int[] a = { 1, 2, 4, 5, 7, 4, 5, 3, 9, 0 };
        quickSort(a, 0, a.length - 1);
        System.out.println(Arrays.toString(a));
    }

    private static void quickSort(int[] a, int low, int high) {
        if(low >= high){
            return;
        }
        
        int cur1 = low;
        int cur2 = high;
        int temp = a[low];
        
        while(cur1 < cur2){
            while(cur1 < cur2 && a[cur2] > temp){
                cur2--;
            }
            a[cur1] = a[cur2];
            while(cur1 < cur2 && a[cur1] <= temp){
                cur1++;
            }
            a[cur2] = a[cur1];
        }
        
        a[cur1] = temp;
        quickSort(a, low, cur1 - 1);
        quickSort(a, cur1 + 1, high);
    }
}

单链表实现#

在一般实现的快速排序中，我们通过首尾指针来对元素进行切分，下面采用快排的另一种方法来对元素进行切分。否则的话，单链表快排不方便，因为没有索引，不好从后往前遍历。

我们只需要两个指针p1和p2，这两个指针均往next方向移动，移动的过程中保持p1之前的key都小于选定的key，p1和p2之间的key都大于选定的key，那么当p2走到末尾时交换p1与key值便完成了一次切分。

图示如下：

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class QuickSortList{
    public ListNode sortList(ListNode head) {
       //采用快速排序
       quickSort(head, null);
       return head;
    }

    public static void quickSort(ListNode head, ListNode end) {
        if(head == end){
            return;
        }
        ListNode p1 = head, p2 = head.next;

        //走到末尾才停
        while (p2 != end) {

            //大于key值时，p1向前走一步，交换p1与p2的值
            if (p2.val < head.val) {
                p1 = p1.next;

                int temp = p1.val;
                p1.val = p2.val;
                p2.val = temp;
            }
            p2 = p2.next;
        }

        //当有序时，不交换p1和key值
        if (p1 != head) {
            int temp = p1.val;
            p1.val = head.val;
            head.val = temp;
        }

        quickSort(head, p1);
        quickSort(p1.next, end);
    }
}

可以在https://leetcode-cn.com/problems/sort-list/description/进行测试。 

回到顶部

2. 归并排序#

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。

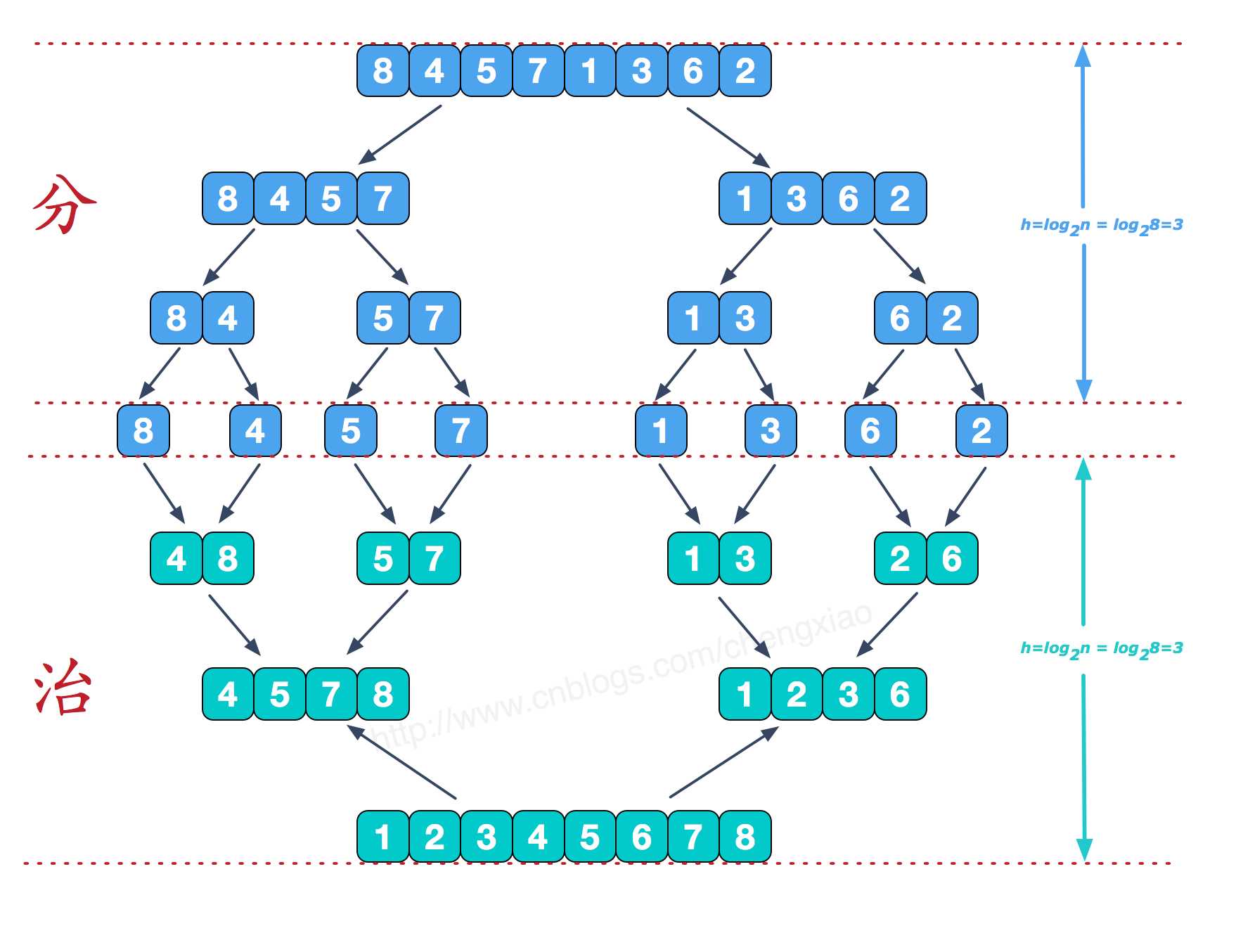
分而治之

可以看到这种结构很像一棵完全二叉树，本文的归并排序我们采用递归去实现（也可采用迭代的方式去实现）。分阶段可以理解为就是递归拆分子序列的过程，递归深度为log₂n。

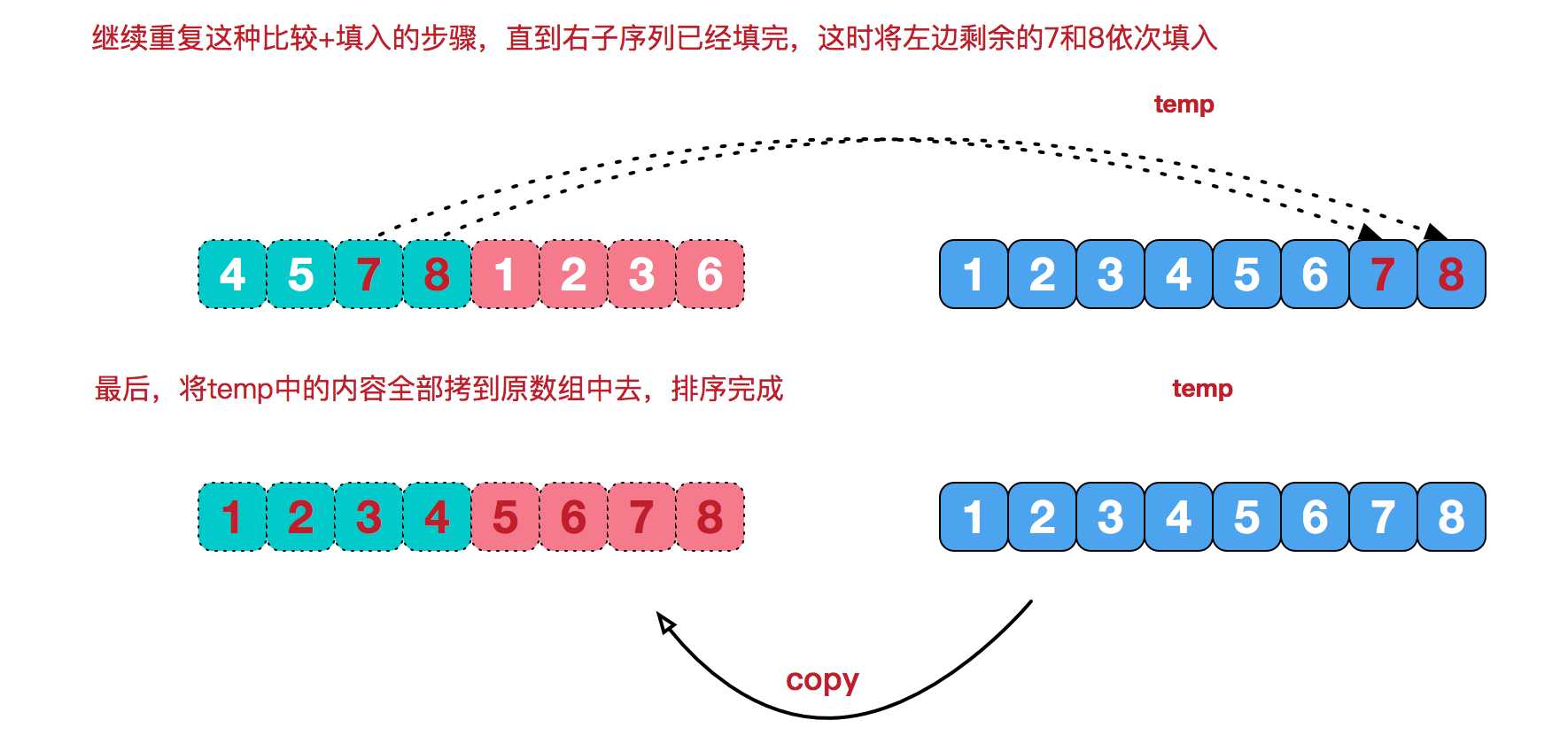
再来看看治阶段，我们需要将两个已经有序的子序列合并成一个有序序列，比如上图中的最后一次合并，要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列，合并为最终序列[1,2,3,4,5,6,7,8]，来看下实现步骤。

数组实现#

public class MergeSort {
    public static void main(String[] args) {
        int[] arr = { 9, 8, 7, 6, 5, 4, 3, 2, 1 };
        sort(arr, 0, arr.length - 1);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int[] arr, int left, int right) {
        if(left < right){
            int middle = (left + right) / 2;
            sort(arr, left, middle);//对左子序列排序
            sort(arr, middle + 1, right);//对右子序列排序
            merge(arr, left, right, middle);
        }
    }

    private static void merge(int[] arr, int left, int right, int middle) {
        int[] temp = new int[arr.length];
        int i = left;//左指针
        int j = middle + 1;//右指针
        int k = i;//这是temp的指针
        while(i <= middle && j <= right){
            if(arr[i] < arr[j]){
                temp[k++] = arr[i++];
            }else{
                temp[k++] = arr[j++];
            }
        }
        
        //处理剩余的字符
        while(i <= middle){
            temp[k++] = arr[i++];
        }
        
        while(j <= right){
            temp[k++] = arr[j++];
        }
        
        // 将临时数组中的内容存储到原数组中
        while (left <= right) {
            arr[left] = temp[left++];
        }
    }
}

单链表实现#

归并排序应该算是链表排序最佳的选择了，保证了最好和最坏时间复杂度都是nlogn，而且它在数组排序中广受诟病的空间复杂度在链表排序中也从O(n)降到了O(1)。

归并排序的一般步骤为：

1. 将待排序数组（链表）取中点并一分为二；
2. 递归地对左半部分进行归并排序；
3. 递归地对右半部分进行归并排序；
4. 将两个半部分进行合并（merge），得到结果。

首先用快慢指针(快慢指针思路，快指针一次走两步，慢指针一次走一步，快指针在链表末尾时，慢指针恰好在链表中点)的方法找到链表中间节点，然后递归的对两个子链表排序，把两个排好序的子链表合并成一条有序的链表。

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode(int x) { val = x; }
 * }
 */
class MergeSortList{
    public ListNode sortList(ListNode head) {
        
        if(head == null || head.next == null){
            return head;
        }

        ListNode mid = getMid(head);
        ListNode right = mid.next;
        mid.next = null;//将两个链表分开
        ListNode node = merge(sortList(head), sortList(right));
        return node;
    }
    
    /**
     * 获取链表的中间结点，偶数时取中间第一个
     * @param head
     * @return
     */
    public ListNode getMid(ListNode head){
        if(head == null){
            return head;
        }
        ListNode fast = head;//快指针
        ListNode slow = head;//慢指针
        
        while(fast.next != null && fast.next.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        
        return slow;
    }
    
    /**
     * 归并两个有序的链表
     * 把另一个链表插入到当前链表中
     * @param head1
     * @param head2
     * @return
     */
    private ListNode merge(ListNode head1, ListNode head2){
        if(head1 == null || head2 == null){
            return head1 != null ? head1 : head2;
        }
        ListNode head = head1.val < head2.val ? head1 : head2;
        ListNode cur1 = head == head1 ? head1 : head2;
        ListNode cur2 = head == head1 ? head2 : head1;
        ListNode pre = null;//用来记录cur1的上一个
        ListNode next = null;//用来记录cur2的下一个
        while(cur1 != null && cur2 != null){
            if(cur1.val <= cur2.val){//这里一定要有=，否则一旦cur1的value和cur2的value相等的话，下面的pre.next会出现空指针异常
                pre = cur1;
                cur1 = cur1.next;
            }else{
                next = cur2.next;
                pre.next = cur2;
                cur2.next = cur1;
                pre = cur2;
                cur2 = next;
            }
        }
        pre.next = cur1 == null ? cur2 : cur1;
        return head;
    }
}

可以在https://leetcode-cn.com/problems/sort-list/description/进行测试。 

归并排序还可以不用递归，具体参考博客：http://www.cnblogs.com/weiyinfu/p/8546080.html

回到顶部

3. 堆排序#

　　堆排序是利用堆这种数据结构而设计的一种排序算法，堆排序是一种选择排序，它的最坏，最好，平均时间复杂度均为O(nlogn)，它也是不稳定排序。首先简单了解下堆结构。

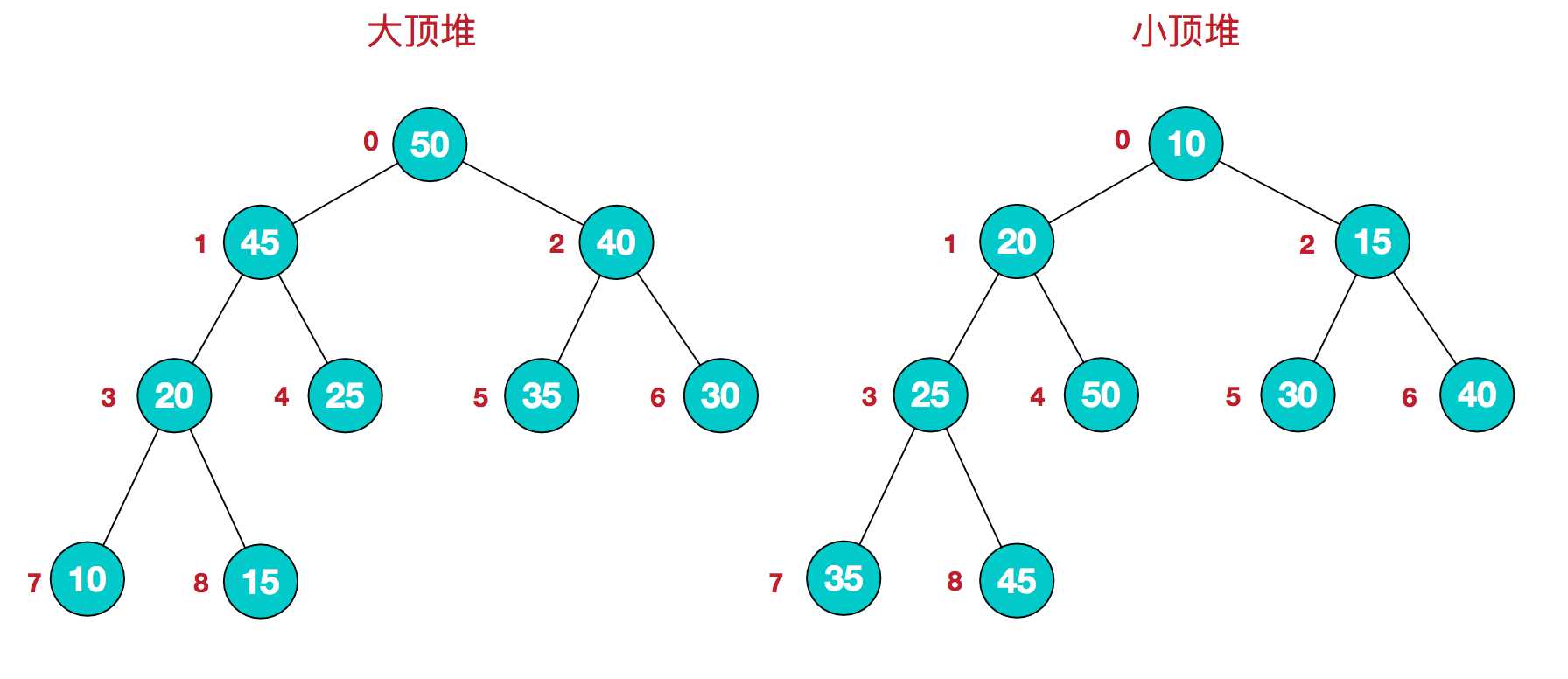
　　堆是具有以下性质的完全二叉树：每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆；或者每个结点的值都小于或等于其左右孩子结点的值，称为小顶堆。如下图：

同时，我们对堆中的结点按层进行编号，将这种逻辑结构映射到数组中就是下面这个样子

该数组从逻辑上讲就是一个堆结构，我们用简单的公式来描述一下堆的定义就是：

大顶堆：arr[i] >= arr[2i+1] && arr[i] >= arr[2i+2]  

小顶堆：arr[i] <= arr[2i+1] && arr[i] <= arr[2i+2]  

ok，了解了这些定义。接下来，我们来看看堆排序的基本思想及基本步骤：

堆排序的基本思想是：将待排序序列构造成一个大顶堆，此时，整个序列的最大值就是堆顶的根节点。将其与末尾元素进行交换，此时末尾就为最大值。然后将剩余n-1个元素重新构造成一个堆，这样会得到n个元素的次小值。如此反复执行，便能得到一个有序序列了。

步骤一 构造初始堆。将给定无序序列构造成一个大顶堆（一般升序采用大顶堆，降序采用小顶堆)。

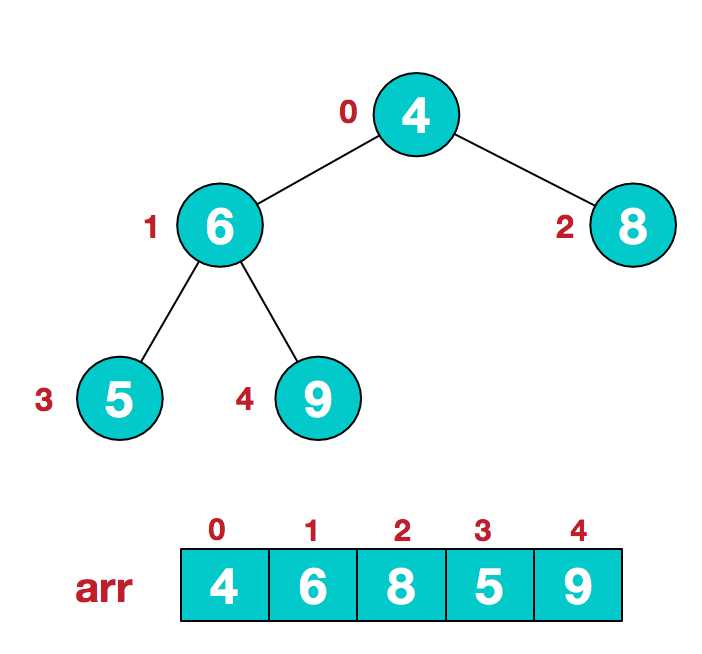
假设给定无序序列结构如下

此时我们从最后一个非叶子结点开始（叶结点自然不用调整，第一个非叶子结点 arr.length/2-1=5/2-1=1，也就是下面的6结点），从左至右，从下至上进行调整。

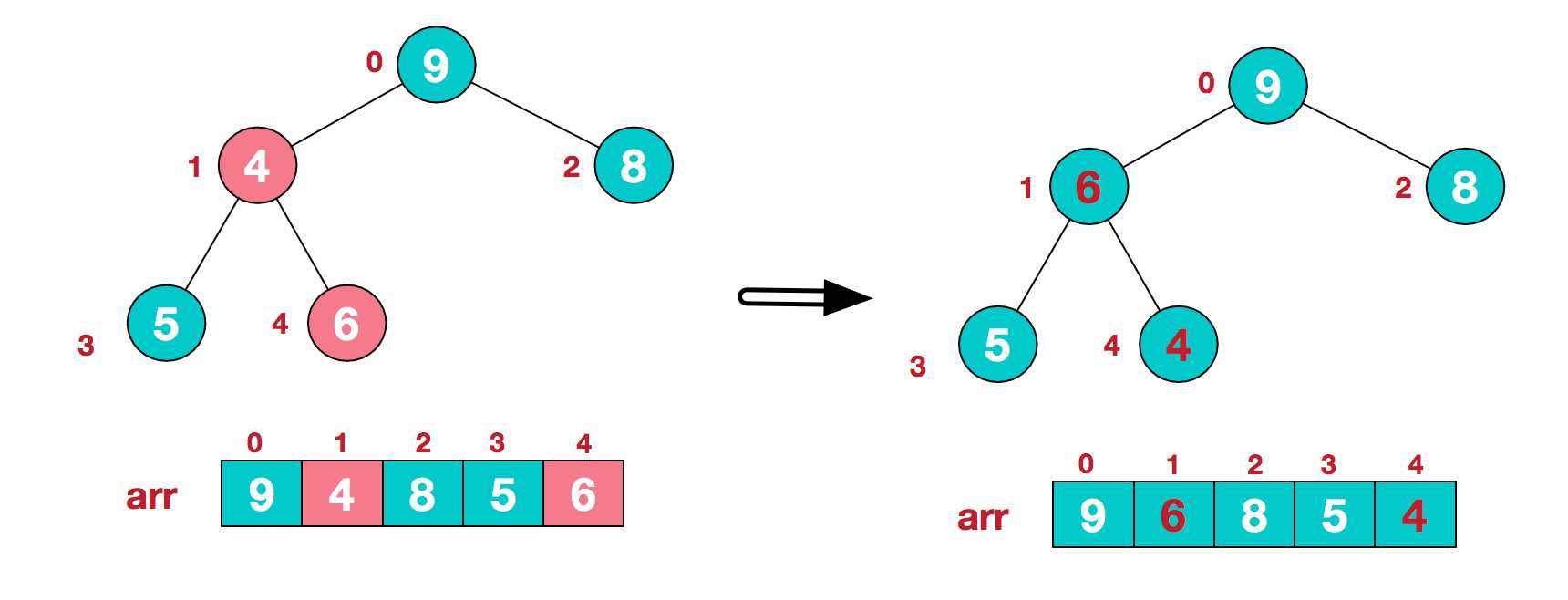
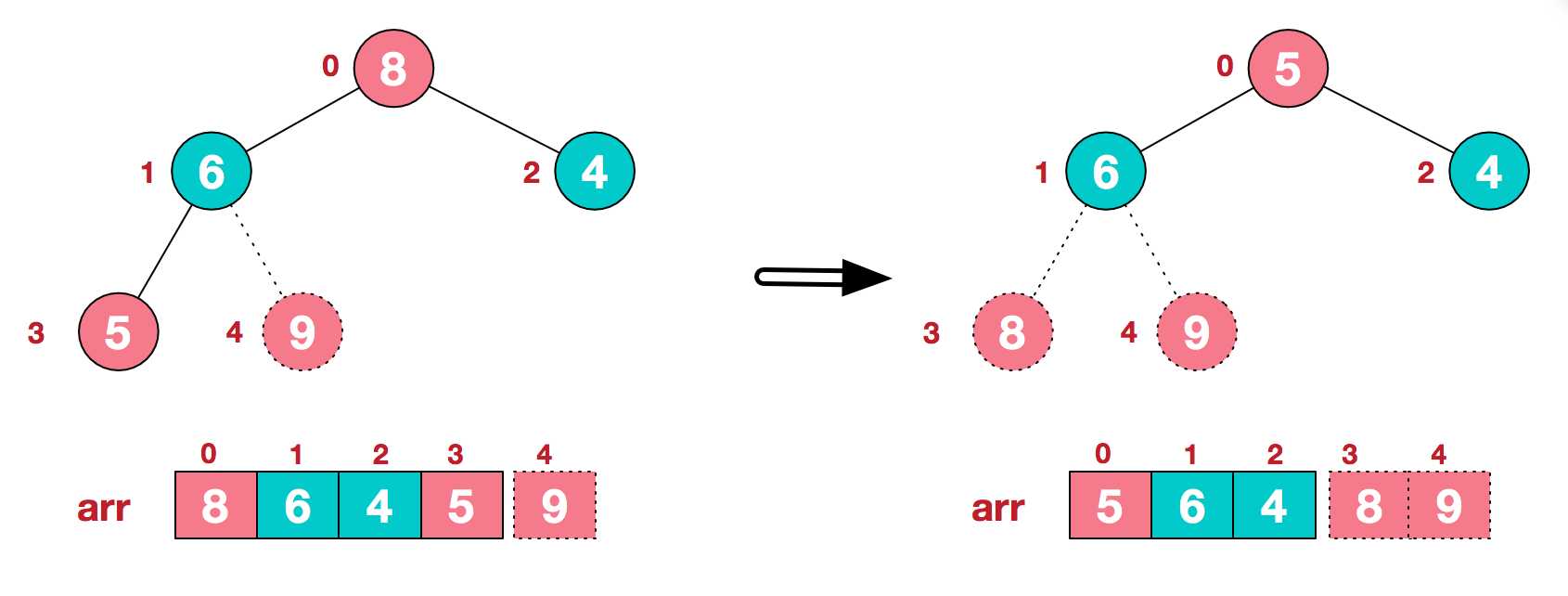
找到第二个非叶节点4，由于[4,9,8]中9元素最大，4和9交换。

这时，交换导致了子根[4,5,6]结构混乱，继续调整，[4,5,6]中6最大，交换4和6。

此时，我们就将一个无需序列构造成了一个大顶堆。

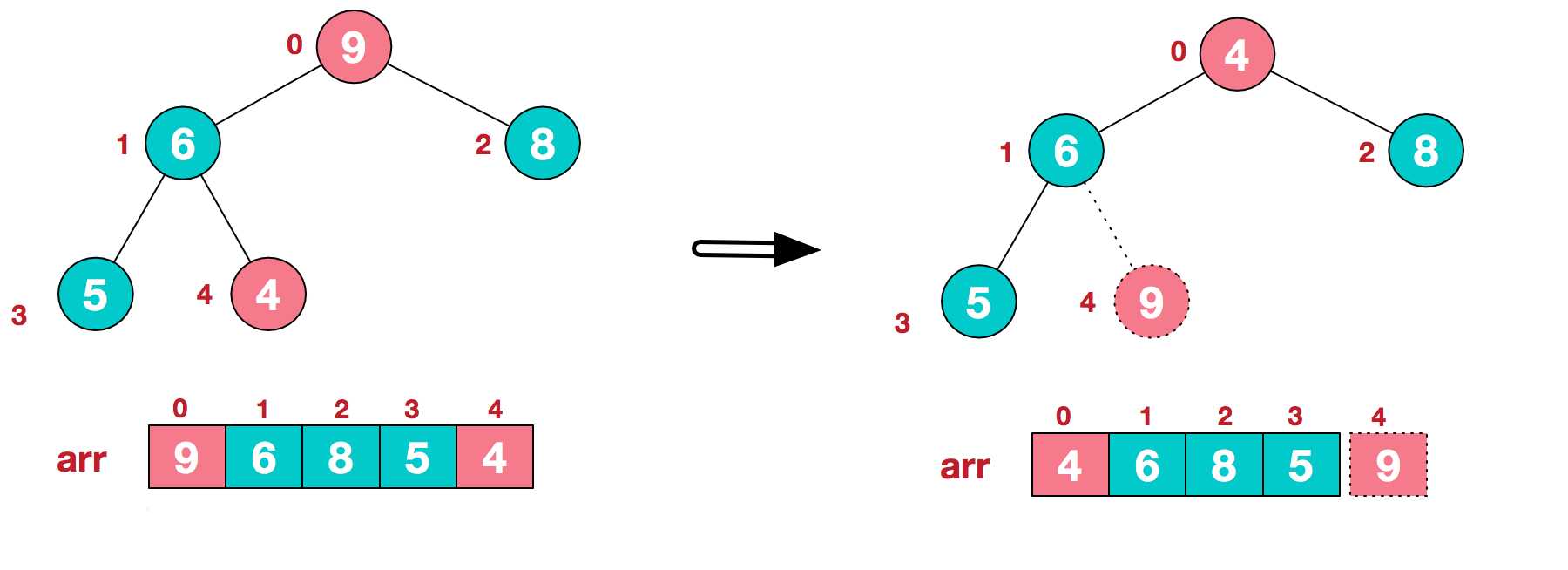
步骤二 将堆顶元素与末尾元素进行交换，使末尾元素最大。然后继续调整堆，再将堆顶元素与末尾元素交换，得到第二大元素。如此反复进行交换、重建、交换。

将堆顶元素9和末尾元素4进行交换。

重新调整结构，使其继续满足堆定义。

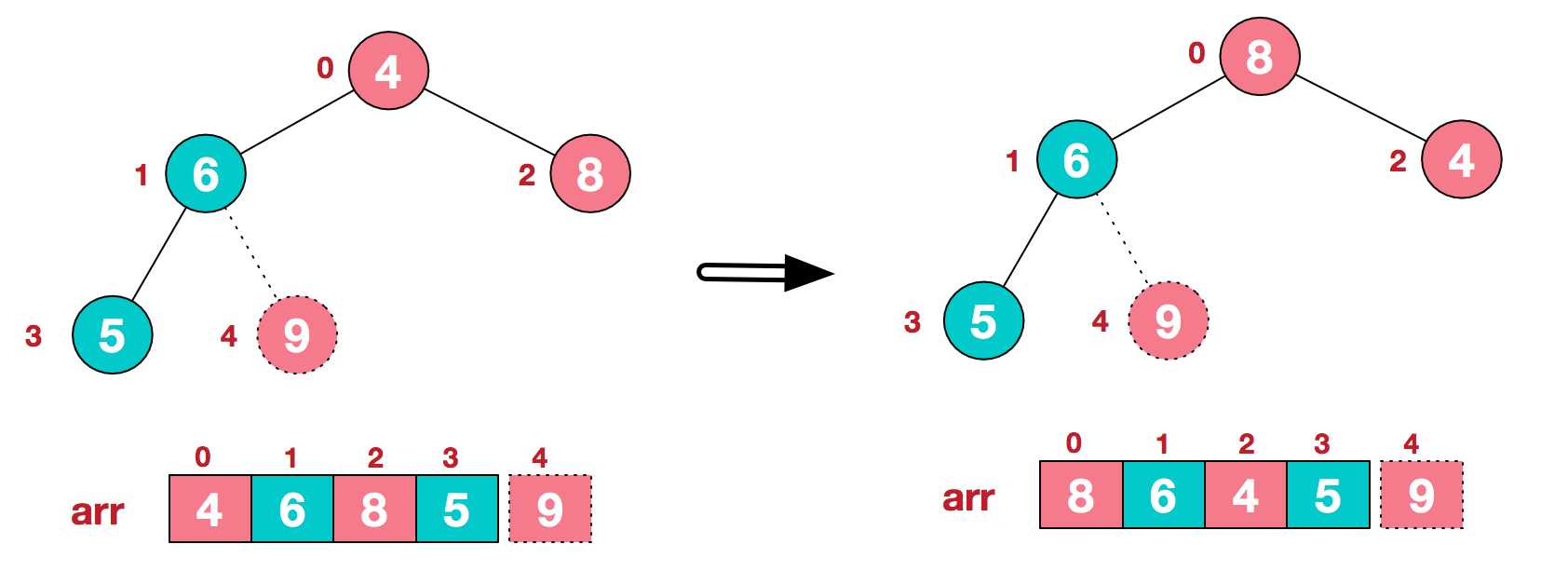
再将堆顶元素8与末尾元素5进行交换，得到第二大元素8。

后续过程，继续进行调整，交换，如此反复进行，最终使得整个序列有序

再简单总结下堆排序的基本思路：

　　a.将无需序列构建成一个堆，根据升序降序需求选择大顶堆或小顶堆;

　　b.将堆顶元素与末尾元素交换，将最大元素"沉"到数组末端;

　　c.重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整个序列有序。

数组实现#

public class HeapSort {
    public static void main(String[] args) {
        int[] arr = new int[] { 7, 8, 5, 9, 4, 6, 2, 1, 3 };
        sort(arr);
        System.out.println(Arrays.toString(arr));
    }

    public static void sort(int[] arr) {
        //1.先确定大顶堆
        for (int i = arr.length / 2 - 1; i >= 0; i--) {
            adjustHeap(i, arr, arr.length);
        }
        //2.交换并取出
        for (int j = arr.length - 1; j > 0; j--) {
            int temp = arr[j];
            arr[j] = arr[0];
            arr[0] = temp;

            adjustHeap(0, arr, j);
        }
    }

    private static void adjustHeap(int i, int[] arr, int length) {
        int temp = arr[i];

        for (int k = 2 * i + 1; k < length; k = 2 * k + 1) {
            if (k + 1 < length && arr[k] < arr[k + 1]) {//选取两个叶子节点中较大的那一个
                k++;
            }
            if (arr[k] > temp) {
                arr[i] = arr[k];
                i = k;
            }
        }
        arr[i] = temp;
    }
}

单链表实现#

暂时没有思路，欢迎补充交流。