排序算法

Posted 2020-11-21 zs-notes

　　排序是计算机程序设计的一种重要操作，它的功能是将一个数据元素（或记录）的任意序列，重新排列成一个按关键字有序的序列。下面主要对一些常见的排序算法做的介绍，并分析它们的时空复杂度。

　　常见排序算法：
　　1.冒泡排序
　　2.简单选择排序
　　3.直接插入排序
　　4.希尔排序
　　5.归并排序
　　6.快速排序
　　7.堆排序

　　

　　常见排序算法性能的比较：

　　

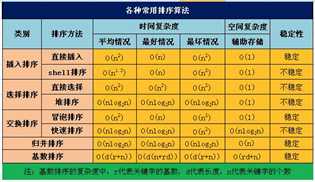
　　上图表中最后一列“稳定性”，是指如果在排序的序列中，存在前后相同的两个元素的话，排序前和排序后他们的相对位置不发生变化。

　　下面从冒泡排序开始逐一介绍：

　　1.冒泡排序

　　冒泡排序的基本思想是：设排序序列的记录个数为n，进行n-1次遍历，每次遍历从开始位置依次往后比较前后相邻元素，这样较大的元素往后移，n-1次遍历结束后，序列有序。

　　实现：

public class bubbleSort {   //冒泡排序法
     public static void main(String[] args) {
            int[] line = {24,36,12,25,3,67,55};
            maopao(line)  ;
     } 
     public static void maopao(int[] line) {
           for (int i = 0; i < line.length - 1; i++) {// 最多做line.length-1趟排序
                for (int j = i; j < line.length; j++) {
                     int temp = 0;
                     if (line[i] > line[j]) {  //相邻的两个比较
                           temp = line[i];
                           line[i] = line[j];
                           line[j] = temp;
                     }
                }
           }
           System.out.println(Arrays.toString(line));   //[3, 12, 24, 25, 36, 55, 67]
     }
}

　　分析：最佳情况下冒泡排序只需一次遍历就能确定数组已经排好序，不需要进行下一次遍历，所以最佳情况下，时间复杂度为** O(n) **。

　　最坏情况下冒泡排序需要n-1次遍历，第一次遍历需要比较n-1次，第二次遍历需要n-2次，...，最后一次需要比较1次，最差情况下时间复杂度为** O(n^2) **。

　　2.简单选择排序

　　简单选择排序的思想是：设排序序列的记录个数为n，进行n-1次选择，每次在n-i+1(i = 1,2,...,n-1)个记录中选择关键字最小的记录作为有效序列中的第i个记录。

　　实现：

public class selectionSort { 
     public static void main(String[] args) {
           int[] line = { 23, 17, 5, 8, 1, 25, 33 };
           selectSort(line);
     } // 思路：在每步中选择最小数来重新排列
　　 public static void selectSort(int[] line) {
        for (int i = 0; i < line.length - 1; i++) {
            int min = i;
            // 每次从未排序数组中找到最小值的坐标
            for (int j = i + 1; j < line.length; j++) {
                if (line[j] < line[min]) {
                    min = j;
                }
            }
            // 将最小值放在最前面
            if (min != i) {
                int temp = line[min];
                line[min] = line[i];
                line[i] = temp;
            }
        }
        System.out.println(Arrays.toString(line));
    }
}

　　分析：简单选择排序过程中需要进行的比较次数与初始状态下待排序的记录序列的排列情况** 无关。当i=1时，需进行n-1次比较；当i=2时，需进行n-2次比较；依次类推，共需要进行的比较次数是(n-1)+(n-2)+…+2+1=n(n-1)/2，即进行比较操作的时间复杂度为 O(n^2) ，进行移动操作的时间复杂度为 O(n) 。总的时间复杂度为 O(n^2) **。

　　3.直接插入排序