试述MSE,估计量方差,偏倚的含义以及三者间的关系?
Posted
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了试述MSE,估计量方差,偏倚的含义以及三者间的关系?相关的知识,希望对你有一定的参考价值。
无回答误差是指在调查中由于各种原因,调查人员没能够从入选样本的单元处获得所需要的信息,由于数据缺失造成估计量的偏误。这种情况一般发生在以人为调查对象的时候。无回答误差是一种重要的非抽样误差,对调查数据的质量起着重要影响。由于这种现象十分普遍,对估计量的危害也比较大,所以国际上对这方面的讨论一直比较激烈,目前这种讨论仍在继续。无回答产生于不同的情况,据此可以对无回答进行不同的分类。从内容上看,可以分为单元无回答和项目无回答。单元无回答指被调查单元没有参与或拒绝接受调查,他们交的是一份白卷。项目无回答指被调查单元虽然接受调查,但对其中的一些调查项目没有回答。与单元无回答相比,项目无回答或多或少地提供了一些信息。
从性质上看,可以分为有意无回答和无意无回答。有意无回答常常与调查内容有关,例如对调查内容敏感,或涉及个人隐私不愿意回答。无意无回答通常与调查内容无关,之所以出现是由于其他原因造成的,如被调查者生病或很忙,无法接受调查等。有意无回答对数据质量的影响很大,回答者和无回答者之间往往存在系统性差异。这种无回答不仅减少了有效样本量,造成估计量方差增大,而且会带来估计偏倚。无意无回答可以看成是随机的,这种无回答虽然会造成估计量方差增大,但通常认为不会带
1/4页
来估计偏倚。
当然,如果无回答产生于某个群体,而该群体与其他群体在目标变量方面存在数量差异,那么即便是无意无回答,也会造成估计量的偏倚。例如调查居民的旅游开支,不在家的人可能恰恰是经常外出旅游的。虽然这是无意无回答,但却会造成有偏估计。
二、无回答产生的原因及影响
如果把采集数据的过程划分为查找、接触和采访三个阶段,三个阶段都有可能出现无回答。
1、 查找阶段。调查人员无法找到被调查者,主要原因有地址不详、被调查者搬迁、被调查者不在现场、调查人员不熟悉地址等。
2、接触阶段。被调查者由于客观原因无法接受调查,如生病或没有时间;被调查者由于主观原因拒访,如对调查不感兴趣,出于安全考虑不让调查员入户等。
3、采访阶段。调查开始后被调查者对某些问题不愿提供答案、调查员由于粗心遗漏某些项目、由于某种原因调查中断等。
为了分析无回答的影响,可以假设总体由两个层组成。一个是回答层,如果这个层的单元被抽中,就可以得到回答;另一个是无回答层,采用相同抽样方式,如果这个层的单元被抽中,就
NNN,,无法得到回答。设分别为总体单元数、回答层单元数、10
RR,无回答层单元数。分别为总体回答率和无回答率,即 10
NN01NNN,, R,R,1010NN
2/4页
则总体均值 YRYRY,,1100
n从总体中抽取容量为n的简单随机样本,来自于回答层,1
ny来自于无回答层。根据回答单元计算出的样本均值为,它是01
y总体中回答层均值的无偏估计,即。于是用作为总体EyY(),111
均值的估计值,其偏倚为: Y
偏倚()()yEy,,,-Y=Y(RY+RY)=RYY() 1111100010
RYY(),010 相对偏倚()y,1Y
相同的方法可以得到总量估计的偏倚和相对偏倚分别为:
ˆˆ偏倚()()-NY=NRYYyNEy,,() 11010
RYY(),010ˆ相对偏倚(y), 1Y
由模型看出,导致无回答偏倚的原因主要来自于两个方面:
YY,一个是回答层与无回答层单位之间的数量差异;一个是无回10
R答率 0
YY,上述模型给我们一些启示:首先,如果,即回答单元10
与无回答单元目标变量的数量特征没有显著差异,可以看成无回答是由于一些随机因素引起的,这时问题尚不严重,因为不会引起估计偏倚。但是,由于无回答造成实际接受调查单元数目减少,会引起估计方差的增大,这时只要简单地增大样本量,使完成调
YY,查单元数目与调查方案要求相一致即可。其次,如果,仅10
Y与Y仅用回答数据进行估计就会产生偏倚,且的差异越大,估计10
偏倚就越大,这时降低无回答率就十分重要。最后,如果无法最
3/4页
终消灭无回答,就需要采取一些补救措施,通过对调查数据的调整,以减少由于无回答对估计带来的影响。
三、降低无回答的措施
1、问卷设计具有吸引力,容易引起被调查者参与的兴趣,并注意适当的长度。
2、在可能的条件下,充分利用调查组织者的权威性和社会影响力,激发被调查者的参与意识。
3、确定准确的调查方位,使调查员容易找到被调查者。
4、采取有助于消除被调查者冷漠、担心或怀疑的措施,如预先通知、调查前的解释说明及雇佣与被调查者熟悉的人做调查员。
5、注意调查员的挑选。调查员的身份与被调查者越接近,就越容易被对方接受。实践表明,大学生、居民委员会成员、下岗职工都是理想的非专职调查员人选。
6、作好调查员的培训,增强其责任心,提高其访问技巧。
7、注意调查过程的监控。
8、奖励措施。
9、再次调查。
10、替换被调查单元。 参考技术A 试述MSE,估计量方差,偏倚的含义以及三者间的关系?
估计偏差和方差
1.点估计
令 {x (1) ,...,x (m) } 是 m 个独立同分布(i.i.d.)的数据点。点估计(point esti-mator)或统计量(statistics)是这些数据的任意函数:
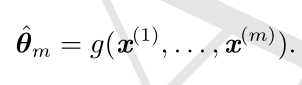
良好的估计量的输出会接近生成训练数据的真实参数 θ
点估计也可以指输入和目标变量之间关系的估计。我们将这种类型的点估计称为函数估计
2.偏差
估计的偏差被定义为:
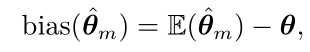
其中期望作用在所有数据(看作是从随机变量采样得到的)上,θ 是用于定义数据生成分布的 θ 的真实值
如果 bias( ? θ m ) = 0,那么估计量?θ m 被称为是无偏(unbiased),这意味着 E( ? θ m ) = θ。
如果 lim m→∞ bias( ? θ m ) = 0,那么估计量?θ m 被称为是渐近无偏(asymptotically unbiased),这意味着 lim m→∞ E( ? θ m ) = θ
3.方差和标准差
估计量的方差(variance)就是一个方差
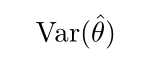
方差的平方根被称为标准差(standard error),记作SE( ? θ)
均值的标准差被记作
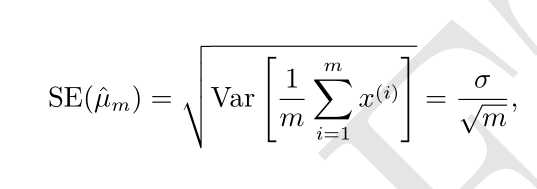
均值 ? μ m 为中心的 95% 置信区间是
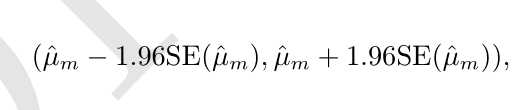
算法 A 比算法 B 好,是指算法 A 的误差的 95% 置信区间的上界小于算法 B的误差的 95% 置信区间的下界
均方误差
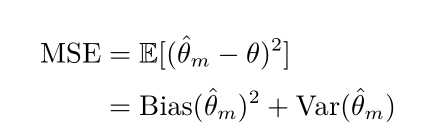
以上是关于试述MSE,估计量方差,偏倚的含义以及三者间的关系?的主要内容,如果未能解决你的问题,请参考以下文章
估计量|估计值|置信度|置信水平|非正态的小样本|t分布|大样本抽样分布|总体方差|