连续子数组的最大和

Posted 2020-11-19 zhibei

题目：输入一个整型数组，数组里有正数也有负数。数组中一个或连续多个整数组成一个子数组。求所有子数组的和的最大值。要求时间复杂度为O(n).

解题思路：

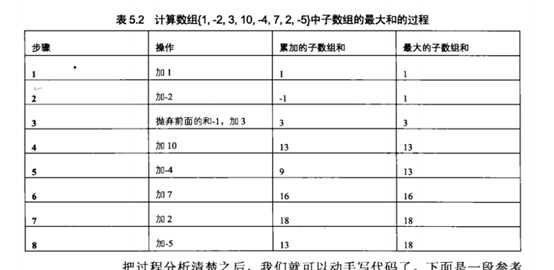
我们试着从头到尾逐个累加示例数组中的每个数字。初始化为0。第一步加上第一个数字1，此时和为1.接下来第二步加上数字-2，和就变成了-1，第三步加上数字3.我们注意到由于此前累计的和是-1，小于0，那如果用-1加上3，得到的和是2，比3本身还雄安。也就是说从第一个数字开始的子数组的和会小于从第三个数字开始的子数组的和。因此我们不用考虑第一个数字开始的子数组，之前累计的和也被抛弃。

 

 

 

 

从1到n整数中1出现的次数

题目：输入一个整数n，求从1到n这n个整数的十进制表示中1出现的次数。例如输入12，从1到12这些整数中包含1的数字有1，10，11和12，1一共出现了5次。

解题思路：

从数字规律着手明显提高时间效率的解法，能让面试官耳目一新

我们把从1到21345的所有数字分为两段，一段是从1到1345，另一段是从1346到21345.

我们先看从1346到21345中1出现的次数。1的出现分为两种情况。首先分析1出现在最高为的情况。从1346到21345的数字中，1出现在10000—19999这10000个数字的万位中，一共出现了10000个。

值得注意的是，并不是对所有的5位数而言在万位出现的次数都是10000个。对于万位是1的数字比如输入12345，1只出现在10000-12345的万位，出现的次数不是10000次，而是2346次，也就是除去最高数字之后剩下的数字再加上1（即2345+1=2346次）。

接下来分析1出现再除最高位之外的其他四位数中的情况。例子中1346-21345这20000个数字中后4位中1出现的次数是2000次，由于最高为是2，我们可以再把1346-21345分成两段，1346-11345和11346-21345.每一段剩下的4位数字中，选择其中一位是1，其余三位可以再0-9这10个数字中任意选择，因此根据排列组合原则，总共出现的次数是2*1000=2000次。

至于从1到1345中1出现的次数，我们就可以用递归求得了。这也是我们为什么要把1-21345分成1-1345和1346-21345两段的原因。因为把21345的最高为去掉就变成1345，便于我们采用递归的思路。