基于剪枝的回溯法

Posted 2023-02-02 用七年单身换个PolyU.CSPhD

主要内容

好久没上Leetcode，发现首页居然有一道中等题"全排列II"错了好多次一直没对，发现是带剪枝的回溯类型，做完了就稍微记录一下。

今天主要通过两个例题，一是回顾回溯法，二就是学会回溯的同时剪枝。

简单的全排列

力扣中的Q46，原题如下：

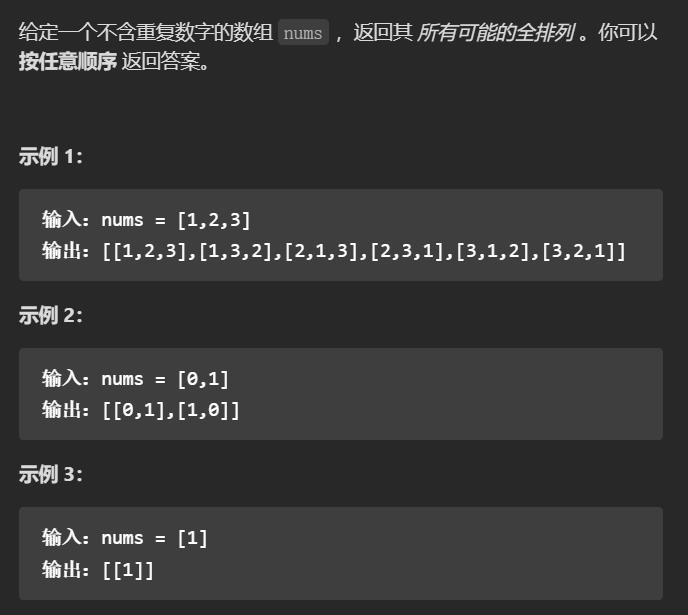
题目的温馨提示也很体贴地告诉了你数组中的各元素不相等，所以轮不到剪枝的技巧派上用场。

直接贴出代码：

class Solution 
public:
    vector<vector<int>> ans;
    vector<int> temp;
    void backtrack(vector<int>& nums, vector<bool>& traverse)
        if(temp.size() == nums.size())
            ans.push_back(temp);
            return;
        
        for(int i = 0 ; i < nums.size() ; i ++)
            if(!traverse[i])
                temp.push_back(nums[i]);
                traverse[i] =  true;
                backtrack(nums, traverse);
                traverse[i] = false;
                temp.pop_back();
            
        
    
    vector<vector<int>> permute(vector<int>& nums) 
        vector<bool> traverse(nums.size(), false);
        backtrack(nums, traverse);
        return ans;
    
;

类里temp是装一种排列的数组，ans则是全排列所有答案的二维数组。
主要是要熟练backtrack的操作：
回溯总是需要有一个"回去"的条件，也就是终止递归的条件，否则就是无穷无尽的递归直到"爆栈"。此处我们设置的终止条件就是temp装满了一次排列，也就是size和原数组相等时就找到一次排列了。
而对于如何寻找排列主要还是看循环里干了啥事。traverse是我们的一个访问数组，对应于下标而不是元素本身，没访问前所有下标都是false的。nums数组是题目给出的，希望我们找到所有排列的数组。
如果某个元素没被访问过就可以装入temp，且修改标记。当此元素后面的所有位置完成全排列后就会回退到这个元素，此时我们将其从当前位置弹出并修改访问位即可。
按照上述步骤就可以得到简单全排列。

需要剪枝的全排列

需要剪枝的最大原因就是数组中出现重复数字了。

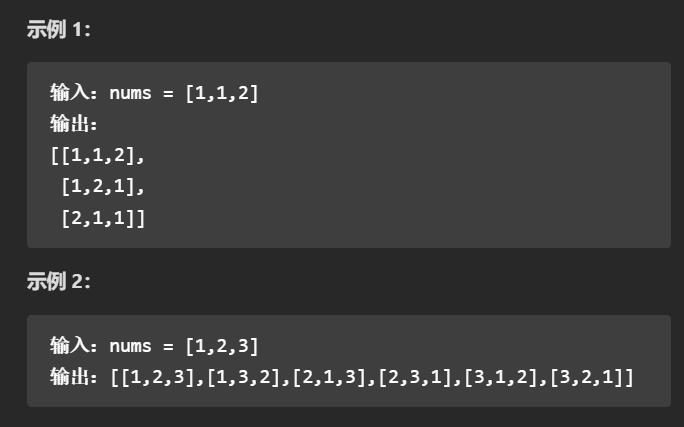
如果不带剪枝，那么每次判定到终止条件时我们还需要嵌套一层循环去判定这个temp是否已经在ans里出现过，没出现过才加入此种排列方式。
这样的效率极其低下，因此要学会如何在递归过程中剪枝而不是在递归结果处判定。

朴素回溯的逻辑在于，比如有例一数组[1, 1, 2]:
则将下标为0的元素置首，剩下的全排列
再将下标为1的元素置首，剩下的全排列
最后下标为2的元素置首，剩下的全排列

对于一个位置loc，假设现在企图把nums数组中下标为index的数字填到loc处，那么index之前的那些数字都已经被尝试过填到loc处。
显然，如果当前index这个数字与index - 1下标处的数字相同的话，整个排列就重复了！所以假如相同这个情况，loc处就不需要再填index下标的数字了，换下一个！
代码如下：

class Solution 
public:
    vector<vector<int>> ans;
    vector<int> vec;

    void dfs(vector<bool>& visited, vector<int>& nums)
        if(vec.size() == nums.size())
            ans.push_back(vec);
            return;
        
        for(int i = 0 ; i < nums.size() ; i ++)
            if(i - 1 >= 0 && !visited[i - 1] && nums[i] == nums[i - 1])
                continue;
            if(!visited[i])
                visited[i] = true;
                vec.push_back(nums[i]);
                dfs(visited, nums);
                vec.pop_back();
                visited[i] = false;
            
        
    

    vector<vector<int>> permuteUnique(vector<int>& nums) 
        sort(nums.begin(), nums.end(), [](int item1, int item2)
            return item1 > item2;
        );
        int sz = nums.size();
        vector<bool> visited(sz, false);
        dfs(visited, nums);
        return ans;
    
;

还有一个关键点就是nums数组得事先排序。