解数独算法的实现——剪枝优化
Posted 爱吃土豆的男孩
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了解数独算法的实现——剪枝优化相关的知识,希望对你有一定的参考价值。
最近人工智能做个小实验,组队选了个数独游戏,顺便研究了一下。解数独感觉主流思想也就是深搜回溯了吧,优化就是各种剪枝方法。
1 引言
数独起源于18世纪初瑞士数学家欧拉等人研究的拉丁方阵(Latin Square),曾风靡日本和英国。现有解法包括基础解法:摒除法,余数法,进阶解法:区块摒除法(Locked Candidates)、数组法(Subset)、四角对角线(X-Wing)、唯一矩形(Unique Rectangle)、全双值坟墓(Bivalue Universal Grave)、单数链(X-Chain)、异数链(XY-Chain)及其他数链的高级技巧等等。已发展出来的方法有近百种之多。本解法中使用了余数法和数组法。
2 算法原理
用个9*9的vector保存整个游戏,注意的是这里的9*9不是9行9列,而是9个九宫格,起初考虑时是希望能更简洁,不过最终都会用到位置所在的行数,列数和所在九宫格,似乎存行列只需要通过行列求9宫格更方便,而存9*九宫格要通过第几个九宫格和九宫格中第几个位置来求行列,更复杂(—_—)! 算是个坑,以后有同学在做的话,要注意了哦!
算法的流程也很简单,上个流程图,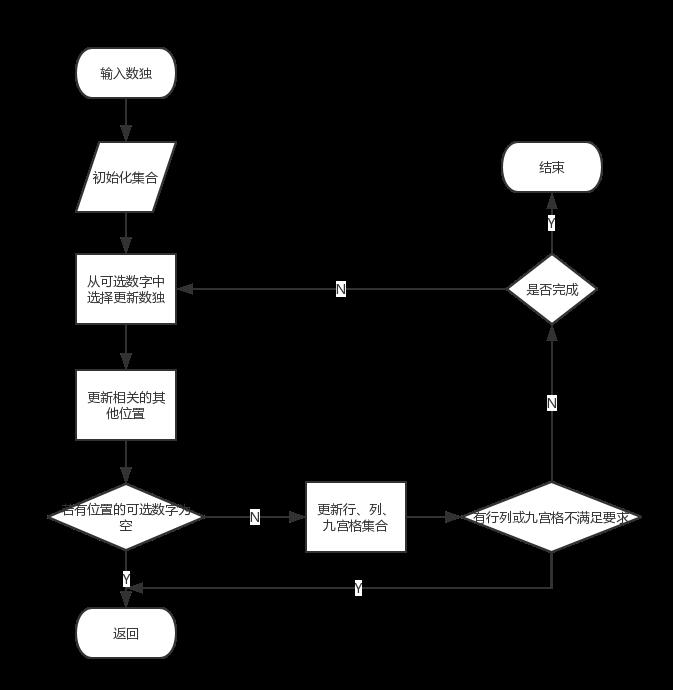
首先,数据结构是9*9的游戏盘,然后为每个位置的可选数字维护一个集合(set),每次更新数字时会同时更新相关位置的集合,稍后会讲到。还有个3*9的集合,是每行每列每个九宫格的可选数字的集合。
然后说说剪枝算法,前面说到用了余数法和数组法,要声明的一点是,这些解法都是人类的解法,即为人类如何选取数字而达到最快解出题目,不过我们计算机深搜是直接选取可选数字最少的位置,所以可能叫法有争议,在此就不深入讨论了。
(1)余数法
每次选择数字后,都要删除对应位置的可选数,及同行同列同九宫格中不能再次选择相同的数字了,所以更新下面图片中灰色位置的集合,如果有位置的可选数字为空,则回溯。
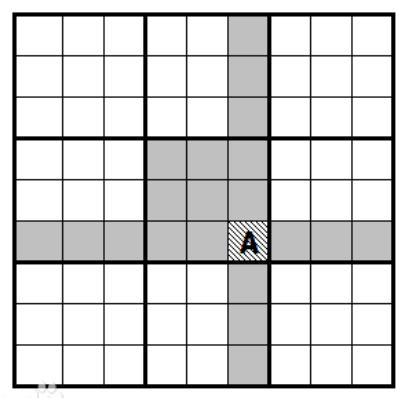
(2)数组法
或许有的时候更新后所有位置都有可选数字,但此时已经出现冲突,例如,一行中只有2个空位,而他们的可选数字相同,这时一定无解了,所以需要回溯。
为了检测,我们需要将更新过的位置所处的行列九宫格的集合全部更新,(灰色位置包括的行列九宫格,实际就是所有行列和5个九宫格),更新方法就是对该集合包含的所有位置的可选数+已选数求并集,得出集合大小小于9则产生了冲突,回溯。
3 代码
1 #include <iostream> 2 #include <vector> 3 #include <set> 4 #include <cstdlib> 5 #include <ctime> 6 #include <fstream> 7 8 using namespace std; 9 10 11 class Sudoku{ 12 public: 13 vector<vector<int> > numMap;//9*9 0 14 vector<vector<set<int> > > availableNum;//row,col,nine 1~9 15 vector<vector<set<int> > > everyNum; 16 17 Sudoku(vector<vector<int> > v){ 18 initMap(v); 19 } 20 21 bool updateMap(int small,int big,int value){ //9*9 vector everyNum[big][small] = value 22 if(numMap[big][small]==0){ //更新游戏盘,删除相关位置中的value 23 set<int> &row = availableNum[0][getRow(small,big)]; 24 set<int> &col = availableNum[1][getCol(small,big)]; 25 set<int> &nin = availableNum[2][big]; 26 set<int>::iterator rowIt = row.find(value); 27 set<int>::iterator colIt = col.find(value); 28 set<int>::iterator ninIt = nin.find(value); 29 if(rowIt!=row.end()&& 30 colIt!=col.end()&& 31 ninIt!=nin.end()){ 32 row.erase(rowIt); 33 col.erase(colIt); 34 nin.erase(ninIt); 35 numMap[big][small] = value; 36 set<int> s; 37 everyNum[big][small] =s; //选中后集合中只有一个选中的数字本身 38 everyNum[big][small].insert(value); 39 if(updateEve(small,big,value)) 40 return true; 41 } 42 } 43 return false; 44 } 45 bool updateEve(int small,int big,int value){ 46 for(int i=0;i!=9;++i){ 47 if(numMap[big][i]==0){ 48 set<int>::iterator it = everyNum[big][i].find(value); 49 if(it!=everyNum[big][i].end()){ 50 everyNum[big][i].erase(it); 51 } 52 if(everyNum[big][i].size()==0) 53 return false; 54 } 55 } 56 int r = getRow(small,big); 57 for(int j=0;j!=3;++j){ 58 for(int k=0;k!=3;++k){ 59 int a=r/3*3+j; 60 int b=r%3*3+k; 61 if(numMap[a][b]==0){ 62 set<int>::iterator it = everyNum[a][b].find(value); 63 if(it!=everyNum[a][b].end()){ 64 everyNum[a][b].erase(it); 65 } 66 if(everyNum[a][b].size()==0) 67 return false; 68 69 } 70 } 71 for(int j=0;j!=3;++j){ 72 for(int k=0;k!=3;++k){ 73 int a=big%3+j*3; 74 int b=small%3+k*3; 75 if(numMap[a][b]==0){ 76 set<int>::iterator it = everyNum[a][b].find(value); 77 if(it!=everyNum[a][b].end()){ 78 everyNum[a][b].erase(it); 79 } 80 if(everyNum[a][b].size()==0) 81 return false; 82 83 } 84 } 85 return true; 86 } 87 bool check(){ //数组法检查 88 for(int i=0;i!=9;++i){ 89 set<int> s; 90 for(int j=0;j!=9;++j){ 91 for(auto it:everyNum[i][j]){ 92 s.insert(it); 93 } 94 } 95 if(s.size()!=9) 96 return false; 97 } 98 for(int r=0;r!=9;++r){ 99 set<int> s; 100 for(int j=0;j!=3;++j){ 101 for(int k=0;k!=3;++k){ 102 int a=r/3*3+j; 103 int b=r%3*3+k; 104 for(auto it:everyNum[a][b]){ 105 s.insert(it); 106 } 107 } 108 } 109 if(s.size()!=9) 110 return false; 111 } 112 for(int c=0;c!=9;++c){ 113 set<int> s; 114 for(int j=0;j!=3;++j){ 115 for(int k=0;k!=3;++k){ 116 int a=j*3+c/3; 117 int b=k*3+c%3; 118 for(auto it:everyNum[a][b]){ 119 s.insert(it); 120 } 121 } 122 } 123 if(s.size()!=9) 124 return false; 125 } 126 return true; 127 } 128 void initMap(vector<vector<int> > vv){ 129 vector<int> v(9,0); 130 set<int> s; 131 for(int i=1;i!=10;++i){ 132 s.insert(i); 133 } 134 vector<set<int> > sv(9,s); 135 availableNum = vector<vector<set<int> > >(3,sv); 136 everyNum = vector<vector<set<int> > >(9,sv); 137 numMap = vector<vector<int> >(9,v); 138 for(int i=0;i!=9;++i){ 139 vector<int> tmp = vv[i]; 140 for(int j=0;j!=3;++j){ 141 for(int k=0;k!=3;++k){ 142 numMap[i/3*3+j][i%3*3+k]=tmp[j*3+k]; 143 if(tmp[j*3+k]!=0){ 144 int value = tmp[j*3+k]; 145 set<int> a; 146 everyNum[i/3*3+j][i%3*3+k] = a; 147 set<int> &row = availableNum[0][getRow(i%3*3+k,i/3*3+j)]; 148 set<int> &col = availableNum[1][getCol(i%3*3+k,i/3*3+j)]; 149 set<int> &nin = availableNum[2][i/3*3+j]; 150 set<int>::iterator rowIt = row.find(value); 151 set<int>::iterator colIt = col.find(value); 152 set<int>::iterator ninIt = nin.find(value); 153 row.erase(rowIt); 154 col.erase(colIt); 155 nin.erase(ninIt); 156 } 157 } 158 } 159 } 160 showMap(); 161 set<int> tmp; 162 for(int i=0;i!=9;++i){ 163 for(int j=0;j!=9;++j){ 164 if(numMap[i][j]==0){ 165 everyNum[i][j] = getEve(j,i); 166 } 167 else{ 168 everyNum[i][j] = tmp; 169 everyNum[i][j].insert(numMap[i][j]); 170 } 171 172 } 173 } 174 showEve(); 175 } 176 set<int> getEve(int small,int big){ 177 set<int> &row = availableNum[0][getRow(small,big)]; 178 set<int> &col = availableNum[1][getCol(small,big)]; 179 set<int> &nin = availableNum[2][big]; 180 set<int> res; 181 for(auto it:row){ 182 if(col.find(it)!=col.end()&&nin.find(it)!=nin.end()){ 183 res.insert(it); 184 } 185 } 186 return res; 187 } 188 189 pair<int,int> getMin(){ 190 pair<int,int> res = make_pair(9,9); 191 int Min =10; 192 for(int i=0;i!=9;++i){ 193 for(int j=0;j!=9;++j){ 194 if(numMap[i][j]==0&&everyNum[i][j].size()<Min){ 195 res = make_pair(i,j); 196 Min = everyNum[i][j].size(); 197 } 198 } 199 } 200 return res; 201 } 202 int getEveNum(int small,int big){ 203 set<int> &row = availableNum[0][getRow(small,big)]; 204 set<int> &col = availableNum[1][getCol(small,big)]; 205 set<int> &nin = availableNum[2][big]; 206 int res=0; 207 for(auto it:row){ 208 if(col.find(it)!=col.end()&&nin.find(it)!=nin.end()){ 209 res++; 210 } 211 } 212 return res; 213 } 214 int getRow(int small,int big){ 215 return big/3*3+small/3; 216 } 217 int getCol(int small,int big){ 218 return big%3*3+small%3; 219 } 220 void showMap(){ 221 for(int i=0;i!=9;++i){ 222 cout<<" "; 223 if(i%3==0){ 224 cout<<"---------------------"<<endl; 225 cout<<" "; 226 } 227 for(int j=0;j!=3;++j){ 228 cout<<"|"; 229 for(int k=0;k!=3;++k){ 230 if(numMap[i/3*3+j][i%3*3+k]==0) 231 cout<<" "; 232 else 233 cout<<numMap[i/3*3+j][i%3*3+k]<<" "; 234 } 235 } 236 cout<<"|"<<endl; 237 } 238 cout<<" "; 239 cout<<"---------------------"<<endl; 240 241 } 242 void showEve(){ 243 for(int i=0;i!=9;++i){ 244 cout<<" "; 245 if(i%3==0){ 246 cout<<"---------------------"<<endl; 247 cout<<" "; 248 } 249 for(int j=0;j!=3;++j){ 250 cout<<"|"; 251 for(int k=0;k!=3;++k){ 252 if(numMap[i/3*3+j][i%3*3+k]==0){ 253 for(auto it:everyNum[i/3*3+j][i%3*3+k]) 254 cout<<it; 255 cout<<" "; 256 } 257 else 258 cout<<numMap[i/3*3+j][i%3*3+k]<<" "; 259 } 260 } 261 cout<<"|"<<endl; 262 } 263 cout<<" "; 264 cout<<"---------------------"<<endl; 265 266 } 267 }; 268 269 bool solu(Sudoku mSudoku,int small,int big,int value); 270 bool solu(Sudoku mSudoku); 271 bool solu1(Sudoku mSudoku,int small,int big,int value); 272 bool solu1(Sudoku mSudoku){ 273 pair<int,int> p = mSudoku.getMin(); 274 for(auto i:mSudoku.everyNum[p.first][p.second]){ 275 if(solu1(mSudoku,p.second,p.first,i)) 276 return true; 277 } 278 return false; 279 } 280 bool solu(Sudoku mSudoku){ 281 pair<int,int> p = mSudoku.getMin(); 282 for(auto i:mSudoku.everyNum[p.first][p.second]){ 283 if(solu(mSudoku,p.second,p.first,i)) 284 return true; 285 } 286 return false; 287 } 288 289 bool solu(Sudoku mSudoku,int small,int big,int value){ 290 if(!mSudoku.updateMap(small,big,value)) 291 return false; 292 pair<int,int> p = mSudoku.getMin(); 293 if(p==make_pair(9,9)){ 294 mSudoku.showMap(); 295 return true; 296 } 297 for(auto i:mSudoku.everyNum[p.first][p.second]){ 298 if(solu(mSudoku,p.second,p.first,i)) 299 return true; 300 } 301 return false; 302 } 303 304 bool solu1(Sudoku mSudoku,int small,int big,int value){ 305 if(!mSudoku.updateMap(small,big,value)||!mSudoku.check()) 306 return false; 307 p以上是关于解数独算法的实现——剪枝优化的主要内容,如果未能解决你的问题,请参考以下文章