数据结构 图的基本操作要C语言的完整代码！！

Posted

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了数据结构 图的基本操作要C语言的完整代码！！相关的知识，希望对你有一定的参考价值。

（1）键盘输入数据，建立一个有向(无向）网的邻接矩阵（或邻接表）。
（2）输出该邻接矩阵。
（3）在邻接矩阵（或邻接表）的基础上计算各顶点的度，并输出。
（4）采用邻接矩阵（或邻接表）存储实现无向图的深度优先遍历。
（5）采用邻接矩阵（或邻接表）存储实现无向图的广度优先遍历。
（6）采用邻接矩阵存储实现无向图的最小生成树的PRIM算法。
（7）采用邻接矩阵存储一个有向图，输出单源点到其它顶点的最短路径。
（8）在主函数中设计一个简单的菜单，分别调试上述算法。
有答案加分！！

参考技术A #include<stdio.h>
#define n 6
#define e 8
void CREATGRAPH();

typedef char vextype;
typedef float adjtype;
typedef struct
vextype vexs[n];
adjtype arcs[n][n];

graph;
int main()


CREATGRAPH();
printf("创建成功！\n");


void CREATGRAPH()

graph *ga;
int i,j,k;
float w;
for(i=0;i<n;i++)
ga->vexs[i]=getchar();
for(i=0;i<n;i++)
for(j=0;j<n;j++)
ga->arcs[i][j]=0;
for(k=0;k<e;k++)

scanf("%d%d%f",&i,&j,&w);
ga->arcs[i][j]=w;
ga->arcs[j][i]=w;


printf("创建成功！\n");


没写完，，自己加加吧！ 参考技术B 一分都么得....

邻接矩阵和邻接表存储的图的基本操作及完整代码

文章目录

本文中实现代码只出给关键算法，完整代码请移步我的资源中免费下载。

邻接矩阵存储的图

图的邻接矩阵存储结构定义：

#define maxVertexNum 30 //图中顶点数目的最大值
typedef char VertexType;  //图中顶点的数据类型
typedef int EdgeType;  //边上权值的数据类型
typedef struct{
    VertexType Vertex[maxVertexNum]; //顶点表
    EdgeType Edge[maxVertexNum][maxVertexNum];  //邻接矩阵，边表
    int vexnum,edgenum; //图的顶点数和边数
}MGraph;

构建带权图的邻接矩阵表示

题目描述：
设有一个带权图G，设计一个算法，输入n个顶点数据和e条边的顶点号i、j及其权值w，构建它的邻接矩阵表示。

实现代码：

//顶点值转换为位置（数组下标）
int getPos(MGraph G, VertexType v){
    int i;
    for(i=0; i<G.vexnum; i++){
        if(G.Vertex[i] == v){
            break;
        }
    }
    return i;
}

void BuildMGraph(MGraph &G, VertexType v[], int n, VertexType edge[][2], EdgeType w[], int e, int d){
    //顶点数据放在v[n]中，边的两个顶点放在edge[e][2]中，边上的权值放在w[e]中
    //对于第i个顶点，edge[i][0]和edge[i][1]分别是顶点数据，c[i]是其权值
    //规定若d=1形成有向图，d=0形成无向图
    G.vexnum = n;
    G.edgenum = e;
    for(int i=0; i<G.vexnum; i++){ //初始化
        G.Vertex[i] = v[i]; //顶点表
        for(int j=0; j<G.vexnum; j++){
            G.Edge[i][j] = (i==j)? 0 : maxweight; //边表
        }
    }
    //建立邻接矩阵
    for(int k=0; k<G.edgenum; k++){
        int i = getPos(G, edge[k][0]);
        int j = getPos(G, edge[k][1]);
        G.Edge[i][j] = w[k]; //边赋值
        if(d==0) G.Edge[j][i] = w[k]; //无向图则对称
    }
}

运行结果：
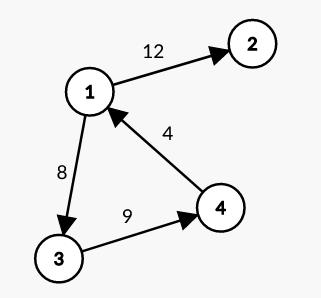
第一行输入：结点数n 边数e 有向图还是无向图d
接下来n行：输入顶点值
接下来e行：输入边的顶点及对应权值
最后输出该图对应的邻接矩阵


第一个邻接顶点FirstNeighbor

这里的图是以1，2，3，……为顶点的图。以下相同，不再赘述。
题目描述：
设带权图的邻接矩阵表示为G，设计算法实现取图中顶点v的第一个邻接顶点的运算FirstNeighobor（G，v）。

实现代码：

int FirstNeighbor(MGrpah G, int v){
    if(v != -1){
        for(int i=0; i<G.vexnum; i++){
            if(G.Edge[v][i]>0 && G.Edge[v][i]<maxweight){ //第v行第一个存在权值的顶点号
                return i;
            }
        }
    }
    return -1; //v的邻接顶点不存在
}

下一个邻接点NextNeighbor

题目描述：
设带权图的邻接矩阵表示为G，设计算法实现取图中顶点v的邻接顶点w的下一个邻接顶点NextNeighobor（G，v，w）。

实现代码：

int NextNeighbor(MGrpah G, int v, int w){
    if(v!=-1 && w!=-1){
        for(int i=w+1; i<G.vexnum; i++){  //第v行第一个邻接点w的下一个邻接点
            if(G.Edge[v][i]>0 && G.Edge[v][i]<maxweight){ 
                return i;
            }
        }
    }
    return -1; //不存在
}

邻接表存储的图

图的邻接表存储表示结构定义：

#define maxVertexNum 30  //最大顶点数
typedef char VertexType;  //顶点的数据类型
typedef int EdgeType;  //边上权值的数据类型
#define maxweight 0x3f3f3f3f  //最大权值

typedef struct ENode{  //边表结点
    int adjvex; //邻接点域
    struct ENode *nextarc; //指针域
    EdgeType weight; //边上的权值
}EdgeNode;
typedef struct VNode{  //顶点表结点
    VertexType data; //顶点域
    struct ENode *firstarc;  //边表头指针
}VertexNode;
typedef struct{
    VertexNode VertexList[maxVertexNum]; //顶点表
    int vexnum, edgenum; //顶点数和边数
}ALGraph;

构建带权图的邻接表存储表示

问题描述：
设有一个带权图G，设计一个算法，输入n个顶点数据和e条边的端顶点号 i、j及其权值w，构建它的邻接表存储表示。

实现代码：

//查询顶点在图中的存储地址（数组下标）
int getPos(ALGraph G, VertexType x){
    int i;
    for(i=0; i<G.vexnum; i++){
        if(G.VertexList[i].data == x){
            break;
        }
    }
    return i;
}

void CreateALGraph(ALGraph &G, VertexType v[], int n, VertexType edge[][2], EdgeType w[], int e, int d){
    //顶点数据放在v[n]中，边的顶点对放在edge[e][2]中，权值放在w[e]中
    //对于第i个顶点，edge[i][0]和edge[i][1]分别是顶点数据，w[i]是其对应权值
    //d=0建立带权无向图，d=1建立带权有向图
    G.vexnum = n;
    G.edgenum = e;
    for(int i=0; i<G.vexnum; i++){ //建立顶点表
        G.VertexList[i].data = v[i];
        G.VertexList[i].firstarc = NULL;
    }
    for(int i=0; i<G.edgenum; i++){ //建立边表
        VertexType e1 = edge[i][0];
        VertexType e2 = edge[i][1]; //边的顶点对
        int j = getPos(G, e1);
        int k = getPos(G, e2); //存储位置
        EdgeNode *p, *q;
        p = G.VertexList[j].firstarc; //边链表头指针
        while(p!=NULL && p->adjvex != k) //从边链表头开始遍历，看是否有重边
            p = p->nextarc;
        if(p == NULL){  //图中没有重边，加入新边
            q = (EdgeNode *)malloc(sizeof(EdgeNode));
            q->adjvex = k;  //邻接点为e2
            q->weight = w[i];  //e1、e2的权值为w[i]
            q->nextarc = G.VertexList[j].firstarc;  //前插链入顶点j的边链表
            G.VertexList[j].firstarc = q;
            if(d == 0){ //无向图
                q = (EdgeNode *)malloc(sizeof(EdgeNode));
                q->adjvex = j;
                q->weight = w[i];
                q->nextarc = G.VertexList[k].firstarc; //前插链入顶点k的边链表
                G.VertexList[k].firstarc = q;
            }
        }
        else{ //有重边，则更新权值
            p->weight = w[i];
        }
    }
}

运行结果：
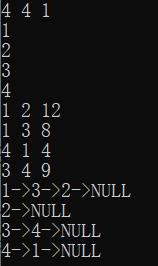
第一行输入：结点数n 边数e 有向图还是无向图d
接下来n行：输入顶点值
接下来e行：输入边的顶点及对应权值
最后输出该图对应的邻接表


第一个邻接顶点FirstNeighbor

题目描述：
设带权图的邻接表表示为G，设计算法实现取图中顶点v的第一个邻接顶点的运算FirstNeighobor（G，v）。

实现代码：

int FirstNeighbor(ALGraph G, int v){
    if(v != -1){
        EdgeNode *p = G.VertexList[v].firstarc; //对应边链表的第一个结点
        if(p!=NULL){
            return p->adjvex;
        }
    }
    return -1; //第一个邻接顶点不存在
}

下一个邻接点NextNeighbor

题目描述：
设带权图的邻接表表示为G，设计算法实现取图中顶点v的邻接顶点w的下一个邻接顶点NextNeighobor（G，v，w）。

实现代码：

int NextNeighbor(ALGraph G, int v, int w){
    if(v!=-1 && w!=-1){
        EdgeNode *p = G.VertexList[v].firstarc; //对应边链表的第一个结点
        while(p!=NULL && p->adjvex!=w) p=p->nextarc; //找到v的邻接点w
        if(p!=NULL && p->nextarc!=NULL) //w存在且w的邻接点存在
            return p->nextarc->adjvex;
    }
    return -1; //下一个邻接点不存在
}

以上是关于数据结构 图的基本操作要C语言的完整代码！！的主要内容，如果未能解决你的问题，请参考以下文章

邻接矩阵和邻接表存储的图的基本操作及完整代码

基于FFT的算法优化 要C语言完整程序（利用旋转因子的性质），有的请留言，答谢！！！(有核心代码，望指教

图的存储代码实现

图的基本概念以及特殊形态的图（C语言）

图的深度/广度优先遍历C语言程序

数据结构(C语言版)严蔚敏---图的操作的相关代码