SVM&范数&SVD
Posted oliveQ
tags:
篇首语:本文由小常识网(cha138.com)小编为大家整理,主要介绍了SVM&范数&SVD相关的知识,希望对你有一定的参考价值。
SVM&范数&SVD
支持向量机SVM
线性判别
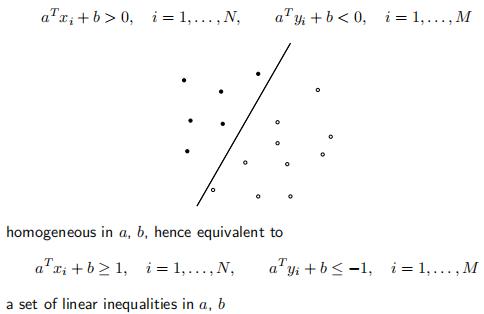
最大分类间隔器
利用线性判别的性质,可以通过最大间隔来做分类【直线是超平面,两侧直线上的点是支持向量】
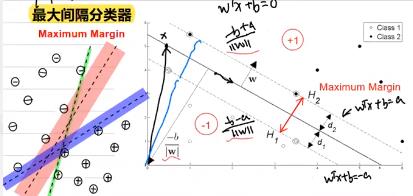
两平面间的距离计算公式

于是距离宽度是
d
i
s
t
=
2
a
∣
∣
w
∣
∣
2
∝
1
∣
∣
w
∣
∣
2
dist=\\frac2a||w||_2\\propto \\frac1||w||_2
dist=∣∣w∣∣22a∝∣∣w∣∣21
所以不妨令
a
=
1
a=1
a=1
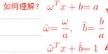
-
目标函数: max 1 ∣ ∣ w ∣ ∣ 2 ⟺ min ∣ ∣ w ∣ ∣ 2 2 2 \\max\\frac1||w||_2\\iff\\min\\frac||w||_2^22 max∣∣w∣∣21⟺min2∣∣w∣∣22
-
约束条件: f ( x ) = 1 − y i ( w T x i + b ) f(x)=1-y_i(w^Tx_i+b) f(x)=1−yi(wTxi+b),标签y=1/-1
-
目的是寻找超平面的参数 w ^ 和 b ^ \\hatw和\\hatb w^和b^
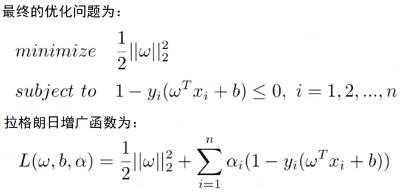
对偶函数: g ( α ) = inf w , b L ( w , b , α ) g(\\alpha)=\\inf_w,bL(w,b,\\alpha) g(α)=infw,bL(w,b,α) -
KKT的四个条件
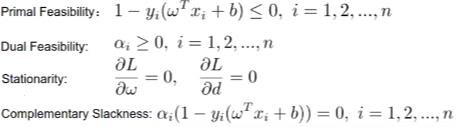
-
求导计算

得到 g ( α ) = − 1 / 2 ∑ i ∑ j α i α j y i y j x i x j + ∑ i = 1 n α i g(\\alpha)=-1/2\\sum_i\\sum_j\\alpha_i\\alpha_jy_iy_jx_ix_j+\\sum_i=1^n\\alpha_i g(α)=−1/2∑i∑jαiαjyiyjxixj+∑i=1nαi -
设 H i j = y i y j x i ∗ x j ∈ S + + n H_ij=y_iy_jx_i*x_j\\isin S_++^n Hij=yiyjxi∗xj∈S++n对称半正定矩阵
于是 g ( α ) = − 1 / 2 α T H α + 1 T α g(\\alpha)=-1/2\\alpha^TH\\alpha+1^T\\alpha g(α)=−1/2αTHα+1Tα -
转变求对偶问题
max − 1 / 2 α T H α + 1 T α \\max-1/2\\alpha^TH\\alpha+1^T\\alpha max−1/2αTHα+1Tα
s . t . α ≥ 0 , ∑ α i y i = 0 s.t.\\space \\alpha\\geq0,\\sum\\alpha_iy_i=0 s.t. α≥0,∑αiyi=0 -
用QP-solver得到 α , w ^ = ∑ i ∈ S α i y i x i , α i ≠ 0 \\alpha,\\hatw=\\sum_i\\isin S\\alpha_iy_ix_i,\\alpha_i\\neq0 α,w^=∑i∈Sαiyixi,αi=0
-
b ^ = 1 / N S ∑ i ∈ S ( y i − ∑ j α j y j x j ∗ x i ) \\hatb=1/N_S \\sum_i\\isin S(y_i-\\sum_j\\alpha_jy_jx_j*x_i) b^=1/NS∑i∈S(yi−∑jαjyjxj∗xi)
-
y i = ∑ j ∈ S α j y j x j ∗ x i + b ^ y_i=\\sum_j\\isin S\\alpha_jy_jx_j*x_i+\\hatb yi=∑j∈Sαjyjx以上是关于SVM&范数&SVD的主要内容,如果未能解决你的问题,请参考以下文章