二叉搜索树BST

Posted 2020-11-19 mini-coconut

二叉搜索树，也称有序二叉树,排序二叉树，是指一棵空树或者具有下列性质的二叉树：

1. 若任意节点的左子树不空，则左子树上所有结点的值均小于它的根结点的值；

2. 若任意节点的右子树不空，则右子树上所有结点的值均大于它的根结点的值；

3. 任意节点的左、右子树也分别为二叉查找树。

4. 没有键值相等的节点。

通过中序遍历可以得到一个有序数列。一个无序序列可以通过构造一棵二叉排序树变成一个有序序列，构造树的过程即为对无序序列进行排序的过程。每次插入的新的结点都是二叉排序树上新的叶子结点，在进行插入操作时，不必移动其它结点，只需改动某个结点的指针，由空变为非空即可。搜索,插入,删除的复杂度等于树高，O(log(n)).

（1）BST的建立

首先需要建立一个节点Node的结构体，这个结构体表示每个Node节点包括数值，左孩子，右孩子。当然一般还加上一个构造函数用于后面的初始化。

struct Node
{
    int val;
    Node* left;
    Node* right;
    Node( const int& value)  :left(NULL)  ,right(NULL)  ,val(value)  {}  
};

另外我们就要像新建一个链表一样来完成一个二叉搜索树的创建。这里采用的是每输入一个值，以-1作为结束，就调用插入函数Insert（这个函数自己定义实现，后面会说），Insert函数会将这个节点连接到它该在的位置。Insert函数需要的参数是root根节点和插入的值value的值。注意这里root根节点要用引用传递，否则我每次调用完函数，root节点不变。

Node* creatBST()
{
    Node *root;
    root=NULL;
    int a;
    cin>>a;
    while(a!=-1)
    {
        Insert(root,a);
         cin>>a;
    }
    return root;
}

（2）BST的输出

我们利用BST的性质，因为BST的中序遍历就是一个有序的数列，所以我们输出用中序遍历来检测我们的程序结果。

void _InOrder(const Node* root)  
{
    if (root == NULL)
    　　return;  
  _InOrder(root->left);  
  cout << root->val << " ";
  _InOrder(root->right);  
}

这里采用的是递归形式的中序遍历。非递归形式，需要大家去学习，我前面有总结过。

（3）BST的插入

插入的操作很简单，有递归和非递归（迭代）两种实现方法。我们首先总结BST插入的迭代实现方法。

首先我们要明白，BST的插入永远是插入到叶子节点的后面，所以不会出现插入到中间的情况，我们只需要去比较每个节点的值和当前需要插入的值的大小，就能找到正确的插入位置。这里用两个Node型的指针，cur指向当前位置，parent指向当前位置的父节点。cur负责找到要插入的位置，parent负责插入的实现。

bool Insert(Node* &root,const int& value)  
{  
    if (root == NULL)
    {  
        root = new Node(value);  
    }  
    Node* cur=root;  
    Node* parent = NULL;  
    //首先找到要插入的位置  
    while (cur)  
    {  
        if (cur->val > value)  
        {  
            parent = cur;  
            cur = cur->left;  
        }  
        else if(cur->val<value)  
        {  
            parent = cur;  
            cur = cur->right;  
        }  
        else  
        {  
            return false;  
        }  
    }  
    //在找到插入位置以后，判断插入父亲节点的左边还是右边  
    if (parent->val > value)  
    {  
        parent->left = new Node(value);  
    }  
    else  
    {  
        parent->right = new Node(value);  
    }  
    return true;  
}

递归形式也很简单

bool Insert(Node*& root, const int& value)  
{  
    if (root == NULL)  
    {  
        root = new Node(value);  
        return true;  
    }  
    if (root->val > value)  
    {  
        return Insert(root->left, value);  
    }  
    else if(root->val < value)  
    {  
        return Insert(root->right,value);  
    }  
    else  
    {  
        return false;  
    }  
}  

（3）BST的删除操作

BST的删除是最复杂的，之所以复杂，是因为要分几种情况。所以我们只要弄清楚删除一个节点的逻辑，程序的实现自然不难。

二叉搜索树的删除：

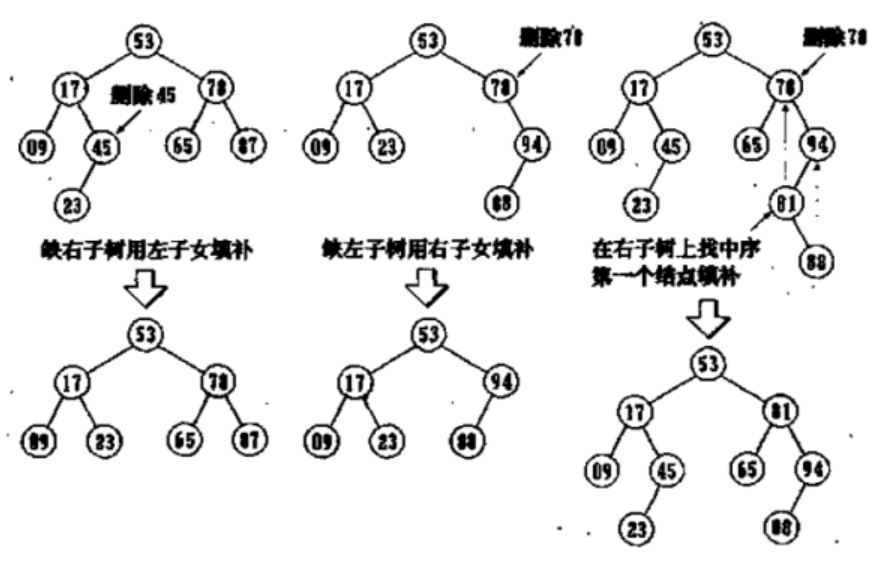
主要分三大种情况，（1）如果要删除的节点只有左子树，那么就将该节点的父节点指向该节点的左子树，删除该节点就好了

（2）如果要删除的节点只有右子树，那么就将该节点的父节点指向该节点的右子树，删除该节点就好了

（3）如果要删除的节点左右子树都有，那么就要找比该节点的左节点要大一个数的节点，这个时候自然不能直接将右子树直接提上去，所以我们要找该节点右子树的最左孩子，也就是右子树中序遍历的第一个数。

bool Remove(Node* &root,const int& value)  
{  
    //没有节点  
    if (root == NULL)  
    {  
        return false;  
    }  
    //只有一个节点  
    if (root->left == NULL&&root->right == NULL)  
    {  
        if (root->val == value)  
        {  
            delete root;  
            root = NULL;  
            return true;  
        }  
        return false;  
    }  
  
    Node* parent = NULL;  
    Node* cur = root;  
    //遍历查找要删除节点的位置  
    while (cur)  
    {  
        Node* del = NULL;  
        if (cur->val > value)  
        {  
            parent = cur;  
            cur = cur->left;  
        }  
        else if (cur->val < value)  
        {  
            parent = cur;  
            cur = cur->right;  
        }  
        else  
        {  
            //要删除节点的左子树为空，分3种情况  
            if (cur->left == NULL)  
            {  
                //注意判断父节点是否为空，若为空，则要删除的节点为根节点
               /* if (parent == NULL)  
                {  
                    root = cur->right;  
                    delete cur;  
                    cur = NULL;  
                    return true;  
                }  */
                if (parent->val > cur->val)  
                {  
                    del = cur;  
                    parent->left = cur->right;  
                    delete del;  
                    return true;  
                }  
                else if (parent->val < value)  
                {  
                    del = cur;  
                    parent->right = cur->right;  
                    delete del;  
                    return true;  
                }  
            }  
            //要删除节点的右子树为空，同样分3种情况  
            else if (cur->right == NULL)  
            {  
                //注意判断父节点是否为空，若为空，则要删除的节点为根节点,如：只有根节点5和其左节点3  
             /*   if (parent == NULL)  
                {  
                    root = cur->left;  
                    delete cur;  
                    cur = NULL;  
                    return true;  
                }  */
                if (parent->val > cur->val)  
                {  
                    del = cur;  
                    parent->left = cur->left;  
                    delete del;  
                    return true;  
                }  
                else if (parent->val < cur->val)  
                {  
                    del = cur;  
                    parent->right = cur->left;  
                    delete del;  
                    return true;  
                }  
            }  
            //左右子树都不为空  
            else  
            {  
                Node* del = cur;  
                Node* parent = NULL;  
                Node* RightFirst = cur->right;  
                //右边第一个节点的左子树为空  
                if (RightFirst->left == NULL)  
                {  
                    swap(RightFirst->val, cur->val);  
                    del = RightFirst;
                    cur->right = RightFirst->right;  
                    delete del;  
                    return true;  
                }  
                //右边第一个节点的左子树不为空  
                while (RightFirst->left)  
                {  
                    parent = RightFirst;  
                    RightFirst = RightFirst->left;  
                }  
                   swap(RightFirst->val, cur->val);  
                   del = RightFirst;  
                   parent->left = RightFirst->right;  
                   delete del;  
                   return true;  
            }  
        }  
    }  
    return false;  
}  

递归形式也可以写

bool Remove(Node*& root, const int& value)  
{  
    //没有节点  
    if (root == NULL)  
    {  
        return false;  
    }  
    //只有一个节点  
    if (root->left == NULL&&root->right == NULL)  
    {  
        if (root->val == value)  
        {  
            delete root;  
            root = NULL;  
            return true;  
        }  
        else  
        {  
            return false;  
        }  
  
    }  
  
    //删除二叉搜索树节点的递归写法  
    if (root->val > value)  
    {  
        Remove(root->left, value);  
    }
    else if (root->val <value)  
    {  
        Remove(root->right, value);  
    }  
    else  
    {  
        Node* del = NULL;  
          
        if (root->left == NULL)  
        {  
            del = root;  
            root = root->right;  
            delete del;  
            del = NULL;  
            return true;  
        }  
        else if (root->right == NULL)  
        {  
            del = root;  
            root = root->left;  
            delete del;  
            del = NULL;  
            return true;  
        }  
        else  
        {  
            Node* RightFirst = root->right;  
  
            while (RightFirst->left)  
            {  
                RightFirst = RightFirst->left;  
            }  
  
            swap(root->val, RightFirst->_val);  
  
            Remove(root->right, value);  
            return true;  
        }  
    }  
}