github:代码实现
本文算法均使用python3实现
1. 二叉搜索树定义
二叉搜索树(Binary Search Tree),又名二叉排序树(Binary Sort Tree)。
二叉搜索树是具有有以下性质的二叉树:
(1)若左子树不为空,则左子树上所有节点的值均小于或等于它的根节点的值。
(2)若右子树不为空,则右子树上所有节点的值均大于或等于它的根节点的值。
(3)左、右子树也分别为二叉搜索树。
2. 二叉搜索树的相关操作
2.1 插入操作
从根节点开始,若插入的值比根节点的值小,则将其插入根节点的左子树;若比根节点的值大,则将其插入根节点的右子树。该操作可使用递归进行实现。
程序代码:
def insert(self, root, val):
\'\'\'二叉搜索树插入操作\'\'\'
if root == None:
root = TreeNode(val)
elif val < root.val:
root.left = self.insert(root.left, val)
elif val > root.val:
root.right = self.insert(root.right, val)
return root
2.2 查询操作
从根节点开始查找,待查找的值是否与根节点的值相同,若相同则返回True;否则,判断待寻找的值是否比根节点的值小,若是则进入根节点左子树进行查找,否则进入右子树进行查找。该操作使用递归实现。
程序代码:
def query(self, root, val):
\'\'\'二叉搜索树查询操作\'\'\'
if root == None:
return False
if root.val == val:
return True
elif val < root.val:
return self.query(root.left, val)
elif val > root.val:
return self.query(root.right, val)
2.3 查找二叉搜索树中的最大(小值)
(1)查找最小值:从根节点开始,沿着左子树一直往下,直到找到最后一个左子树节点,按照定义可知,该节点一定是该二叉搜索树中的最小值节点。
程序代码:
def findMin(self, root):
\'\'\'查找二叉搜索树中最小值点\'\'\'
if root.left:
return self.findMin(root.left)
else:
return root
(2)查找最大值:从根节点开始,沿着右子树一直往下,直到找到最后一个右子树节点,按照定义可知,该节点一定是该二叉搜索树中的最大值节点。
程序代码:
def findMax(self, root):
\'\'\'查找二叉搜索树中最大值点\'\'\'
if root.right:
return self.findMax(root.right)
else:
return root
2.4 删除节点操作
对二叉搜索树节点的删除操作分为以下三种情况:
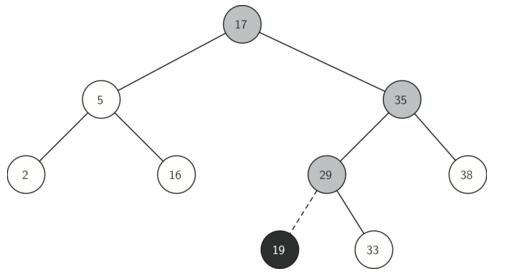
(1)待删除节点既无左子树也无右子树:直接删除该节点即可
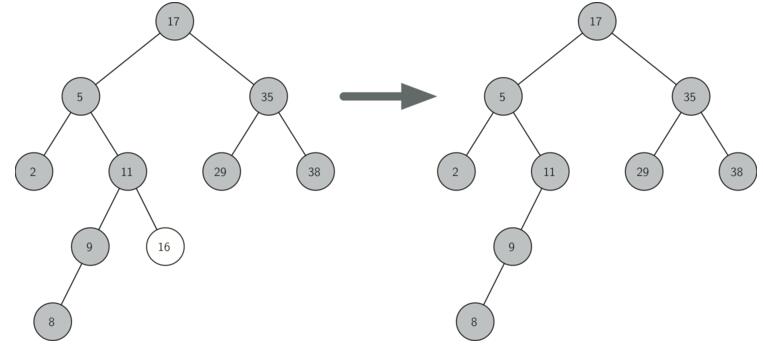
(2)待删除节点只有左子树或者只有右子树:将其左子树或右子树根节点代替待删除节点
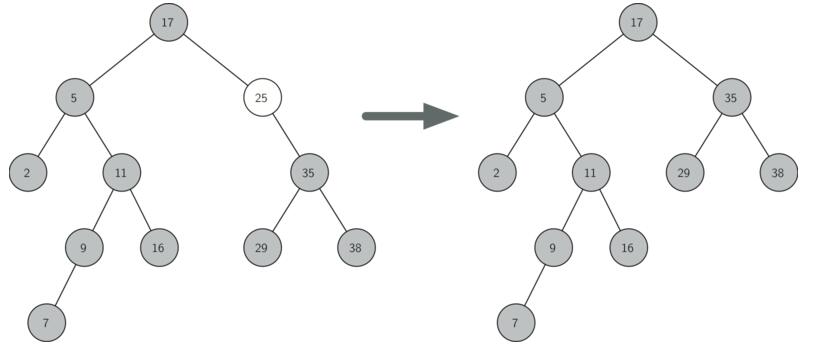
(3)待删除节点既有左子树也有右子树:找到该节点右子树中最小值节点,使用该节点代替待删除节点,然后在右子树中删除最小值节点。
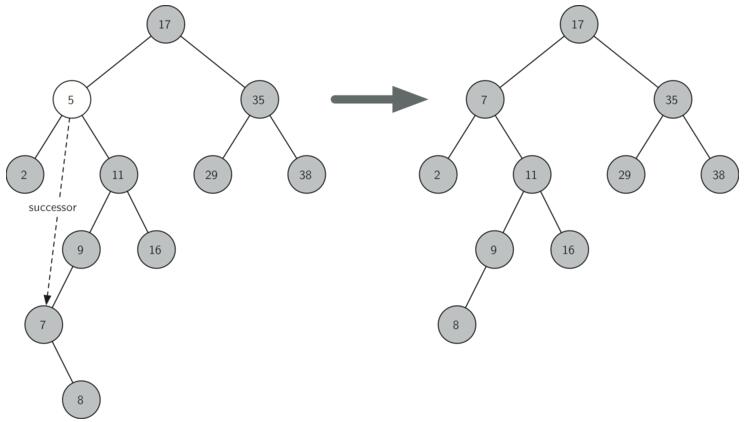
程序代码:
def delNode(self, root, val):
\'\'\'删除二叉搜索树中值为val的点\'\'\'
if root == None:
return
if val < root.val:
root.left = self.delNode(root.left, val)
elif val > root.val:
root.right = self.delNode(root.right, val)
# 当val == root.val时,分为三种情况:只有左子树或者只有右子树、有左右子树、即无左子树又无右子树
else:
if root.left and root.right:
# 既有左子树又有右子树,则需找到右子树中最小值节点
temp = self.findMin(root.right)
root.val = temp.val
# 再把右子树中最小值节点删除
root.right = self.delNode(root.right, temp.val)
elif root.right == None and root.left == None:
# 左右子树都为空
root = None
elif root.right == None:
# 只有左子树
root = root.left
elif root.left == None:
# 只有右子树
root = root.right
return root
2.5 打印操作
实现二叉搜索树的中序遍历,并打印出来。该方法打印出来的数列将是按照递增顺序排列。
程序代码:
def printTree(self, root):
# 打印二叉搜索树(中序打印,有序数列)
if root == None:
return
self.printTree(root.left)
print(root.val, end = \' \')
self.printTree(root.right)
引用及参考:
[1]《数据结构》李春葆著
[2] https://blog.csdn.net/u010089444/article/details/70854510?utm_source=itdadao&utm_medium=referral
写在最后:本文参考以上资料进行整合与总结,属于原创,文章中可能出现理解不当的地方,若有所见解或异议可在下方评论,谢谢!
若需转载请注明:https://www.cnblogs.com/lliuye/p/9118591.html