入门神经网络优化算法：二阶优化算法K-FAC

Posted 2022-11-30 大饼博士X

文章目录

• A block-wise Kronecker-factored Fisher approximation
• Approximating $\tilde{F}$ as block-diagonal
• 参考资料

优化算法系列文章索引：

• 入门神经网络优化算法（一）：Gradient Descent，Momentum，Nesterov accelerated gradient
• 入门神经网络优化算法（二）：Adaptive Optimization Methods：Adagrad，RMSprop，Adam
• 入门神经网络优化算法（三）：待定
• 入门神经网络优化算法（四）：AMSGrad，Radam等一些Adam变种
• 入门神经网络优化算法（五）：二阶优化算法Natural Gradient Descent（Fisher Information）
• 入门神经网络优化算法（六）：二阶优化算法K-FAC
• 入门神经网络优化算法（七）：二阶优化算法Shampoo

上一篇介绍了二阶优化算法Natural Gradient Descent（自然梯度算法），虽然可以避免计算Hessian，但是依然在计算代价上极高，对于大型的神经网络参数规模依然不可能直接计算。本篇继续介绍自然梯度算法后续的一个近似计算方法K-FAC[1]，让自然梯度算法可以（近似）实现。如果还不清楚自然梯度算法，可以回看：入门神经网络优化算法（五）：二阶优化算法Natural Gradient Descent（Fisher Information）

A block-wise Kronecker-factored Fisher approximation

自然梯度的算法关键就是计算Fisher矩阵的逆，$F^{-1}$。首先表示对数似然loss对参数的梯度为（score function）：

vec()表示把一个矩阵向量化，D表示梯度计算。所以可以把Fisher矩阵写成：

$W_i$表示第$i$层的参数矩阵，很容易知道，$D{W}_i=g_i{\bar{a}}_{i-1}^T$，$g_i$表示第$i$层的梯度，${\bar{a}}_{i-1}$表示input。

介绍Kronecker product：

以及一个小性质：$vec(u{v}^T)=v\otimes u$。因此上面的Fisher matrix中的每一个小项可以写成：

这里引入第一次近似：Kronecker product期望近似成期望的Kronecker product。目的是要把$F$每一个小项表示成两个矩阵的Kronecker product。而${\bar{A}}_{ij}$和$G_{ij}$可以用batch的平均来计算。但是这样的近似还是很难算出整个Fisher矩阵。观察Fisher矩阵非对角块，我们可以发现Fisher矩阵建立了各种两两层之间的参数梯度关系。这个和一般的一阶梯度方法就是很大的不同了（类似Hessian矩阵，计算复杂度很大）。

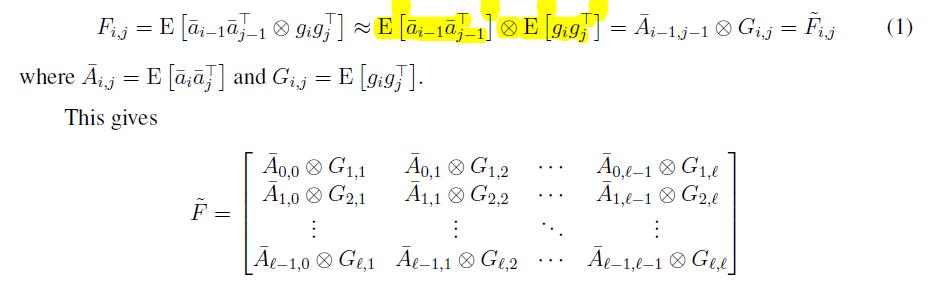
推到这里，还是不能很容易算，接下来引入第二次近似。

Approximating $\tilde{F}$ as block-diagonal

只考虑对角块元素，也就是只在每一个layer内考虑计算FIsher矩阵，这样就变成一个块对角矩阵。我们知道块对角矩阵的逆就很容易求了，只要求每一个块的逆就行了。

Kronecker product还有一个很好用的性质：$(A\otimes B{)}^{-1}=A^{-1}\otimes B^{-1}$，因此我们最后可以得到（近似）Fisher Matrix的逆为：

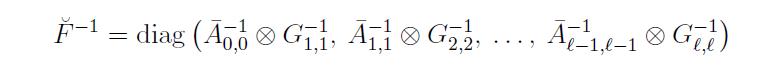
所以，最后我们只要计算${\bar{A}}_{i,j}$和$G_{i,j}$的逆就好了。但是，这样还是要去算Kronecker product，这个感觉还是有点复杂。那么还需要一个很好用的性质：$(A\otimes B)\text{vec}(X)=\text{vec}(BX{A}^T)$

考察任意其中一层$i$，我们实际要算的是$u_i={\tilde{F}}_{ii}^{-1}{g}_{wi}$，我们记$g_{wi}=\text{vec}(V_i)$，$V_i$是梯度矩阵形式，size类比于$W_i$，是i层的outsize*insize。（注意，这里的$g_{wi}$表示$W_i$权重的梯度，前面$g_i$表示的是top-diff）。

我们需要算的最终形式是：$({\bar{A}}_{i-1,i-1}^{-1}\otimes G_{i,i}^{-1})\text{vec}(V_i)=\text{vec}(G_{i,i}^{-1}{V}_i{\bar{A}}_{i-1,i-1}^{-1})$。不考虑等式右边的vec，我们可以得到第$i$层的自然梯度，size类比于$W_i$：

那么自然梯度就可以算了，但是其中有两个比较大的矩阵逆怎么办呢？复杂度也很高啊！这里就没有进一步近似了，参考我的博客：三十分钟理解：矩阵Cholesky分解，及其在求解线性方程组、矩阵逆的应用，用Cholesky分解来求解矩阵逆。所以到这里，我们可以发现，二阶算法即使在一系列近似以后，计算复杂度依然很大，但是K-FAC已经是相对比较容易计算的二阶算法了，有研究工作[2]就利用了K-FAC，并在分布式计算环境下实现算法。只需要35epoch，16K Batchsize下，可以训练ResNet50在ImageNet下达到75%的Top1准确率，效果非常不错。

另外最新的一个工作是[7]，也是用到了K-FAC来训练卷积神经网络。主要参考了[9]中关于preconditioned
gradient计算方案，用特征分解来代替了矩阵求逆。在这里我们再复习一下上面的流程，用[7]中的截图

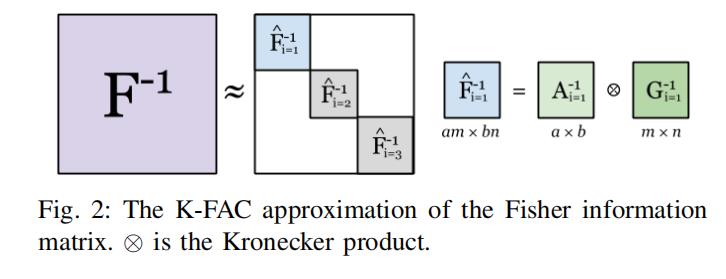
上面公式（13）有一点小问题，应该是$\nabla L_i(w_i^{(k)})$。用特征分解的方法来替换原来对A和G的求逆。

参考资料

[1] Optimizing Neural Networks with Kronecker-factored Approximate Curvature, 2016
[2] 2019 Large-Scale Distributed Second-Order Optimization Using Kronecker-Factored Approximate Curvature for Deep Convolutional Neural Networks
[3] DISTRIBUTED SECOND-ORDER OPTIMIZATION USING KRONECKER-FACTORED APPROXIMATIONS
[4] 2013 Revisiting natural gradient for deep networks
[5] 2014 New insights and perspectives on the natural gradient method
[6] Phd Thesis, James Martens, SECOND-ORDER OPTIMIZATION FOR NEURAL NETWORKS
[7] 2020 Convolutional Neural Network Training with Distributed K-FAC
[8] 2018 an_evaluation_of_fisher_approximations_beyond_kronecker_factorization
[9] 2016 A Kronecker-factored approximate Fisher matrix for convolution layers