神经网络优化算法综述
Posted Young_Gy
tags:
篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了神经网络优化算法综述相关的知识，希望对你有一定的参考价值。
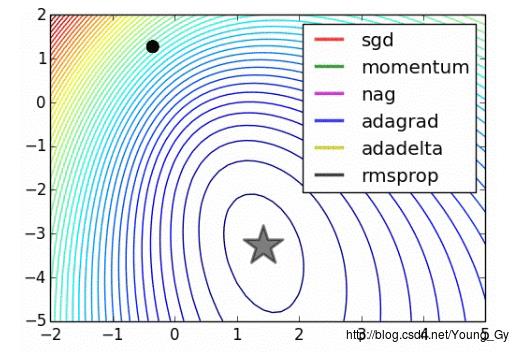
神经网络的训练有不同算法，本文将简要介绍常见的训练算法：adagrad、momentum、nag、rmsprop。同时简要介绍如何进行算法检查。
算法检查
当我们实施了神经网络的梯度算法后，怎么知道我们的算法是否正确。在用于大规模数据之前，需要做两件事：
- gradient check
- sanity check
gradient check
梯度检查，就是检查我们的梯度更新是否正确。具体地，检查分析计算出的梯度与数值梯度是否足够接近。
df(x)dx=f(x+h)−f(x)h(bad, do not use)
df(x)dx=f(x+h)−f(x−h)2h(use instead)
上面显示了两种数值梯度的计算方法，一般采用下面那一种。因为进行泰勒展开后，上面项的误差是 O(h) ，下面项的误差是 O(h2) 。
计算出分析梯度与数值梯度后，需要对两者比较，比较采用相对值如下：
∣f′a−f′n∣max(∣f′a∣,∣f′n∣)
通常来说，1e-4的相对误差对于包含kinks的网络（例如relu）是可以接受的，对大多数网络1e-7的误差是相对较好的。
梯度检查有几点建议：
- 使用双精度
- 观察浮点数的范围，不要太小或者太大，以免超出精度限制
- 注意目标函数中是否存在kinks（relu），如果存在可以减少测试点的数量
- step不是越小越好，过小会遇到数值问题
- 检查的网络状态应该是网络的特征状态，不要在网络初始状态进行检查
- 检查的时候不要让正则项过强，否则会影响盖住data loss
- 关掉dropout等随机机制，对dropout额外进行检测
- 高维数据检测部分维度即可
sanity check
- 随机化数据，看看loss的计算是否符合预期
- 增强正则项，看看loss有没有按照预期增加
- 看看算法是否可以在小的数据集上过拟合
other check
- 更新的大小与原数据大小的比例在1e-3较合适。
# assume parameter vector W and its gradient vector dW
param_scale = np.linalg.norm(W.ravel())
update = -learning_rate*dW # simple SGD update
update_scale = np.linalg.norm(update.ravel())
W += update # the actual update
print update_scale / param_scale # want ~1e-3- 监测每层激活函数以及梯度的分布
- 进行参数可视化
一阶算法
Adagrad
在神经网络的训练中，学习率一般随着迭代次数的增长而下降。通常采用学习率的变化公式为：
ηt=ηt+1‾‾‾‾‾√
可是学习率不仅受时间（迭代次数）的影响，也受当前参数或者说当前参数所在状态的影响。Adagrad便用参数之前导数的rms考虑了参数的状态信息。
令：
gtηtσt=∂C(θt)∂w=ηt+1‾‾‾‾‾√=1t+1∑i=0t(gi)2‾‾‾‾‾‾‾‾‾‾‾‾‾‾⎷
只考虑时间变化的梯度下降与adagrad对比如下：
wt+1wt+1←wt−ηtgt←wt−ηtσtgt
例子如下：
adagrad的解释如下：
群体智能中的联邦学习算法综述---简笔记（除安全类）
MATLAB 求函数极值的内置函数一览表（实则优化算法函数汇总）
MATLAB 求函数极值的内置函数一览表（实则优化算法函数汇总）