最速下降法和牛顿法求解多元非线性函数的最优值

Posted 2022-11-25 墨叔叔

一、问题描述

对于下面的非线性函数使用最速下降法、牛顿法、BFGS法和FR法求解最优值

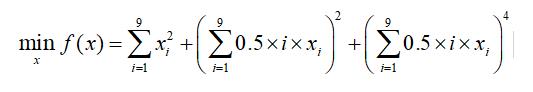
 选择初始点x0=（-5，-4，...，2，3）T，该问题的最优解是X*=0。精度取1e-4，步长取Armijo线搜索。

二、Armijo线搜索

Armijo 准则[1]

将上述判断准则写成代码为：

function new_d=Armijo(x,d,g)
deta = 0.4; % 取值范围为[0,0.5]
beta = 0.2; % 取值范围为[0,1]
m=1;
io = 1; 
G=g';
while io==1
    temp1=f(x+beta^m.*d);
    temp2=f(x)+deta*beta^m*G*d;
    if temp1<=temp2%Armijo准则， f是原目标函数
        io = 0; % 循环break
    else
        m = m+1;
    end
end
new_d=beta^m*d;

[1]张炳杰. 基于广义Armijo线搜索的共轭神经网络算法设计与分析[D].中国石油大学(华东),2019.

三、最速下降法

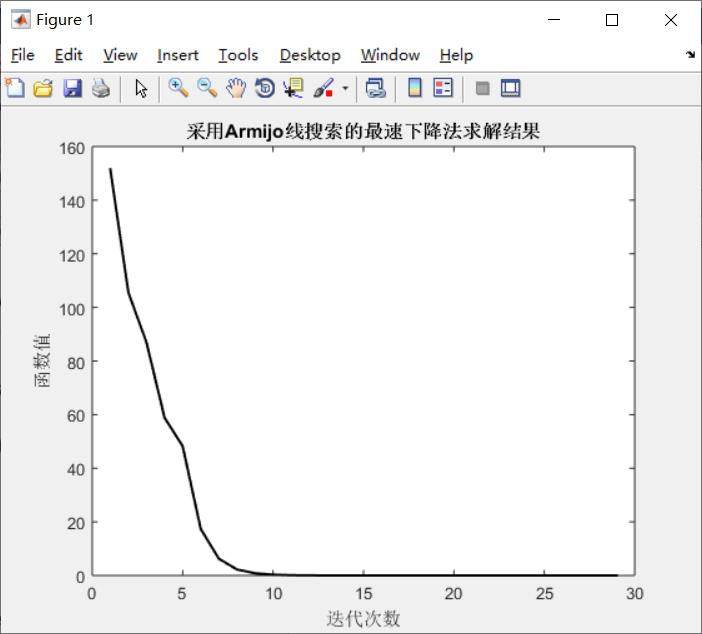
 结果：

 代码：

采用Armijo线搜索的最速下降法求解非线性方程的matlab代码-专业指导文档类资源-CSDN下载

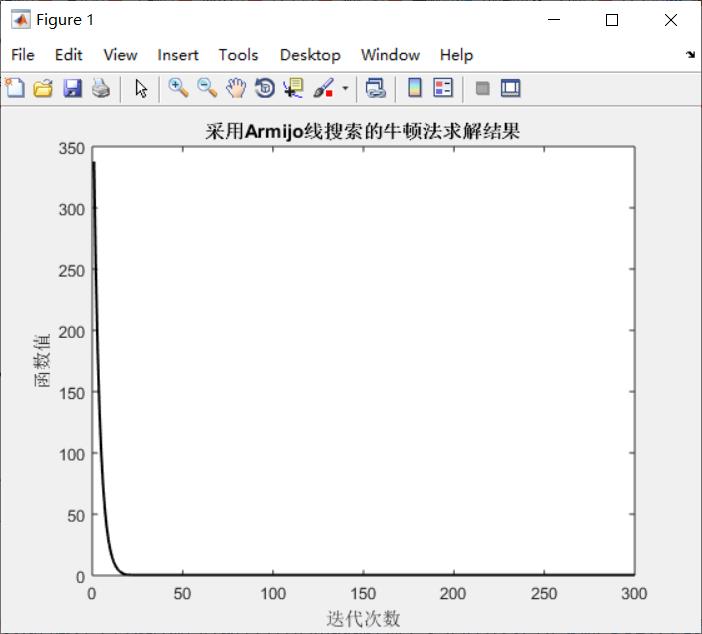
四、牛顿法

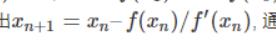
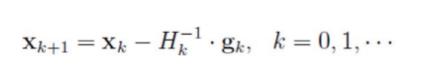
结果：

 代码

 https://download.csdn.net/download/qq_44152192/45709007

五、总结

能够看到最速下降法收敛到相应结果的速度较快，但是牛顿法迭代过程较为平滑，前期收敛快。