基于Armijo搜索步长BFGS法和FR法求解多元非线性函数的最优值

Posted 2022-11-23 墨叔叔

一、问题描述

对于下面的非线性函数使用最速下降法、牛顿法、BFGS法和FR法求解最优值

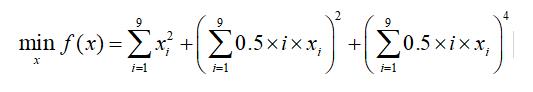
 选择初始点x0=（-5，-4，...，2，3）T，该问题的最优解是X*=0。精度取1e-4，步长取Armijo线搜索。

[1]李菊雯,吴泽忠.基于Armijo搜索步长的BFGS与DFP拟牛顿法的比较研究[J].成都信息工程大学学报,2021,36(05):558-563.

二、BFGS法

 BFGS法求解时第一个近似雅各比矩阵B1可以求解也可以直接使用单位矩阵，因此两个方式都进行尝试得到

B1雅各比矩阵直接求解时：

 B1采用单位矩阵时

 显然第一次求解出雅各比矩阵后的结果较好。

代码

基于Armijo搜索步长BFGS法求解多元非线性函数的最优值-专业指导文档类资源-CSDN下载

三、FR法

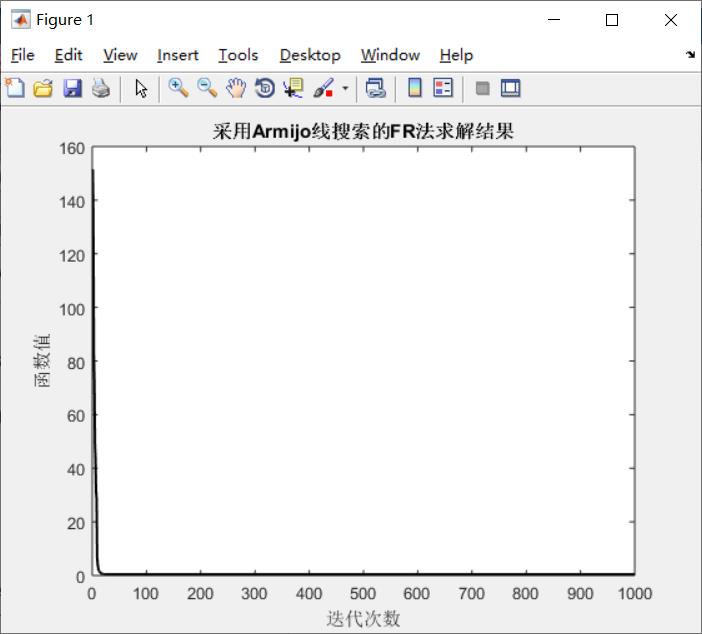
 代码

Armijo线搜索的FR法求解非线性函数结果-专业指导文档类资源-CSDN下载