概率图模型

Posted 2022-08-18 Debroon

概率图模型

• 前置知识
• • 概率论基础
  • 图论基础
• 表示方式
• • 贝叶斯网络
  • • 联合概率为什么可以表示为局部条件概率表的乘积？
  • 马尔可夫随机场
  • 因子图
• 推理方法
• • 推理问题分类 & 变量消元法
  • 团树传播算法
  • 信念传播算法
  • 二值图切法
  • 基于图切法的近似推理
  • 信念传播算法的能量最小解释
• 俩类学习
• • 结构学习
  • 参数学习
• 应用
• • 条件随机场在自然语言处理中的应用
  • 概率图模型在医学图像中的应用
  • 概率图模型在计算机视觉中的应用

 

---

前置知识

概率图模型是概率论和图论结合的产物，用图的节点表示变量（状态），图的边表示局部变量（状态）间的概率依赖关系。

假设每个状态的转移概率只取决于相邻的状态，将现实问题抽象为概率模型，使得归结为计算概率模型里面某些变量的概率分布。

 

---

概率论基础

• 记录在《论概率：从局部随机性到整体确定性》

概率图模型常用的三个概念：联合概率分布、边缘分布、最大后验概率状态。

联合概率分布、边缘分布，如下图：

联合概率分布是二维随机变量组成 (X,Y)，整个红色区域就是联合概率分布，如当 $X=x_1、Y=y_1$ 时，联合概率是 $\frac{4}{32}$。

求联合分布概率：

• 写出 X 的所有可能情况
• 写出 Y 的所有可能情况
• 列出表

 

边缘分布是只看当前变量的分布情况，比如变量为 $y_1$，边缘分布就是把第一行的概率全部相加（$\frac{4}{32}+\frac{2}{32}+\frac{1}{32}+\frac{1}{32}=\frac{8}{32}$），如果变量是 $x_1$，就是把第一列的概率相加。

求边缘分布概率：

• 公式为：$P(y_1)=P(y_1,x_1)+P(y_1,x_2)+P(y_1,x_3)+P(y_1,x_4)$

 

最大后验概率状态，如下图：

图上的曲线是联合概率分布的取值，我们找联合分布中的最大值。

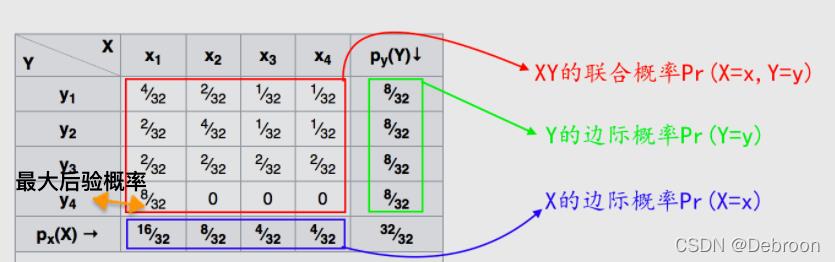
当 $X=x_1、Y=y_4$，$P_{max}(X,Y)=\frac{8}{32}$。
 

---

图论基础

• 可参考图论专栏。

无向图是没有方向的，顶点之间只要有边，就可以相互走通，如左图可以 A->D，也可以 D->A。

有向图存在方向，比如右图可以 D->A，但 A 不能到 D。
 

---

表示方式

概率图模型的表示主要是：贝叶斯网络、马尔可夫随机场、因子图。

• 贝叶斯网络：联合概率分布表示为，每个节点的条件概率的联乘积
• 马尔科夫随机场：联合概率分布表示为，节点的势函数和边的势函数的联乘积
• 因子图：联合概率分布表示为，因子的联乘积

这些模型刻画了随机变量的依赖关系，反映了问题的概率结构，为推理算法提供了数据结构。

概率图模型主要研究问题是：

• 为什么联合概率分布可以表示为局部势函数的联乘积？（条件独立性）
• 如何在图模型建模中引入先验知识？

 

---

贝叶斯网络

贝叶斯网络的建模，采用的是一种因果图的模型。

• 一个简单的因果模型，就能胜过无数经验。

假设咱们要研究一个死刑。总共有五个变量 ——

1.法庭 CO 是否判决死刑

2.队长 C 是否下令开枪

3.士兵 A 是否开枪

4.士兵 B 是否开枪

5.犯人 D 是否死亡

这五个变量的值都是1或者是0，1表示肯定，0表示否定。

如果法庭判决了，但是队长不下令，犯人会不会死？这种事情从来没发生过，机器学习、大数据在这里用不上。但是如果你承认这里面有因果关系，咱们就可以画一张因果关系图 ——

图中每个箭头代表一个因果关系，从缘故指向结果。

现在犯人已经死了。犯人家属找到士兵 A，说你当初要是不开枪，他就不会死！士兵 A 不需要考察什么大数据，他马上就可以拿出这张因果关系图，说你看，命令已经下达了，就算我不开枪，士兵 B 也会开枪，犯人还是会死啊。

你要想让犯人不死，你得说服法庭不判决，或者说服队长不下令，或者同事说服 A 和 B 两人都不开枪才行啊！

你看这是多么清楚的分析。机器学习、大数据不能告诉你这些，但是因果关系可以告诉你。

 
第一个使用因果模型图搞研究的，是美国统计学家休厄尔·赖特（Sewall Wright）。

1920年，赖特发表了一篇有关天竺鼠的毛色遗传的论文。他假设有三种因素可能影响毛色，分别是发展（d）、遗传（h）和环境（e），他把这三种因素画成了因果关系图 ——

然后赖特根据自己的实验结果，用解方程的方法算出了三种因素的相对大小 — 他把天竺鼠的毛色问题给解决了。

使用因果模型，解决问题的步骤就是下面这样的：

• 第一步，根据你自己的见识（专家经验），画一张主观的因果模型图。模型里有些因果关系是概率性的，A 发生并不一定会让 B 发生，只要 A 对 B 有影响就行。

• 第二步，使用实验和数据分析，确定图中每个因果关系的强弱大小。这样你就有了一个完整的因果模型。

• 第三步，使用因果模型，让机器拥有人的智能（因果思维、分析、假设、推理、演绎、归纳等）。

虽然因果模型很强大，但是因果模型有一个大问题，在哲学、数学等科学领域，你的科学方法得客观，每个人都经验不一样，那肯定不能被认可。

传统的科学方法，是

1.提出一个理论假设；

2.做实验验证；

3.如果实验结果符合理论，这个理论就暂时站得住脚，如果不符合，理论就被证伪了。

这是非黑即白的剧情，理论要么就继续保留，要么就彻底抛弃。

不过，我们发现数学上的贝叶斯方法则不同，是先给理论假设设定一个可信度。新证据并不直接证实或者证伪理论，只是调整可信度的大小，做一个动态的判断。

贝叶斯方法视角的科学方法：

1.先评估一下自己的信念，设定 P(信念)；

2.等待新证据；

3.证据出来以后，用贝叶斯公式更新自己的信念，计算 P(信念|证据)；

4.继续等待新证据……

保持开放心态，让你的观点随事实发生改变，用一个量化的数值决定你的判断。虽然永远都摆脱不了主观的成分，但是你会做出更科学的决策。

1982年，机器学习开山鼻祖·珀尔把贝叶斯方法和因果模型的组合引入了人工智能领域，发明了“贝叶斯网络”。

贝叶斯网络的表现形式，因为采用了图的结构（有向无环图），用节点边的相互关系（有向边的父节点指向孩子节点）。

这样的好处是，构建这个网络的参数很少，计算量也小。

概率问题、图论建模，归根结底我们想要解决复杂的概率问题。

这个概率问题一定是多变量（因素，要素）相互影响的问题。

那么这个复杂的问题怎么才能理清各个变量间的概率影响关系呢

• 1.使用贝叶斯网络建模，建模每个事件/变量（因素）为一个节点，节点间互相影响用箭头表明
• 2.可以将整个问题的联合概率分布写成每个节点于其父节点条件概率分布连乘积的形式（为什么可以这样写？ 因为条件独立性）

举个例子。

对一个学生能否拿到老师的推荐信这一问题进行建模研究。

假设与该问题相关的变量有以下五个：

• 试题难度 Difficulty
• 学生智力 Intelligence
• 考试成绩 Grade
• 高考成绩 SAT
• 是否得到老师推荐信 Letter

如何用贝叶斯网络对该问题进行建模表示

• 如何定义节点?
• 如何定义节点之间的概率依赖关系?
• 如何表示联合概率分布?

那如何定义节点?
比如试题难度 Difficulty 有俩种情况：低难度 $d^0$、高难度 $d^1$。

 
那如何定义节点之间的概率依赖关系? 这需要我们按照自己的经验，画出因果模型：

这个模型怎么看呢？

• 如考试成绩 Grade 受俩个要素影响：试题难度 Difficulty、学生智力 Intelligence
• 试题难度 Difficulty 分为俩种情况，低难度的概率为 0.6，高难度的概率为 0.9

 
那如何表示联合概率分布? 按照图的指向，写成数学形式：

有了这个数学形式后，我们即可计算出这五个变量取某个值的时候，分析这种情况的可能性有多大。

比如，试题难度高、学生智力低、考试成绩高、高考成绩高、拿到老师推荐信这种情况。

和我们的常识一样，这种情况的可能性很低。

 

联合概率为什么可以表示为局部条件概率表的乘积？

这是一个贝叶斯网络。

熬夜会增加赖床概率，赖床会增加迟到概率。

已知发生赖床，问这个人熬夜，是否会影响到迟到？

补充概率知识：

• 变量独立性
  

• 条件独立性
  

核心问题，为什么可以将整个问题的联合概率分布写成每个节点于其父节点条件概率分布连乘积的形式。

为什么可以这样写？ 因为条件独立性。

关于三个变量的联合概率分布，有一个链式法则：

再把 $P(B|A,C)=P(B|C)$ 代入：

这就是贝叶斯网络定义的式子（因子分解形式）。

 

---

马尔可夫随机场

 

---

因子图

 

---

推理方法

概率推理相当于模型求解，概率推理的方法分为三类。

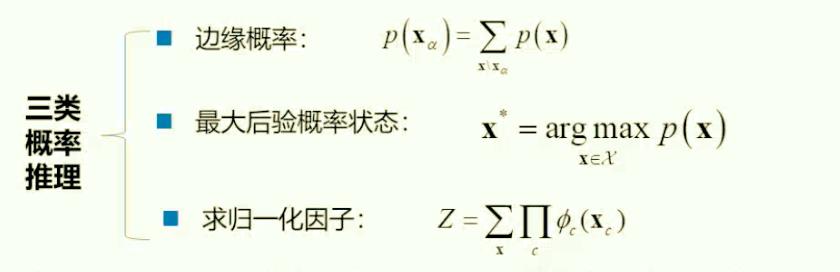
推理方法分为：精确推理、近似推理。
 

---

推理问题分类 & 变量消元法

 

---

团树传播算法

 

---

信念传播算法

 

---

二值图切法

 

---

基于图切法的近似推理

 

---

信念传播算法的能量最小解释

 

---

俩类学习

有一些情况下概率图模型需要进行学习 — 对于复杂、缺失专家经验的概率模型，如果有一定数量的观测数据，通常希望能够从观测数据中获得模型的参数甚至结构。

• 参数学习是通过图模型的结构（节点和边），学习模型的参数。

• 结构学习是从数据中推断变量之间的依赖关系（学习结构，有哪些节点和边）。

 

---

结构学习

 

---

参数学习

 

---

应用

概率图模型在图像分割时的应用，如一张牛吃草的图片，我们通过颜色是来进行分割，牛的颜色、草的颜色是不同的。

相邻像素点的像素值具有连续性（相似性），赋予概率意义，就可以进行概率推理，推理的结果就是图像分割的结果。

 

---

条件随机场在自然语言处理中的应用

 

---

概率图模型在医学图像中的应用

 

---

概率图模型在计算机视觉中的应用