使用神经网络实现对天气的预测

Posted 2022-08-05 Alan and fish

1.神经网络原理简单理解

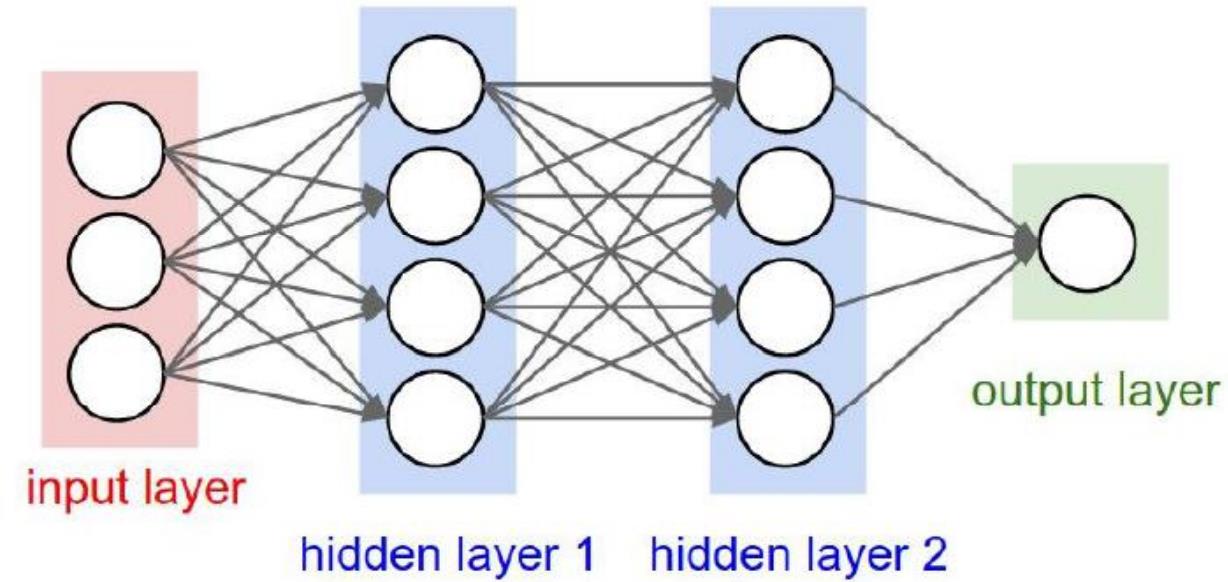
如图所示这个神经网络分为:

• 输入层
  其中的输入层的每一个节点代表的是一个对象的其中的一个特征，这个些特征可以用一个矩阵x表示，因为这是我们人类看的懂的东西，所以要转换成计算机看的懂的东西。
  使用函数进行计算，w是权重，b是偏置。

y=w₁x+b₁

我们通过不断的训练这个函数，通过反向传播进行梯度下降的到最好的w和b能够拟合这些数据。
其中输如层有3个节点是一个1x3的矩阵，对应的隐藏是一个1x4的矩阵，则要乘以w₁是一个3x4的矩阵，b是一个1x4的矩阵。
其中神经网络还需要一个激活函数，常用的有的sigmoid，relu，tanh，因为神经网络对应的是一个线性化的函数，我们有的时候要解决非线性化的问题，所以引入激活函数，解决线性模型不能解决的问题。

• 隐藏层

• 输出层

总而言之，神经网络就是找到最合适的w和b使得其函数图形能够包含我们需要的样本点。如图所示，我们的神经网络的图形就是绿色的，正好包含了所有的正例，等我下次预测的时候，也就是把特征丢进去，他就会输入一个在绿色图像的点。

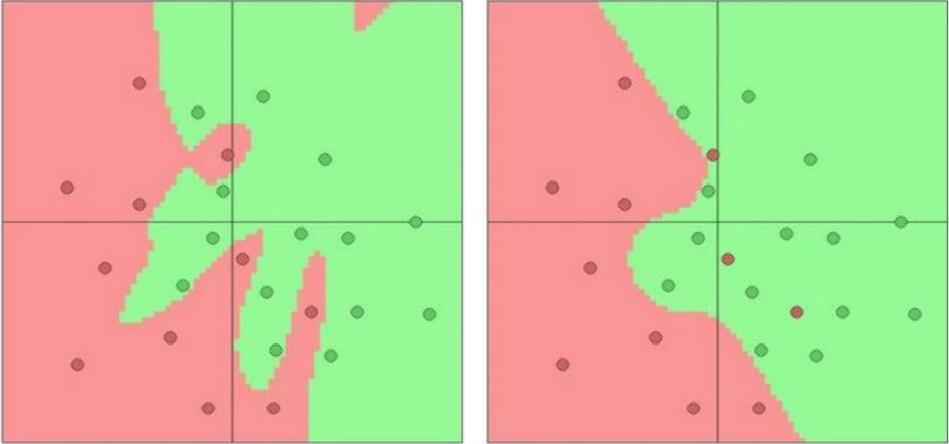
这块有点讲解的不是很清楚，大家可以参考一下其他网上的帖子。

2.使用神经网络预测天气案例

为了更好的学习神经网络，我学习了一个例子。
这个例子的数据集是348天的天气情况，根据这些天气情况的特征进行预测。
数据集：

链接：https://pan.baidu.com/s/1NORkTP-OFOfsbRVvyt29sw
提取码：kibn

• 加载数据

import numpy as np
import pandas as pd
import datetime
import matplotlib.pyplot as plt
from sklearn import preprocessing

# 加载数据
def data_load(filepath):
    '''数据表中
    year,moth,day,week分别表示的具体的时间
    temp_2：前天的最高温度值
    temp_1：昨天的最高温度值
    average：在历史中，每年这一天的平均最高温度值
    actual：这就是我们的标签值了，当天的真实最高温度
    friend：这一列可能是凑热闹的，你的朋友猜测的可能值，咱们不管它就好了'''
    features=pd.read_csv(filepath)
    # 打印数据格式
    print(features.head())
    print(features.shape) # 一共有348条数据
    return features

得到的数据是当前天气,前天,昨天的天气,数据如下

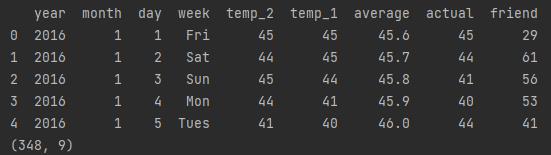
• 展示数据
  为了让大家更好的了解数据的情况,做了一个可视化展示现在所有的数据

def showpicture(features):
    # 处理时间数据
    years = features['year']
    months = features['month']
    days = features['day']

    # 转换成datetime格式
    dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in
             zip(years, months, days)]
    # 将string格式的按照要求转换成时间格式
    dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]
    # print(dates[:5])
    # 独热编码
    # 因为我们的数据中的星期是字符串格式,所以将星期做一个独热编码就会转换成对应的数据
    features = pd.get_dummies(features)
    # print(features.head(5))

    # 将数据画成图片
    # 指定默认风格
    plt.style.use('fivethirtyeight')

    # 设置布局
    fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize=(10, 10))
    fig.autofmt_xdate(rotation=45)  # 表示对图中的x轴进行45度的翻转

    # 标签值(实际值)
    ax1.plot(dates, features['actual'])
    ax1.set_xlabel('day');
    ax1.set_ylabel('Temperature');
    ax1.set_title('Max Temp')

    # 昨天
    ax2.plot(dates, features['temp_1'])
    ax2.set_xlabel('day');
    ax2.set_ylabel('Temperature');
    ax2.set_title('Previous Max Temp')

    # 前天
    ax3.plot(dates, features['temp_2'])
    ax3.set_xlabel('day');
    ax3.set_ylabel('Temperature');
    ax3.set_title('Two Days Prior Max Temp')

    # 我的朋友
    ax4.plot(dates, features['friend'])
    ax4.set_xlabel('day');
    ax4.set_ylabel('Temperature');
    ax4.set_title('Friend Estimate')
    plt.show()

如图所示,对应的是当前最高气温、昨天最高气温、前天最高气温，其中的朋友预测的天气可以忽略不看。

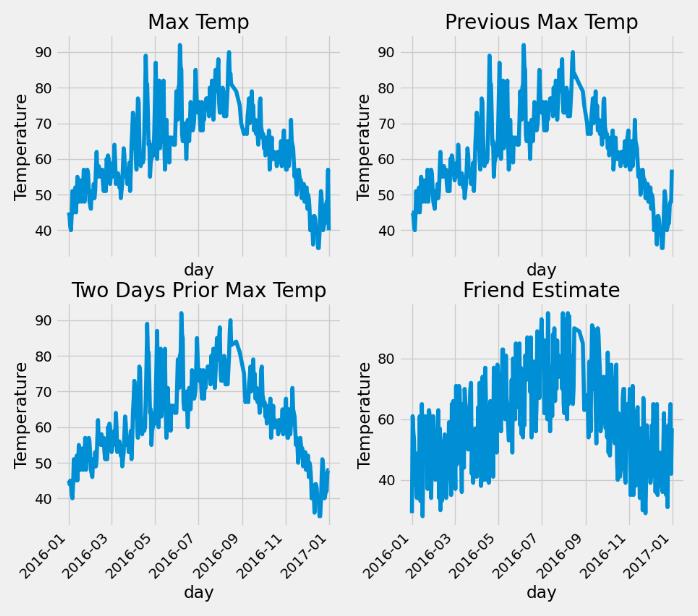
• 处理数据

# 处理数据
def data_handle(features):
    # 独热编码
    # 因为我们的数据中的星期是字符串格式,所以将星期做一个独热编码就会转换成对应的数据
    features = pd.get_dummies(features)

    # 标签
    # 在我们的数据中,除开actual是一个我们实际值y,其他的值都是x
    # 所以当读把他抽取出来
    labels=np.array(features['actual'])
    # print(labels)

    # 在特征中去掉标签
    features=features.drop('actual',axis=1)

    # 名单单独保存一下,以备后患
    features_list=list(features.columns)
    print(features_list)

    # 将数据转换成合适的格式
    features=np.array(features)
    # print(features)
    # print(features.shape)

    # 因为我们的原始数据中的month和day都比较小,所以我可以对features做一个标准化,这样到时候训练收敛会更快一些
    input_features=preprocessing.StandardScaler().fit_transform(features)

    return input_features,labels

• 训练模型预测天气
  这里是初学神经网络，所以就把训练集当作测试集，然后通过图像展示，更加直观的看到预测的数据的拟合程度。

import torch
from data_load.preprocessdata import data_load,data_handle,showpicture
from model.modeling import Neural
import torch.nn as nn
import numpy as np
import datetime
import pandas as pd
import matplotlib.pyplot as plt

if __name__=='__main__':
    # 加载数据
    features=data_load('./data/temps.csv')
    # 将数据生成统计图
    # showpicture(features)
    # 将真实值和预测数据分离开
    input_features,labels=data_handle(features）
    # 使用torch.nn构建神经网络
    x = torch.tensor(input_features, dtype=float)
    y = torch.tensor(labels, dtype=float)
    # 设置参数
    input_size=input_features.shape[1] # (348,14),原始数据是一个348行14列的矩阵
    hidden_size=128
    output_size=1
    batch_size=16 # 分批次训练,每次使用16个数据
    my_nn=nn.Sequential(
        nn.Linear(input_size,hidden_size), # 输入层有14个节点,隐藏层有128个节点
        nn.Sigmoid(),# 激活函数使用的是sigmoid函数
        nn.Linear(hidden_size,output_size), # 输出层
    )
    # 定义损失函数,使用的是均方损失函数
    cost=nn.MSELoss(reduction='mean')
    # 构造一个优化器,可以减少输入数据的噪音,使得数据更加便于训练
    optimizer=torch.optim.Adam(my_nn.parameters(),lr=0.001)

    # 训练网路
    losses=[]
    for i in range(1000):
        batch_loss=[]
        # 使用MINI-Batch方法来进行训练
        for start in range(0,len(input_features),batch_size):
            end=start+batch_size if start+batch_size<len(input_features) else len(input_features)
            xx=torch.tensor(input_features[start:end],dtype=torch.float,requires_grad=True)
            yy=torch.tensor(labels[start:end],dtype=torch.float,requires_grad=True)
            ## 训练
            prediction=my_nn(xx)
            loss=cost(prediction,yy)
            optimizer.zero_grad()
            loss.backward(retain_graph=True)
            optimizer.step()
            batch_loss.append(loss.data.numpy())

        # 每100次打印一次损失
        if i%100==0:
            losses.append(np.mean(batch_loss))
            print(i,np.mean(batch_loss))

    # 测试训练结果,原本是要使用测试集的,为了快速实验,我们实验的就是测试集的数据
    x=torch.tensor(input_features,dtype=torch.float)
    predict=my_nn(x).data.numpy() # 需要将tensor数据转换成numpy格式的数据,因为在plt中只支持numpy格式的数据

    # 将预测的数据和实际数据可视化
    # 格式转换
    # 转换成datetime格式
    # 处理时间数据
    years = features['year']
    months = features['month']
    days = features['day']
    dates = [str(int(year)) + '-' + str(int(month)) + '-' + str(int(day)) for year, month, day in
             zip(years, months, days)]
    # 将string格式的按照要求转换成时间格式
    dates = [datetime.datetime.strptime(date, '%Y-%m-%d') for date in dates]

    # 创建一个表格来存储日期和其对应的标签
    true_date=pd.DataFrame(data='date':dates,'actual':labels)

    # 同理创建一个表来存储预测的值
    prediction_data = pd.DataFrame(data='date': dates, 'prediction': predict.reshape(-1))

    # 创建图像
    # 真实值
    plt.plot(true_date['date'],true_date['actual'],'b-',label='actual')

    # 预测值
    plt.plot(prediction_data['date'],prediction_data['prediction'],'ro',label='prediction')
    plt.legend()

    # 图名
    plt.xlabel('Date');
    plt.ylabel('Maximum Temperature(F)');
    plt.title('Actual and predicted Values');
    plt.show()

每100次显示一次的loss：

100 37.94807
200 35.65217
300 35.278557
400 35.112137
500 34.977985
600 34.857384
700 34.736656
800 34.610817
900 34.47966

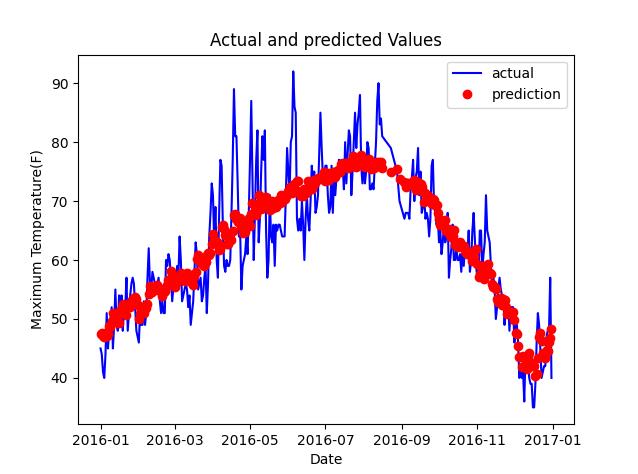
使用matplotlib.pyplot可视化我们预测的天气与真实天气的拟合情况：

3.总结

通过这个小实验,让我简单的理解了神经网络就是一个一个数学函数,训练这个模型就是找到最合适的参数,能够使这些函数完美的包含我们的样本点,下次预测的时候,就将特征输入进去,就能够通过函数计算出哪个y,就是我们预测值.