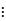运用自回归滑动平均模型灰色预测模型BP神经网络三种模型分别预测全球平均气温，并进行预测精度对比（附代码数据）

Posted 带我去滑雪

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了运用自回归滑动平均模型灰色预测模型BP神经网络三种模型分别预测全球平均气温，并进行预测精度对比（附代码数据）相关的知识，希望对你有一定的参考价值。

        大家好，我是带我去滑雪，每天教你一个小技巧！全球变暖是近十年来，人们关注度最高的话题。2022年夏天，蔓延全球40℃以上的极端天气不断刷新人们对于高温的认知，人们再也不会像从前那样认为全球变暖离我们遥不可及。在此背景下，基于1880年-2022年全球平均气温时间序列数据，分别构建出ARIMA(3,1,2)自回归模型、灰色预测模型、BP神经网络三种模型，并分别对2050、2100年全球平均温度进行了预测，并将三种预测模型的预测效果进行了对比，文中所用数据和代码均可在文末获取。

目录

 1   模型介绍

1.1  自回归滑动平均模型

 1.2  灰色预测模型

1.3 BP神经网络模型

 2  结果分析

2.1  数据可视化

 2.2  自回归移动平均模型及预测

2.2.1 全球平均温度变化趋势分析

2.2.2  一阶差分

 2.2.3  判断ARIMA自相关模型参数

 2.2.4  利用ARIMA自相关模型进行预测

 2.3  GM(1,1)模型预测

2.3.1 GM(1,1)模型建立与检验

2.3.2 GM(1,1)模型预测结果分析

 2.4 BP神经网络模型预测

2.4.1 BP神经网络训练

 3 三种模型预测比较

 1   模型介绍

1.1  自回归滑动平均模型

        差分运算可以提取确定性的信息，一些非平稳序列差分后会显示出平稳序列的性质，此时这个序列也被称为差分平稳序列，可用ARIMA模型进行拟合。具有如下结构的模型被称为求和自回归移动平均模型，简记为ARIIMA（p,d,q）模型：

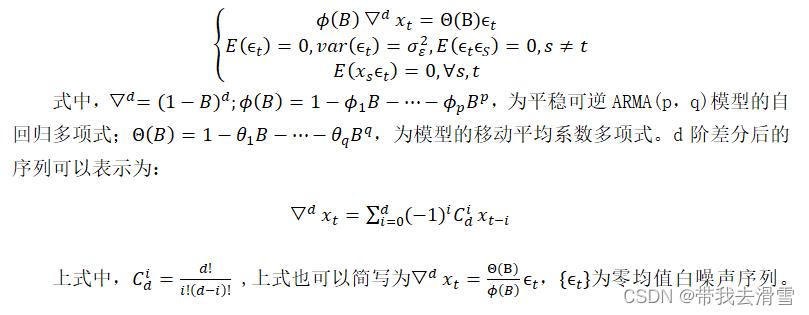
 1.2  灰色预测模型

       灰色预测模型（GM）的主要特点是模型使用的不是原始数据序列，而是生产的数据序列。其核心体系是灰色模型，即对原始数据作累加生成得到近似的规律，建立有规律的生成数列的回归方程，并应用该方程对研究对象动态发展趋势进行预测。再进行建模型。本文选取灰色预测模型中的GM(1,1)，GM(1,1)灰色预测模型以时间序列数据为基础，它表示模型是一阶微分方程，并且只含有一个变量。

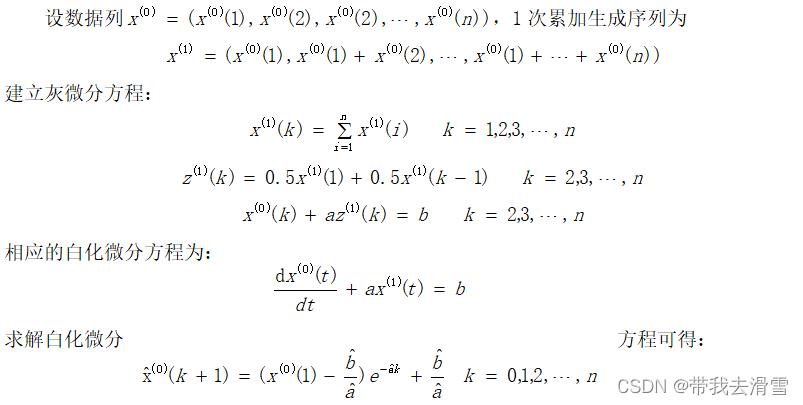
     通过GM(1,1)模型就可指定时区内的预测值，根据实际问题需要，给出相应的预测。

1.3 BP神经网络模型

       BP神经网络是一种多层前馈神经网络，该网络的主要特点是信号向前传递，误差反向传播。在向前传递中输入信号从输入层经隐含层逐层处理，直至输出层，每一层的神经元状态只影响下一层的神经元状态。如果输出层得不到期望输出，则再反向传播，根据预测误差调整网络权重和阈值，从而使BP神经网络预测输出不断逼近期望输出。BP神经网络的拓扑结构如图1所示。

 2  结果分析

2.1  数据可视化

       利用1880-2022年全球平均气温数据，通过R画出了全球平均气温逐年数据序列图和近十年全球平均气温变化图，分别如图2、图3所示。

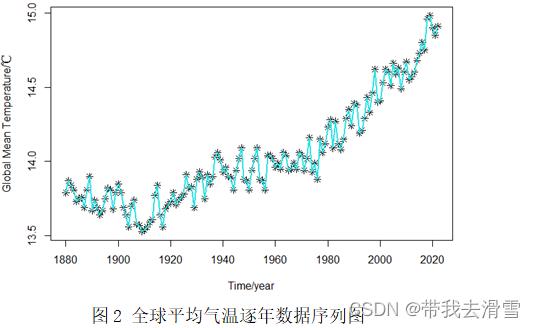
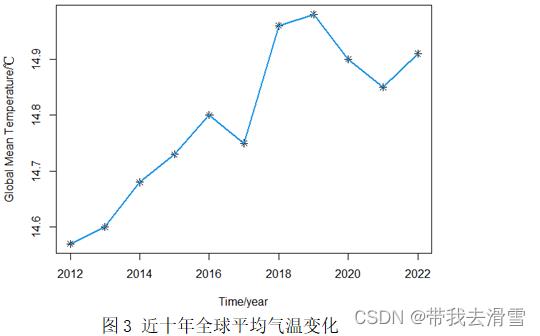
        通过图2和3可以看出，全球平均气温从总体上呈现递增趋势，特别是1960年到2022年，其增长幅度与1960年以前相比更大。2022年3月的全球平均气温达到14.91℃，结合最近十年的全球平均气温变化，我们可以得出2022年3月全球气温的升高导致了比以往10年期间观察到的全球平均气温具有更大的增长。

 2.2  自回归移动平均模型及预测

2.2.1 全球平均温度变化趋势分析

      通过图2可以看出，该时间序列数据具有递增趋势，表现为不平稳。

2.2.2  一阶差分

     将全球平均气温数据进行一阶差分，差分后的序列趋于平稳，其结果见图4所示。

 2.2.3  判断ARIMA自相关模型参数

       一阶差分后序列的自相关系数与偏自相关系数见图5，结合图像特征，尝试用ARIMA(0,1,1)、ARIMA(2,1,1)、ARIMA(3,1,2)模型进行拟合。通过AIC准则和BIC准则对三个模型进行评估，最终选取ARIMA(3,1,2)模型进行预测。

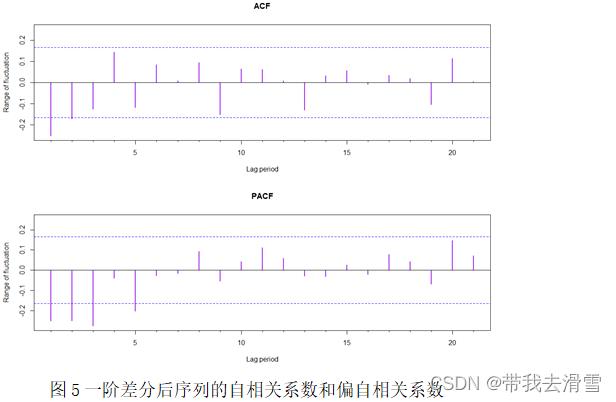
 2.2.4  利用ARIMA自相关模型进行预测

       利用ARIMA(3,1,2)模型预测分别预测2050年、2100年的全球平均温度分别为15.12℃、15.51℃，达不到20℃。各自的预测图像见图6、图7。

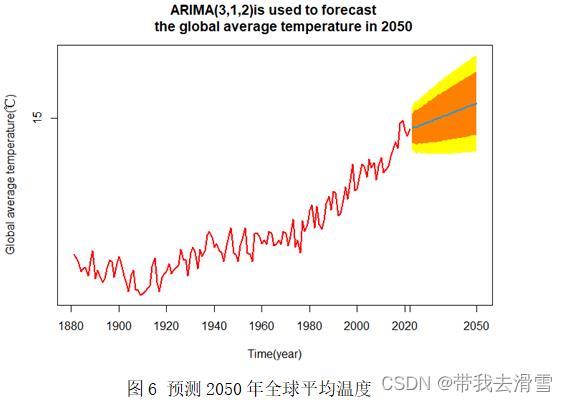
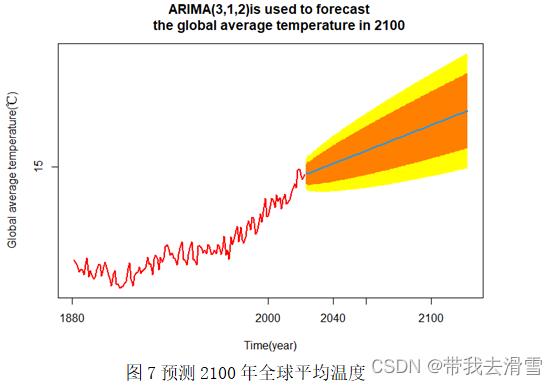
 数据可视化代码

setwd("D:/Desktop")

#1880开始

data<-read.csv("shuju.csv",header=TRUE,sep=',',fileEncoding='utf-8')

wendu<-ts(data$Average,start = 1880,frequency = 1)

plot(wendu,type="p",pch=8,xlim=c(1880,2022),xlab ="Time/year", ylab ="Global Mean Temperature/℃")

lines(wendu,col=5,lwd=2)

#2012开始

data<-read.csv("12.csv",header=TRUE,sep=',',fileEncoding='utf-8')

wendu<-ts(data$Average,start = 2012,frequency = 1)

plot(wendu,type="p",pch=8,xlim = c(2012,2022),xlab ="Time/year", ylab ="Global Mean Temperature/℃")

lines(wendu,col=4,lwd=2)

ARIMA时间序列模型代码

install.packages("fUnitRoots")

install.packages("tseries")

install.packages("forecast")

library(forecast)

library(tseries)

library(fUnitRoots)

mydata=read.csv("C:/Users/hasee/Desktop/data.txt")

sjxlmydata=ts(mydata,start=1881,end = 2022,frequency = 1)

sjxlmydata

plot.ts(sjxlmydata,xlab = "Time(year)",col="blue",ylab = "Global average temperature(℃)",

        main="Global annual mean temperature time series")

length(sjxlmydata)

unitrootTest(sjxlmydata)

dsjxlmydata=diff(sjxlmydata)

dsjxlmydata

plot.ts(dsjxlmydata,xlab = "Time(year)",col="blue",ylab = "The global average temperature after one difference(℃)",

        at=c(1880,1900,1920,1940,1960,1980,2000,2020,2022),main="Differential time series of global annual mean temperature")

axis(side = 2,at=c(-0.2,-0.1,0,0.1,0.2))

Acf(dsjxlmydata,col="purple",lwd=2,,xlab = "Lag period",ylab = "Range of fluctuation",main="ACF")

Pacf(dsjxlmydata,,col="purple",lwd=2,,xlab = "Lag period",ylab = "Range of fluctuation",main="PACF")

unitrootTest(dsjxlmydata)

library(forecast)

fit=auto.arima(sjxlmydata)

fit

qqnorm(fit$residuals)

qqline(fit$residuals)

forecast(fit,28)

plot(forecast(fit,28),col="red",at=c(1880,1900,1920,1940,1960,1980,2000,2020,2022,2050),lwd=2,xlab = "Time(year)",

     main="ARIMA(3,1,2)is used to forecast

     the global average temperature in 2050",ylab = "Global average temperature(℃)",shadecols="oldstyle",axis=(40))

axis(side = 2,at=c(0,5,10,15,20))

plot(forecast(fit,100),col="red",at=c(1880,920,960,2000,2040,2060,2100),lwd=2,xlab = "Time(year)",

     ,main="ARIMA(3,1,2)is used to forecast

     the global average temperature in 2100",ylab = "Global average temperature(℃)",shadecols="oldstyle",axis=(40))

axis(side = 2,at=c(0,5,10,15,20))

plot(forecast(fit,652),col="red",at=c(1880,1980,2080,2200,2300,2400,2500,2600,2674),lwd=2,xlab = "Time(year)",

     main="

Arima (3,1,2) model is used to predict when the

     global average temperature will reach 20 °C",ylab = "Global average temperature(℃)",shadecols="oldstyle",axis=(40))

axis(side = 2,at=c(0,3,6,9,12,15,18,20))

abline(v=2672,h=20,lty=2,col="purple")

library(forecast)

library(tseries)

library(fUnitRoots)

mydata=read.csv("C:/Users/hasee/Desktop/data1.txt")

sjxlmydata=ts(mydata,start=2023,end=2267,frequency = 1)

sjxlmydata

plot.ts(sjxlmydata,xlab="Time(year)",col="blue",ylab="Global average temperature(℃)",lwd=2,at=c(2023,2050,2100,2150,2200,2268),main="BP neural network predictive value")

axis(side=2,at=c(0,3,6,9,12,15,18,20))

abline(v=2268,h=20,lty=2,col="purple")

 2.3  GM(1,1)模型预测

2.3.1 GM(1,1)模型建立与检验

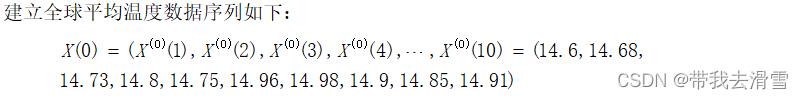
        利用Python进行编程，实现GM(1,1)模型，模型的各种检验指标的计算结果见表1。经过验证，该模型的精度较高，可以进行预测。

表1 GM(1,1)模型检验表

序号

年份

原始值

预测值

残差

相对误差

级比偏差

1

2013

14.6

14.8

0.0057

0.37%

0.0203

2

2014

14.68

14.8

0.1638

0.54%

0.0107

3

2015

14.73

14.9

0.3290

0.39%

0.0232

4

2016

14.8

14.9

0.4984

0.47%0.

0.0341

5

2017

14.75

14.9

0.2699

0.65%

0.0425

6

2018

14.96

15.0

0.0378

0.09%

0.0018

7

2019

14.98

15.0

0.2140

0.09%

0.0017

8

2020

14.9

15.0

0.1423

0.09%

0.0018

9

2021

14.85

15.0

0.1470

0.35%

0.0742

10

2022

14.91

15.1

0.6241

0.18%

0.0023

2.3.2 GM(1,1)模型预测结果分析

    通过建立的GM(1,1)模型分别预测得到2050年和2100年全球平均气温为15.90℃、17.50℃，具体结果见代码模块。

灰色预测模型代码

import matplotlib.pyplot as plt

import pandas as pd

import numpy as np

def GM11(x,n):

    x1 = x.cumsum()#一次累加 

    z1 = (x1[:len(x1) - 1] + x1[1:])/2.0#紧邻均值 

    z1 = z1.reshape((len(z1),1)) 

    B = np.append(-z1,np.ones_like(z1),axis=1) 

    Y = x[1:].reshape((len(x) - 1,1))

    #a为发展系数 b为灰色作用量

    [[a],[b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y)#计算待估参数 

    result = (x[0]-b/a)*np.exp(-a*(n-1))-(x[0]-b/a)*np.exp(-a*(n-2))  #预测方程

    S1_2 = x.var()#原序列方差

    e = list()#残差序列

    for index in range(1,x.shape[0]+1):

        predict = (x[0]-b/a)*np.exp(-a*(index-1))-(x[0]-b/a)*np.exp(-a*(index-2))

        e.append(x[index-1]-predict)

        print(predict)    #预测值

    S2_2 = np.array(e).var()#残差方差

    C = S2_2/S1_2#后验差比

    if C<=0.35:

        assess = '后验差比<=0.35，模型精度等级为好'

    elif C<=0.5:

        assess = '后验差比<=0.5，模型精度等级为合格'

    elif C<=0.65:

        assess = '后验差比<=0.65，模型精度等级为勉强'

    else:

        assess = '后验差比>0.65，模型精度等级为不合格'

    #预测数据

    predict = list()

    for index in range(x.shape[0]+1,x.shape[0]+n+1):

        predict.append((x[0]-b/a)*np.exp(-a*(index-1))-(x[0]-b/a)*np.exp(-a*(index-2)))

        #print((x[0]-b/a)*np.exp(-a*(index-1)))

        #print((x[0]-b/a)*np.exp(-a*(index-2)))

    predict = np.array(predict)

    return

            'a':'value':a,'desc':'发展系数',

            'b':'value':b,'desc':'灰色作用量',

            'predict':'value':result,'desc':'第%d个预测值'%n,

            'C':'value':C,'desc':assess,

            'predict':'value':predict,'desc':'往后预测%d个的序列'%(n),

           

if __name__ == "__main__":

    data = np.array([14.6,14.68,14.73,14.8,14.75,14.96,14.98,14.9,14.85,14.91])

    x = data[0:5]#数据

    y = data[0:]#预测数据

    result = GM11(x,38)

    predict = result['predict']['value']

    predict = np.round(predict,1)

    print('真实值:',y)

    print('预测值:',predict)

    print(result)

plt.plot( data, color='r', linestyle="-", marker='*', label='True')

plt.plot(predict, color='b', linestyle="--", marker='.', label="Predict")

plt.legend(loc='upper right')

plt.xlabel('xlabel')

plt.ylabel('ylabel')

plt.title('Prediction by Grey Model (GM(1,1))')

plt.show()

#利用GM(1,1)模型预测2050年全球平均温度结果：

（14.670223149836602

14.69807920745643

14.725988158610562

14.753950103731768

14.78196514345018

真实值: [14.6  14.68 14.73 14.8  14.75 14.96 14.98 14.9  14.85 14.91]

预测值: [14.8 14.8 14.9 14.9 14.9 15.  15.  15.  15.  15.1 15.1 15.1 15.2 15.2

 15.2 15.2 15.3 15.3 15.3 15.4 15.4 15.4 15.4 15.5 15.5 15.5 15.6 15.6

 15.6 15.6 15.7 15.7 15.7 15.8 15.8 15.8 15.9 15.9]

'a': 'value': -0.0018970157440081903, 'desc': '发展系数', 'b': 'value': 14.656445941555171, 'desc': '灰色作用量', 'predict': 'value': array([14.81003338, 14.83815491, 14.86632984, 14.89455827, 14.9228403 ,

       14.95117603, 14.97956556, 15.008009  , 15.03650646, 15.06505802,

       15.09366379, 15.12232389, 15.1510384 , 15.17980744, 15.2086311 ,

       15.2375095 , 15.26644273, 15.2954309 , 15.32447411, 15.35357247,

       15.38272608, 15.41193505, 15.44119949, 15.47051948, 15.49989516,

       15.52932661, 15.55881395, 15.58835728, 15.6179567 , 15.64761233,

       15.67732427, 15.70709263, 15.73691751, 15.76679903, 15.79673728,

       15.82673238, 15.85678444, 15.88689356]), 'desc': '往后预测38个的序列', 'C': 'value': 0.32196000409798153, 'desc': '后验差比<=0.35，模型精度等级为好'）

#利用GM(1,1)模型预测2100年全球平均温度结果：

14.670223149836602

14.69807920745643

14.725988158610562

14.753950103731768

14.78196514345018

真实值: [14.6  14.68 14.73 14.8  14.75 14.96 14.98 14.9  14.85 14.91]

预测值: [14.8 14.8 14.9 14.9 14.9 15.  15.  15.  15.  15.1 15.1 15.1 15.2 15.2

 15.2 15.2 15.3 15.3 15.3 15.4 15.4 15.4 15.4 15.5 15.5 15.5 15.6 15.6

 15.6 15.6 15.7 15.7 15.7 15.8 15.8 15.8 15.9 15.9 15.9 15.9 16.  16.

 16.  16.1 16.1 16.1 16.2 16.2 16.2 16.3 16.3 16.3 16.3 16.4 16.4 16.4

 16.5 16.5 16.5 16.6 16.6 16.6 16.7 16.7 16.7 16.8 16.8 16.8 16.8 16.9

 16.9 16.9 17.  17.  17.  17.1 17.1 17.1 17.2 17.2 17.2 17.3 17.3 17.3

 17.4 17.4 17.4 17.5]

'a': 'value': -0.0018970157440081903, 'desc': '发展系数', 'b': 'value': 14.656445941555171, 'desc': '灰色作用量', 'predict': 'value': array([14.81003338, 14.83815491, 14.86632984, 14.89455827, 14.9228403 ,

       14.95117603, 14.97956556, 15.008009  , 15.03650646, 15.06505802,

       15.09366379, 15.12232389, 15.1510384 , 15.17980744, 15.2086311 ,

       15.2375095 , 15.26644273, 15.2954309 , 15.32447411, 15.35357247,

       15.38272608, 15.41193505, 15.44119949, 15.47051948, 15.49989516,

       15.52932661, 15.55881395, 15.58835728, 15.6179567 , 15.64761233,

       15.67732427, 15.70709263, 15.73691751, 15.76679903, 15.79673728,

       15.82673238, 15.85678444, 15.88689356, 15.91705985, 15.94728342,

       15.97756438, 16.00790284, 16.0382989 , 16.06875268, 16.09926429,

       16.12983384, 16.16046143, 16.19114717, 16.22189119, 16.25269358,

       16.28355445, 16.31447393, 16.34545212, 16.37648913, 16.40758507,

       16.43874006, 16.46995421, 16.50122762, 16.53256042, 16.56395271,

       16.59540462, 16.62691624, 16.6584877 , 16.6901191 , 16.72181057,

       16.75356222, 16.78537415, 16.81724649, 16.84917936, 16.88117285,

       16.91322709, 16.9453422 , 16.9775183 , 17.00975548, 17.04205388,

       17.07441361, 17.10683478, 17.13931752, 17.17186193, 17.20446814,

       17.23713627, 17.26986642, 17.30265872, 17.33551329, 17.36843025,

       17.4014097 , 17.43445178, 17.4675566 ]), 'desc': '往后预测88个的序列', 'C': 'value': 0.32196000409798153, 'desc': '后验差比<=0.35，模型精度等级为好'

 2.4 BP神经网络模型预测

2.4.1 BP神经网络训练

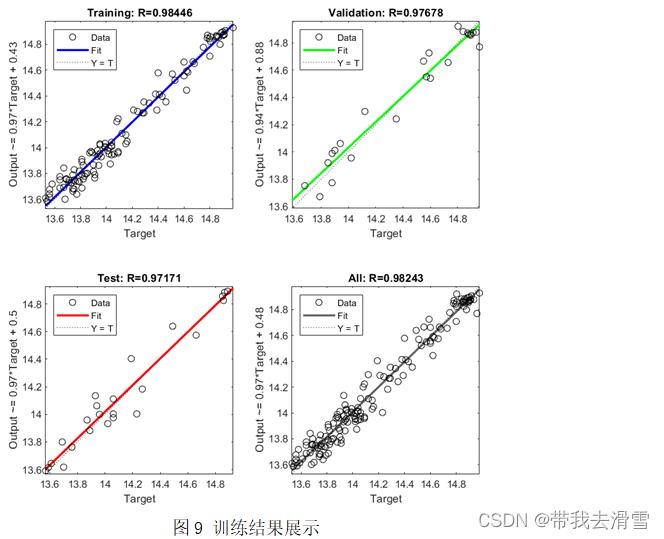
       将全球平均气温数据进行数据预处理后得到138个样本，选取120个作为训练集，18个作为测试集进行BP神经网络训练。训练表现和训练结果分别见图8、图9，根据得到的结果，判断是否满足需求，一般是模型的MSE值越小，R值越接近1。结合图像可以看出，BP神经网络的训练结果较好，可以进行预测。

        利用BP神经网络进行预测，其预测结果见表2，从表中可以看出2050年全球平均温度的预测值为14.89℃，2100年全球平均温度的预测为15.55℃，二者均未达到20℃。

表2 BP神经网络预测值

Year

temperature℃

Year

temperature℃

Year

temperature℃

Year

temperature℃

2023

14.80

2051

14.87

2100

15.55

2196

18.45

2024

14.78

2052

14.89

2101

15.68

2197

18.49

2025

14.80

2053

14.89

2102

15.7

2198

18.5

2026

14.76

2054

14.88

2103

15.79

2199

18.48

2027

14.83

2055

14.93

2104

15.99

2200

18.55

2028

14.88

2056

14.94

2105

15.84

2201

18.6

2029

14.90

2057

14.95

2106

15.98

2202

18.65

2030

14.85

2058

14.91

2107

16.12

2203

18.59

2031

14.87

2059

14.95

2108

16.04

2204

18.64

2032

14.84

2060

14.95

2109

16.21

2205

18.69

2033

14.80

2061

14.96

2110

16.37

2206

18.75

2034

14.80

2062

14.95

2111

16.31

2207

18.79

2035

14.78

2063

14.96

2112

16.45

2208

18.86

2036

14.86

2064

14.96

2113

16.35

2209

18.74

2037

14.78

2065

14.97

2114

16.68

⋮

⋮

⋮

⋮

⋮

⋮

⋮

⋮

2267

19.97

2050

14.89

2099

15.52

2195

18.37

2268

20.03

BP神经网络模型代码

close all

clc

input=a;

output=b;

input_train = input(1:120,:)';

output_train =output(1:120,:)';

input_test = input(121:138)';

output_test =output(121:138,:)';

inputnum=2; % 输入层节点数量

hiddennum=5;% 隐含层节点数量

outputnum=1; % 输出层节点数量

 [inputn,inputps]=mapminmax(input_train);%归一化到[-1,1]之间，inputps用来作下一次同样的归一化

[outputn,outputps]=mapminmax(output_train);

net=newff(inputn,outputn,hiddennum,'tansig','purelin','trainlm'); W1= net. iw1, 1;

B1 = net.b1;

W2 = net.lw2,1;

B2 = net. b2;

net.trainParam.epochs=1000;    % 训练次数，这里设置为1000次

net.trainParam.lr=0.01;         % 学习速率，这里设置为0.01

net.trainParam.goal=0.00001;    % 训练目标最小误差，这里设置为0.00001

net=train(net,inputn,outputn);

inputn_test=mapminmax('apply',input_test,inputps);

an=sim(net,inputn_test);

test_simu=mapminmax('reverse',an,outputps);

error=test_simu-output_test;

figure('units','normalized','position',[0.119 0.2 0.38 0.5])

plot(output_test,'bo-','markersize',10,'markerfacecolor','b')

hold on

plot(test_simu,'rs-','markersize',10,'markerfacecolor','r')

grid on%添加网格

legend('期望值','预测值','误差')

xlabel('数据组数')

ylabel('样本值')

title('BP神经网络测试集的预测值')

[c,l]=size(output_test);

MAE1=sum(abs(error))/l;

MSE1=error*error'/l;

RMSE1=MSE1^(1/2);

disp(['-----------------------误差计算--------------------------'])

disp(['隐含层节点数为',num2str(hiddennum),'时的误差结果如下：'])

disp(['平均绝对误差MAE为：',num2str(MAE1)])

disp(['均方误差MSE为：       ',num2str(MSE1)])

disp(['均方根误差RMSE为：  ',num2str(RMSE1)])

 3 三种模型预测比较

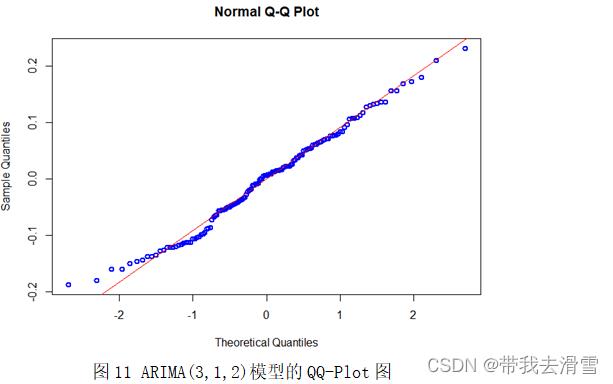
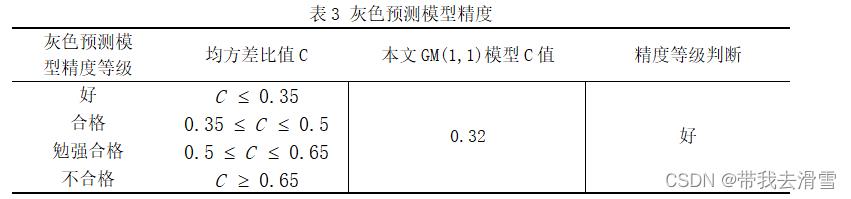
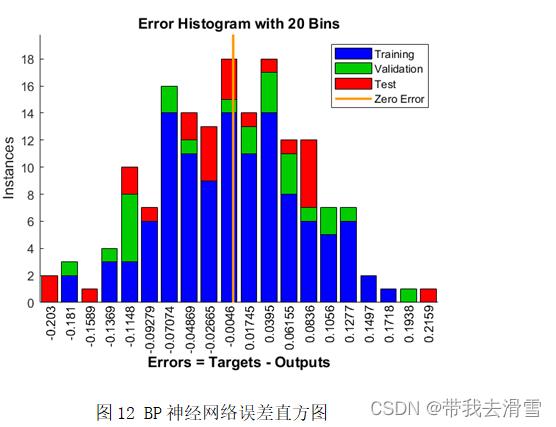
        ARIMA自回归预测模型的预测效果可以通过残差分布来确定，良好的ARIMA自回归预测模型的残差应满足均值为零的正态分布，即QQ-Plot图像近似为过原点的一条直线，则残差服从正态分布且均值为零。通过图11可以看出ARIMA(3,1,2)模型的预测效果较好，但在首尾两端仍有部分点未落在直线上。通过表3可以看出GM（1，1）模型的预测精度也较好，但由于灰色预测只用了原始数据的很小一部分数据进行预测，预测效果不如另外两个模型精准。通过图12，我们可以看出BP神经网络的误差直方图基本服从正态分布，预测效果较好。因此，经过对比，认为BP神经网络的预测效果最佳。 

   

 需要数据集的家人们可以去百度网盘（永久有效）获取：

链接：https://pan.baidu.com/s/1NcsNDS_BCt2IGgeKbu069A?pwd=2138 
提取码：2138 

更多优质内容持续发布中，请移步主页查看。

   点赞+关注,下次不迷路！

以上是关于运用自回归滑动平均模型灰色预测模型BP神经网络三种模型分别预测全球平均气温，并进行预测精度对比（附代码数据）的主要内容，如果未能解决你的问题，请参考以下文章

BP回归预测基于matlab思维进化算法优化BP神经网络回归预测含Matlab源码 2031期

预测模型基于麻雀算法改进广义回归神经网络(GRNN)实现数据预测matlab代码

基于集成回声状态网络模型在兰州市艾滋病发病例数预测中的应用

时间序列模式——ARIMA模型

随机序列模型

BP回归预测Logistic混沌映射改进的麻雀算法优化BP神经网络回归预测含Matlab源码 1552期