CSP 202104-4 校门外的树 python 动态规划DP + 约数优化

Posted 2022-06-04 风信子的猫Redamancy

tags:

篇首语：本文由小常识网(cha138.com)小编为大家整理，主要介绍了CSP 202104-4 校门外的树 python 动态规划DP + 约数优化相关的知识，希望对你有一定的参考价值。

CSP 202104-4 校门外的树 python 动态规划DP + 约数优化

题目描述

X 校最近打算美化一下校园环境。前段时间因为修地铁，X 校大门外种的行道树全部都被移走了。现在 X 校打算重新再种一些树，为校园增添一抹绿意。

X 校大门外的道路是东西走向的，我们可以将其看成一条数轴。在这条数轴上有 n 个障碍物，例如电线杆之类的。虽然障碍物会影响树的生长，但是障碍物不一定能被随便移走，所以 X 校规定在障碍物的位置上不能种树。n 个障碍物的坐标都是整数；如果规定向东为正方向，则 n 个障碍物的坐标按照从西到东的顺序分别为 a1,a2,⋯,an。X 校打算在 [a1,an] 之间种一些树，使得这些树看起来比较美观。

X 校希望，在一定范围内，树应该是等间隔的。更具体地说，如果把 [a1,an) 划分成一些区间 [ap1,ap2),⋯,[apm−1,apm)（1=p1<p2<⋯<pm=n），那么每个区间 [api,api+1) 内需要至少种一棵树，且该区间内种的树的坐标连同区间端点 api,api+1 应该构成一个等差数列。不同区间的公差，也就是树的间隔可以不相同。

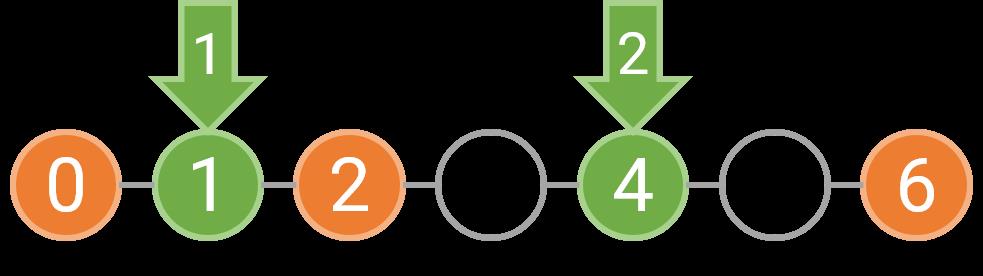
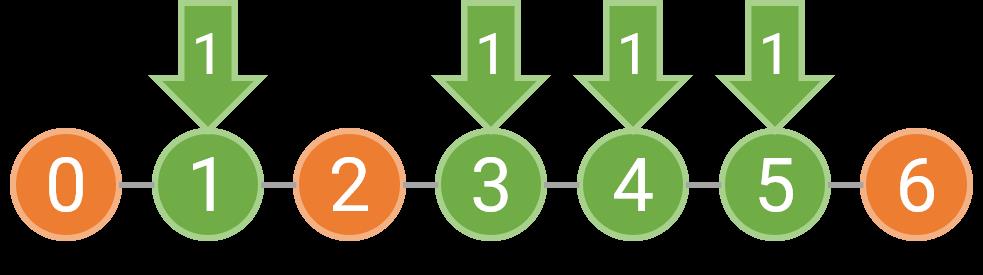
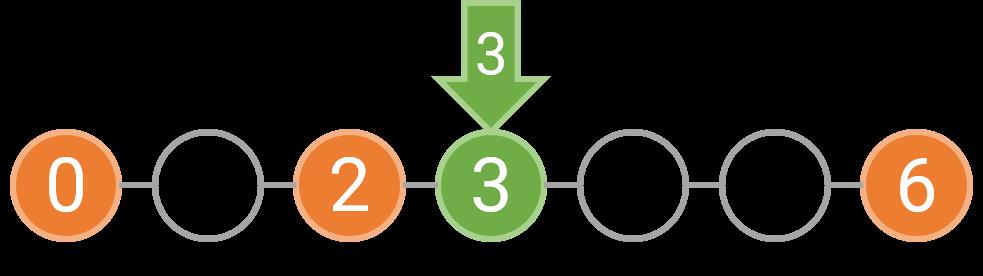
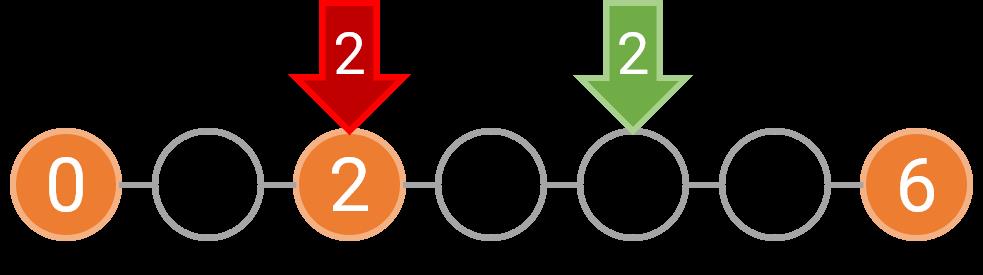
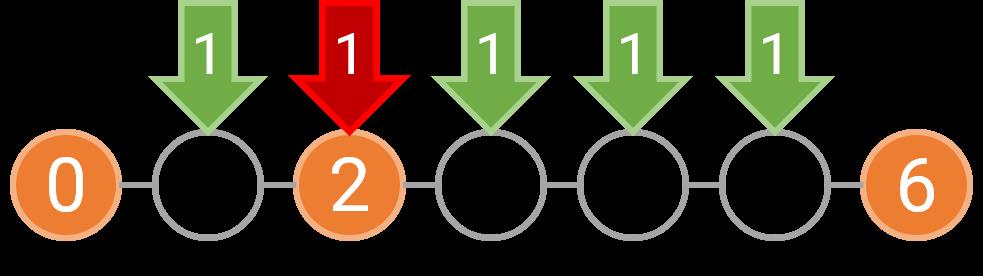
例如，如果障碍物位于 0,2,6 这三处，那么我们可以选择在 [0,2) 和 [2,6) 分别种树，也可以选择在 [0,6) 等间隔种树。如果是分别在 [0,2) 和 [2,6) 种树，由于每个区间内至少要种一棵树，坐标 1 上必须种树；而 [2,6) 上的树可以按照 1 的间隔种下，也可以按照 2 的间隔种下。下图表示了这两种美观的种树方案，其中橙色的圆表示障碍物，绿色的圆表示需要在这个位置种树，箭头上的数字表示种下这棵树时对应的间隔为多少。

对区间 [0,2) 和 [2,6) 分别以 1 和 2 的间隔种树是美观的

对区间 [0, 2) 和 [2, 6) 分别以 1 的间隔种树也是美观的而如果选择在 [0,6) 区间等间隔种树，我们只能以 3 的间隔种树，因为无论是选择间隔 1 或者间隔 2，都需要在坐标 2 上种树，而这个位置已经有障碍物了。下图分别表示了间隔为 3,2,1 时的种树情况，红色箭头表示不能在这里种树。

对区间 [0, 6) 以 3 的间隔种树是美观的

图 4: 对区间 [0, 6) 以 2 的间隔种树是不美观的

图 5: 对区间 [0, 6) 以 1 的间隔种树也是不美观的

一般地，给定一个区间 [al,ar)，对于树的坐标的集合 T⊂(al,ar)（T⊂Z），归纳定义 T 在 [al,ar) 上是美观的：

如果 T≠∅，T∩al,al+1,⋯,ar=∅，并且存在一个公差 d≥1，使得 T∪al,ar 中的元素按照从小到大的顺序排序后，可以构成一个公差为 d 的等差数列（显然，这个等差数列的首项为 al，末项为 ar），则 T 在 [al,ar) 上是美观的；
如果 T∩al,al+1,⋯,ar=∅，并且存在一个下标 m（l<m<r），使得 T∩(al,am) 在 [al,am) 上是美观的，且 T∩(am,ar) 在 [am,ar) 上是美观的，则 T 在 [al,ar) 上是美观的。

根据这一定义，空集在任意区间上都不是美观的；另外，如果存在下标 i 使得 ai∈T，那么 T 一定不是美观的。
我们称两种种树的方案是本质不同的，当且仅当两种方案中，种树的坐标集合不同。请帮助 X 校对 [a1,an) 求出所有本质不同的美观的种树方案。当然，由于方案可能很多，你只需要输出总方案数对 10^9+7 取模的结果。

输出格式

输出到标准输出。
输出一个非负整数，表示本质不同的美观的种树方案的数量对 109+7 取模的结果。

样例输入1

3
0 2 6

样例输出1

样例说明1

这组样例即为题面描述中提到的那组。

样例输入2

11
0 10 20 30 40 50 60 70 80 90 100

样例输出2

样例输入3

333
33 44 67 210 528 762 873 984 1234 1466 1739 2859 3421 4061 4598 5172 5201 5220 5261 5322 5389 5559 6670 7070 7898 8079 8129 8192 8616 8641 8806 9559 9585 9750 10263 10627 10674 10692 10903 11649 11885 12179 12307 12743 13173 13352 13389 13496 13611 15292 15321 16018 16327 16415 16959 16972 17499 17617 17786 18476 18966 19239 19498 19875 20312 20392 21603 21620 21730 21967 21972 21999 22015 22590 22775 23709 23839 24165 24408 24595 25160 25479 25812 26482 27328 28101 28297 28305 28342 28557 28986 29110 29401 29765 30292 30493 30739 31027 31201 31218 31414 32089 32759 32770 32777 32815 32877 32890 33297 33457 33603 33757 33866 34498 34525 34659 34679 34861 34870 34997 35311 35846 36411 36457 36738 36902 37940 38228 40156 40320 40705 40737 40803 41066 41443 41460 41954 41968 42040 42062 42099 43281 43320 43527 43537 43587 43729 44750 44822 45655 45769 46109 46525 47060 47128 47999 48635 48887 48981 49366 49424 49524 50546 50580 50689 51332 51861 51943 52097 52702 53009 53067 53397 53526 53901 54280 54399 54801 55535 55592 55740 55843 56110 56428 56552 56682 56848 57179 57688 57797 57847 57959 58330 58831 59553 59699 59884 59939 61233 61636 61732 61908 62145 62549 62649 62740 62912 62971 63053 64312 64322 64412 64816 64845 64873 64923 64976 65023 65166 65496 66065 66491 66803 66941 67081 68331 68336 68360 68476 69179 69719 69758 69948 70072 70544 70598 70990 71014 71454 71687 71743 71958 72282 72384 72456 72985 73327 74325 75046 75097 76647 77062 77088 77431 77553 77673 77753 78217 78518 78564 79565 79588 79686 80275 80939 81052 81348 81386 81440 81589 81610 81793 82408 82801 82836 83239 83466 83610 83867 83943 84441 84467 85248 85305 85554 85565 85758 86251 86603 86743 87323 87565 87824 87833 88265 88309 89178 89509 89618 89699 89708 90331 90359 90878 90902 91449 92284 92374 92549 92609 93609 94345 94934 95140 95475 95733 95985 95995 96270 96641 96807 97003 97632 98160 98677 98853 98943 99037 99055 99075 99185 99395 99592

样例输出3

思路

这道题需要用到动态规划DP，并且f[0]=1

设 $f [i]$ 为前i个障碍物所能生成的最多可能性
设 $c n t [i] [j]$ 为从第i个障碍物到第j个障碍物的可行方案数
想要求 $c n t [i] [j]$ 只需从位置i枚举所有间隔的可能性, 看是否能在不触碰到 i , j 之间的障碍物的情况下到达

我们就可以写出我们的动态转移方程
$\\sum_j=0^i-1 f[j]*cnt(j,i)$
比如我们求f[2]的时候，就是
$\\\\ f[2] = f[1]*cnt(1,2) + f[0]*cnt(0,2)$

动态规划的话只能够拿到60分，但是如果要拿满分，还需要进行约数优化的方法。

除此之外，得到我们的cnt数组的时候，第j个障碍物到第i个障碍物之间的方案数，注意这里是把a[j]和a[i]之间看作一个整体进行植树，不考虑分割情况，即在此区间里所有的树和a[j]、a[i]构成等差数列。如果只是穷举的话，我们就会超时，所以这里需要进行约数优化的方法。

约数优化：可以想到第j个障碍物到第i个障碍物之间植树间隔必须为 $a [i] - a [j]$ 的因子，方案数一定小于等于因子个数，因为这个间隔还不能撞上 $a [j]$ 和 $a [i]$ 之间的障碍物。我们倒着从 $i - 1$ 开始枚举 $j$ ，这样一开始$ i - 1$ 和 $i $之间是没有障碍物的，则$ a[i] - a[i - 1 $] 的所有因子都满足条件；然后到了$ i - 2 $，同样先枚举$ a[i] - a[i - 2] $的所有因子，这些因子中已经处于集合中的一定不可，等于$ a[i]-a[i-1] $的也不可，因为按这样的间隔排列一定会有树遇上$ a[i - 1] $这个障碍物；以此类推，倒着枚举到$ a[i] - a[k] $因子的时候，如果已经在之前的枚举中使用过，则跳过，否则方案数就加一。我们使用一个状态数组$ st[M]$，保存某个因子是否已经使用过了,。

代码

60分运行超时

第一个方法代码只能过60%，得到60分就运行超时了

# http://118.190.20.162/view.page?gpid=T125

n = int(input())
a = list(map(int,input().split()))
N = 1010
MOD = int(1e9+7)

def get_cnt(a,b):
    res = 0
    maxn = b - a
    for i in range(1,maxn+1): # 枚举间隔
        if a + i == b: continue
        for j in range(a+i,b+1,i): # 不断进行枚举
            if j > b: # 没有到达b
                break
            if j == b:
                res += 1
                break
            if st[j]:
                break
    return res

'''
设f[i]为前i个障碍物所能生成的最多可能性
设 cnt[i][j]为从第i个障碍物到第j个障碍物的可行方案数
想要求cnt[i][j]只需从位置i枚举所有间隔的可能性,看是否能在不触碰到i,j之间的障碍物的情况下到达
'''
f = [0]*N
f[0] = 1
cnt = [[0]*N for _ in range(N)]

from collections import defaultdict
st = defaultdict(int)
for i in range(n):
    st[a[i]] = 1

for i in range(n-1):
    for j in range(i+1,n):
        cnt[i][j] = get_cnt(a[i],a[j])%MOD
        

for i in range(1,n):
    for j in range(0,i):
        f[i] = (f[i] + f[j]*cnt[j][i]%MOD)%MOD

print(f[n-1])

动态规划DP + 约数优化

# http://118.190.20.162/view.page?gpid=T125
from collections import defaultdict

n = int(input())
a = list(map(int,input().split()))
N = 1010
MOD = int(1e9+7)
'''
设f[i]为前i个障碍物所能生成的最多可能性
设 cnt[i][j]为从第i个障碍物到第j个障碍物的可行方案数
想要求cnt[i][j]只需从位置i枚举所有间隔的可能性,看是否能在不触碰到i,j之间的障碍物的情况下到达
'''

f = [0]*N
f[0] = 1

q = defaultdict(list)
M = 100010
for i in range(1,M):
    for j in range(2*i,M,i):
        q[j].append(i)

# 动态规划
for i in range(1,n): # 每轮添加一个障碍物，计算添加后的方案总数
    st = defaultdict(int) # 清空状态数组
    for j in range(i-1,-1,-1):
        d = a[i] - a[j]
        cnt = 0
        for k in q[d]: # 枚举d的所有的因子，也就是所有可能的方案
            if not st[k]: # 如果此因子之前没使用过，方案数加一，并标记当前因子已被用过
                cnt += 1
                st[k] = 1
        # 手动添加d本身，因为下一轮如果按照这个间隔植树就会撞上本轮添加的障碍物
        st[d] = 1 # 因为最后一个障碍物必选
        f[i] = (f[i] + f[j]*cnt)%MOD
        
print(f[n-1])