计量经济学 学习笔记（长篇 未完成）

Posted 2022-03-14 好奇小圈

文章目录

• 前言
• 一、基本模型
• • 1、一元线性回归模型
  • 2、多元线性回归模型
  • 3、可线性化的非线性模型
• 二、数据特征
• • 1、处理异方差
  • 2、自相关
  • 3、多重共线性
  • 4、虚拟变量的应用
  • 5、F,LR,Wald,JB检验
• 三、面板数据类型
• • 1、混合模型
  • 2、固定效应模型
  • 3、随机效应模型
• 四、其他
• 总结

---

前言

2021年暑假自学的内容，现由纸质笔记整理到CSDN上。

---

一、基本模型

1、一元线性回归模型

回归线的定义

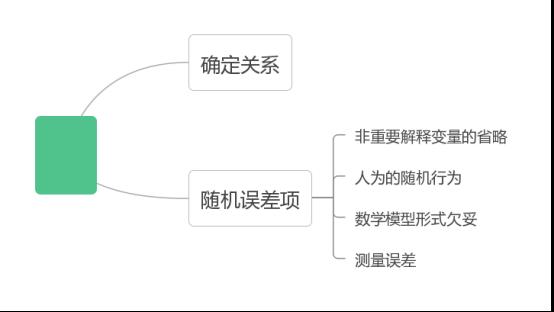
回归线的基本假定
关于模型关系的假设：模型设定正确假设、线性回归假设；
关于解释变量的假设：确定性假设、与随机项不相关假设、观测值变化假设、无完全共线性假设、样本方差假设（随着样本容量的无限增加。解释变量x的样本方差趋于一有限常数，时间序列）；
关于随机项的假设：0均值假设
$$E\left({\mu }_i\mid X_i\right)=0,i=1,2,\cdots ,n$$
同方差假设
$$\mathrm{Var}\left({\mu }_i\mid X_i\right)={\sigma }^2,i=1,2,\cdots ,n$$
序列不相关假设
$$\mathrm{Cov}\left({\mu }_i,{\mu }_j\mid X_i,X_j\right)=0,i,j=1,2,\cdots ,n,i\ne j$$；
随机项的正态性假设：正态性假设
$${\mu }_i\sim N\left(0,{\sigma }^2\right)\to {\mu }_i\sim \mathrm{NID}\left(0,{\sigma }^2\right)$$
平方和
$$\widehat{y_i}=\widehat{Y_i}-\overline{Y_i}$$
$$\sum y_i^2=\sum {\widehat{y_i}}^2+\sum {\widehat{u_i}}^2$$
$$\widehat{u_i}=\widehat{U_i}$$
总平方和（波动程度）TSS：
$$\sum y_i^2$$
解释平方和ESS：
$$\sum {\widehat{y_i}}^2$$
残差平方和RSS（$y_i$的波动，没有被$x_i$解释的部分）：
$$\sum {\widehat{u_i}}^2$$

拟合优度定义及含义
可决系数$R^2$：被解释变量的波动程度，由解释变量解释的那一部分
$$R^2=ESS/TSS=1-RSS/TSS$$
相关性r：常见的有斯皮尔曼相关性（不要求正态分布）、皮尔逊相关性（要求正态分布）

随机干扰项方差的置信区间
$\frac{(n-2){\hat{\delta }}^2}{{\delta }^2}$服从卡方分布，其中${\delta }^2$置信区间为$\frac{(n-2){\hat{\delta }}^2}{x_{a/2}^2},\frac{(n-2){\hat{\delta }}^2}{x_{1-a/2}^2}]$
假设检验略

均值预测和个体预测
个体预测： x 0