51nod 1102 面积最大的矩形 && 新疆大学OJ 1387: B.HUAWEI's billboard 单调栈+拼凑段（o(n) 或 o（nlog(n)）

Posted 2020-11-18 zhangjiuding

题面1：

?

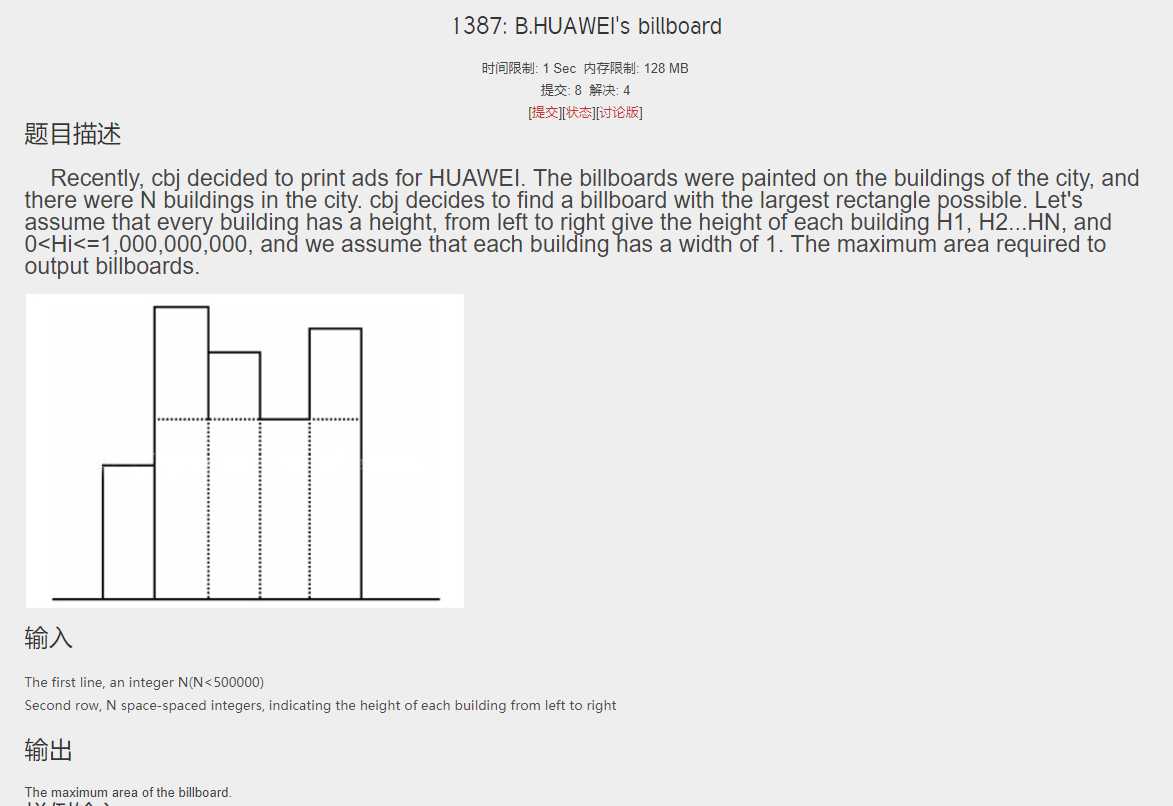
题面2：

?

两道题除了数据范围不同，没有任何差异，两道题都可以o(n)（单调栈），o(nlog(n))（我自己的做法）解决。

解题思路1：（单调栈）

1. 对于每个点找到右边第一个比它小的位置con1，并且找到左边第一个比它小的位置con2。
2. 对于每个点更新答案为ans = max(ans, (con2-con1-1)*value[i])。
3. 1的做法是两次裸的单调栈，时间复杂度为o(n)。

代码1：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//在新疆大学OJ提交需要将此处三个数组改为500010，否则会运行超时
ll a[50010];
int l[50010],r[50010];
int main(){
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    ll ans = 0;
    for(int i = 1;i <= n; ++i){
        cin >> a[i];
    }
    a[0] = a[n+1] = -1;
    stack<int> s;
    s.push(1);
    for(int i = 2;i <= n+1; ++i){
        while(s.size() and a[i] < a[s.top()]){
            r[s.top()] = i;
            s.pop();
        }
        s.push(i);
    }
    while(s.size()) s.pop();
    s.push(n);
    for(int i = n-1;i >= 0; --i){
        while(s.size() and a[i] < a[s.top()]){
            l[s.top()] = i;
            s.pop();
        }
        s.push(i);
    }
    for(int i = 1;i <= n; ++i){
        ans = max(ans, (a[i]*(r[i]-l[i]-1)));
    }
    cout << ans << endl;
    return 0;
}

解题思路2：（拼凑段）

1. 这是我自己瞎搞的写法，不知道算什么方法，不过大家可以看一看思路，可能什么时候就能用到了。
2. 首先，记下输入的数字的位置，然后对这个结构体按数字从打到小排序。

3. 遍历这个结构体数组（这时数字是从大到下的），段（一个结构体，有l,r,used三个成员变量，l指这个段的左端位置，r指这个段的右端位置）

   a. 若这个数字的原位置的左右边两个数字都已形成段，则将这两段拼成一段，具体做法是将左边段的r延长至右端，当前数字为这一段的最小值，更新ans。 b. 若这个数字的原位置的左边形成段，右边没有形成段，则把这个数字加入到左边的段，当前数字为这一段的最小值，更新ans。 c. 若这个数字的原位置的右边形成段，左边没有形成段，则把这个数字加入到右边的段，当前位置为这一段的最小值，更新ans。

   d. 若这个数字的原位置的左边和右边都没有形成段，则把这个数字加入到一个新的段，新的段的l和r都等于这个数字的原先位置,更新ans。

4. 可能会想到查找左边位置所处的段和右边所处的段需要o(n)处理起来会变成o(n^2)，这时候我们加一个索引数组index,index[i]表示位置为i的数字所处的段。
5. 可能还会想到更新index需要花费o(n),处理起来会变成o(n^2)，但是仔细想想我们会发现不需要更新这个段所有的index，只用更新index[l]和index[r]，因为中间的在后面将不会用到。
6. 这样算下来排序的时间复杂度是o(nlogn)，处理的时间是o(n)，总时间复杂度就是o(nlogn)。

7. 可能还有人问为什么正确？排序之后先插入大的，后插入小的，会发现当前插入的这个点一定是这个点的最优情况。

代码2:

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
//在新疆大学OJ提交需要将此处的50010全部改为500010 

//输入的数组，val为这个点的数字，idx表示原下标。 
struct node{
    ll val;
    int idx;
}a[50010];
//段，l表示左端，r表示右端 ，k表示段的个数。 
struct segment{
    int l;int r;
}seg[50010];
int k = 1;
//index[i]表示第i个位置数字所处的段。 
int index[50010];

int n;
bool cmp(node x,node y){
    return x.val > y.val;
}

int main(){
    ios::sync_with_stdio(false);
    int n;
    cin >> n;
    ll ans = 0;
    for(int i = 1;i <= n; ++i){
        cin >> a[i].val;
        a[i].idx = i;
        ans = max(ans , a[i].val);
    }
    sort(a+1, a+1+n, cmp);
    for(int i = 1;i <= n; ++i){
        int idxl = index[a[i].idx-1];
        int idxr = index[a[i].idx+1];
        if(idxl != 0 and idxr != 0){    //左右边都形成一段。 
            seg[idxl].r = seg[idxr].r;
            index[seg[idxr].r] = idxl;
            ans = max(ans, a[i].val*(seg[idxl].r-seg[idxl].l+1));
        }else if(idxl != 0 and idxr == 0){  //左边形成段，右边未形成。 
            seg[idxl].r++;
            index[a[i].idx] = idxl;
            ans = max(ans, a[i].val*(seg[idxl].r-seg[idxl].l+1));
        }else if(idxl == 0 and idxr != 0){  //右边形成段，左边未形成。 
            seg[idxr].l--;
            index[a[i].idx] = idxr;
            ans = max(ans, a[i].val*(seg[idxr].r-seg[idxr].l+1));
        }else if(idxl == 0 and idxr == 0){  //左右边均未形成段。 
            seg[k].l = a[i].idx;
            seg[k].r = a[i].idx;
            index[a[i].idx] = k; 
            k++;
        }
    }
    cout << ans << endl;
    return 0;
}