蛙跳算法怎么计算各个青蛙的适应值

Posted 2023-04-09

参考技术A 　　对于青蛙群体，具有全局最好适应度的解表示为U g；对于每一个子族群，具有最好适应度的解表示为UB，最差适应度的解表示为UW。首先对每个子族群进行局部搜索，即对子族群中最差适应度的青蛙个体进行更新操作，更新策略为
　　青蛙更新距离 Ds=rand()*(Pb-Pw) （1）
　　更新后的青蛙 newDw=oldPw+Ds（-Dmax≦Ds≦Dmax） （2）
　　其中， Ds 表示青蛙个体的调整矢量， Dmax表示青蛙个体允许改变的最大步长。如设Uw=[1 3 5 4 2],UB=[2 1 5 3 4],允许改变的最大步长Dmax =3，若rand=0.5 ，则U q(1) =1+minint[0.5 × (2−1)],3=1;U q(2) =3+maxint[0.5×(1−3)], −3=2;依此相同的操作完成更新策略后可得到一个新解U q=[1 2 5 4 3].本回答被提问者和网友采纳

BP回归预测基于matlab随机蛙跳算法SFLA优化神经网络数据回归预测含Matlab源码 2272期

⛄一、蛙跳算法

1 改进的免疫蛙跳算法
免疫蛙跳算法具有混合蛙跳算法的全局优化与局部细致搜索优点, 可以优化连续问题和离散问题, 具有较强的鲁棒性;同时, 群体具有的免疫机制对群体进行控制和调节, 把目标函数和制约条件作为青蛙群体的抗原, 保证生成的青蛙群体直接与问题相关联, 收敛方向得以控制;对与抗原亲和力高的青蛙抗体进行记忆, 并从中提取免疫疫苗对抗体群进行注射, 保证抗体群在更新过程中的多样性, 提高算法的效率, 防止群体的退化。参照免疫算法和混合蛙跳算法的设计原理, 下面给出具体实现步骤:

1. 步骤1:抗原输入。输入目标函数和各种约束作为免疫蛙跳算法的抗原。

2. 步骤2:针对F只青蛙 (解) , 产生初始群体。生成初始抗体群N、促进记忆青蛙群N1、检测记忆青蛙群N2。
   
   式中:Tact为一个预先确定的亲和力阈值。

3. 步骤4:免疫记忆青蛙群体更新。根据一定比例, 从青蛙抗体群N中选出亲和力高的抗体, 用它们替换促进记忆青蛙群体N1中亲和力低的抗体;将抗体群N中亲和力低的抗体选入检测记忆青蛙群体N2, 用它们替换检测记忆青蛙群体N2中亲和力高的抗体。

4. 步骤5:青蛙抗体群的促进与抑制。当记忆青蛙群体N1中抗体浓度的最大值cmax低于抗体浓度阈值th时, 记忆青蛙群体中的抗体处于多样化;否则抗体趣于一致化, 随机产生的新个体代替被淘汰的浓度大的个体。用检测记忆青蛙群体N2去检测N中是否含有已搜索过的抗体 (即N2中记录的抗体) , 如果有就用随机青蛙抗体取代它。

5. 步骤6:将促进记忆青蛙群体N1与检测后的青蛙抗体群N相结合生成新的青蛙抗体种群, 将F只青蛙按适应值降序排列分为m子群体, 对每一个子群体中的青蛙个体找出其最优个体和最差个体, 在指定迭代次数内提高差个体的适应值, 针对各个子群体, 按适应值降序排列体, 进行重新分配和混合蛙跳运算;

6. 步骤7:终止条件是否满足?如果满足, 结束迭代, 否则转向Step3。

2 基于ISFLA优化的WNN预测模型
2.1 WNN模型的原理与结构
小波神经网络是一种结合小波分析和神经网络而提出的一种前馈神经网络。一般的WNN模型用小波函数代替Sigmoid函数作为隐含层的激活函数, 既具有神经网络的学习能力、泛化能力及非线性映射能力, 又具有小波变换的多尺度时频分析手段和良好的逼近特性。本文采用只含有一个隐含层的3层网络。网络的隐层神经元采用小波函数做激励函数, 输出层神经元采用Sigmoid函数做激励函数。

设输入的样本的个数为m, 输入层节点的个数为p, 隐含层节点的个数为n, 输出层节点的个数为q;wij为连接输出层节点与隐含层节点的连接权值, wjk为连接隐含层节点与输入层节点的连接权值, θj为隐含层节点的阈值, θi为输出层节点的阈值, aj和bj分别为第j个隐含层节点的伸缩系数和平移系数;则上述WNN模型可表示为:

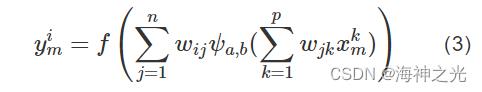
式中:f (x) 为Sigmoid函数, 即f (x) =1/[1+exp (-x) ]。

由于Morlet小波基对干扰的鲁棒性好、误差小、计算稳定等特点[10], ψ (x) 采用较多使用的Morlet母小波

ψ (x) cos (1.75x) exp (-x2/2) (4)

单结点输出时, 网络输出的均方误差 (mean square error, MSE) 为

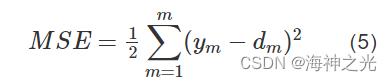
WNN模型采用梯度下降法训练网络, 利用前馈网络反向传播误差, 不断地调整、优化、确定网络的权值和尺度因子、平移因子, 节点之间的权重值与阈值, 使网络计算输出与期望输出拟合最优, 即MSE最小。

2.2 ISFLA-WNN模型的实现
2.2.1 确定算法的参数
根据WNN模型的输入输出样本集确定网络的拓扑结构并作规范化处理, 对优化的网络参数进行编码, 将神经网络的各连接权值、各阈值、伸缩平移系数作为青蛙个体。

2.2.2 初次优化网络参数
利用免疫蛙跳算法对WNN模型参数 (权值、阈值、伸缩平移系数) 进行初次优化, 代替了神经网络参数初始的随机赋值, 克服了仅凭借误差的传播作为修正法则的弊端。

2.2.3 适应值评价
根据ISFLA算法, 以WNN模型的均方差MSE作为青蛙种群搜索性能的评价指标, 适应度越高, 网络实际输出和期望输出的误差越小, 记录最佳个体适应度值, 及其对应的青蛙个体, 该青蛙个体就是下次迭代中WNN模型的最优网络参数。

2.2.4 判断中止条件
判断适应度值是否达到最大误差设定值以及迭代次数是否达到最大迭代步数, 若不满足条件, 按免疫蛙跳算法进行更新, 并生成新一代种群, 返回 (2) ;如果满足条件, 将全局最优青蛙个体映射为WNN网络的权值、域值、伸缩平移系数, 得到一个建立好参数的WNN网络。

2.2.5 进行WNN模型操作, 生成最优解
将上述方法得到的最优解作为WNN网络的初始权值、域值、伸缩平移系数, 对这些参数用WNN模型的梯度下降法进行二次优化训练直到网络达到性能指标, 经过以上训练, 改进的免疫蛙跳算法优化的小波神经网络达到最佳状态, 将该状态下的最终网络参数用于水稻的需水量预测, 输出预期结果。

⛄二、部分源代码

clear;
data=JustLoad();
warning(‘off’);
% Inputs (Train and Test)
inputs=rescale(data.TrainInputs)‘;
TstInputs=rescale(data.TestInputs)’;

% Targets (Train and Test)
targets=rescale(data.TrainTargets)‘;
TstTargets=rescale(data.TestTargets)’;

sizenn=size(inputs);sizenn=sizenn(1,1);

% Number of neurons----------------------
n = 12;
%----------------------------------------

% ‘trainlm’ Levenberg-Marquardt
% ‘trainbr’ Bayesian Regularization (good)
% ‘trainbfg’ BFGS Quasi-Newton
% ‘trainrp’ Resilient Backpropagation
% ‘trainscg’ Scaled Conjugate Gradient
% ‘traincgb’ Conjugate Gradient with Powell/Beale Restarts
% ‘traincgf’ Fletcher-Powell Conjugate Gradient
% ‘traincgp’ Polak-Ribiére Conjugate Gradient
% ‘trainoss’ One Step Secant (good)
% ‘traingdx’ Variable Learning Rate Gradient Descent
% ‘traingdm’ Gradient Descent with Momentum
% ‘traingd’ Gradient Descent
% Creating the NN ----------------------------
net = feedforwardnet(n,‘traingdx’);
%---------------------------------------------

% configure the neural network
[net tr]= train(net,inputs, targets);
perf = perform(net,inputs, targets);%mse

% Current NN Weights and Bias
% Create Handle for Error
h = @(x) NMSE(x, net, inputs, targets);

%% SFLA NN
[x, err_ga] = sfla(h, sizenn*n+n+n+1);
%-----------------------------------------

net = setwb(net, x’);
% Optimized NN Weights and Bias
getwb(net);
% Error for Optimized NN
Error = targets - net(inputs);
calc = mean(Error.^2)/mean(var(targets’,1));

%-----------------------------------------
Outputs=net(inputs);
TestOutputs=net(TstInputs);

% Train
TrMSE=mse(targets,Outputs);
TrRMSE=sqrt(TrMSE);
TrMAE=mae(targets,Outputs);
TrCC= corrcoef(targets,Outputs);
TrR_Squared=TrCC*TrCC;

%Test
TsMSE=mse(TstTargets,TestOutputs);
TsRMSE=sqrt(TsMSE);
TsMAE=mae(TstTargets,TestOutputs);
TsCC = corrcoef(TstTargets,TestOutputs);
TsR_Squared=TsCC*TsCC;

% Statistics
% Train
fprintf(‘Training “MSE” Is = %0.4f.\\n’,TrMSE)
fprintf(‘Training “RMSE” Is = %0.4f.\\n’,TrRMSE)
fprintf(‘Training “MAE” Is = %0.4f.\\n’,TrMAE)
fprintf(‘Training “Correlation Coefficient” Is = %0.4f.\\n’,TrCC(1,2))
fprintf(‘Training “R_Squared” Is = %0.4f.\\n’,TrR_Squared(1,2))
% Test
fprintf(‘Testing “MSE” Is = %0.4f.\\n’,TsMSE)
fprintf(‘Testing “RMSE” Is = %0.4f.\\n’,TsRMSE)
fprintf(‘Testing “MAE” Is = %0.4f.\\n’,TsMAE)
fprintf(‘Testing “Correlation Coefficient” Is = %0.4f.\\n’,TsCC(1,2))
fprintf(‘Testing “R_Squared” Is = %0.4f.\\n’,TsR_Squared(1,2))
view(net);

⛄三、运行结果

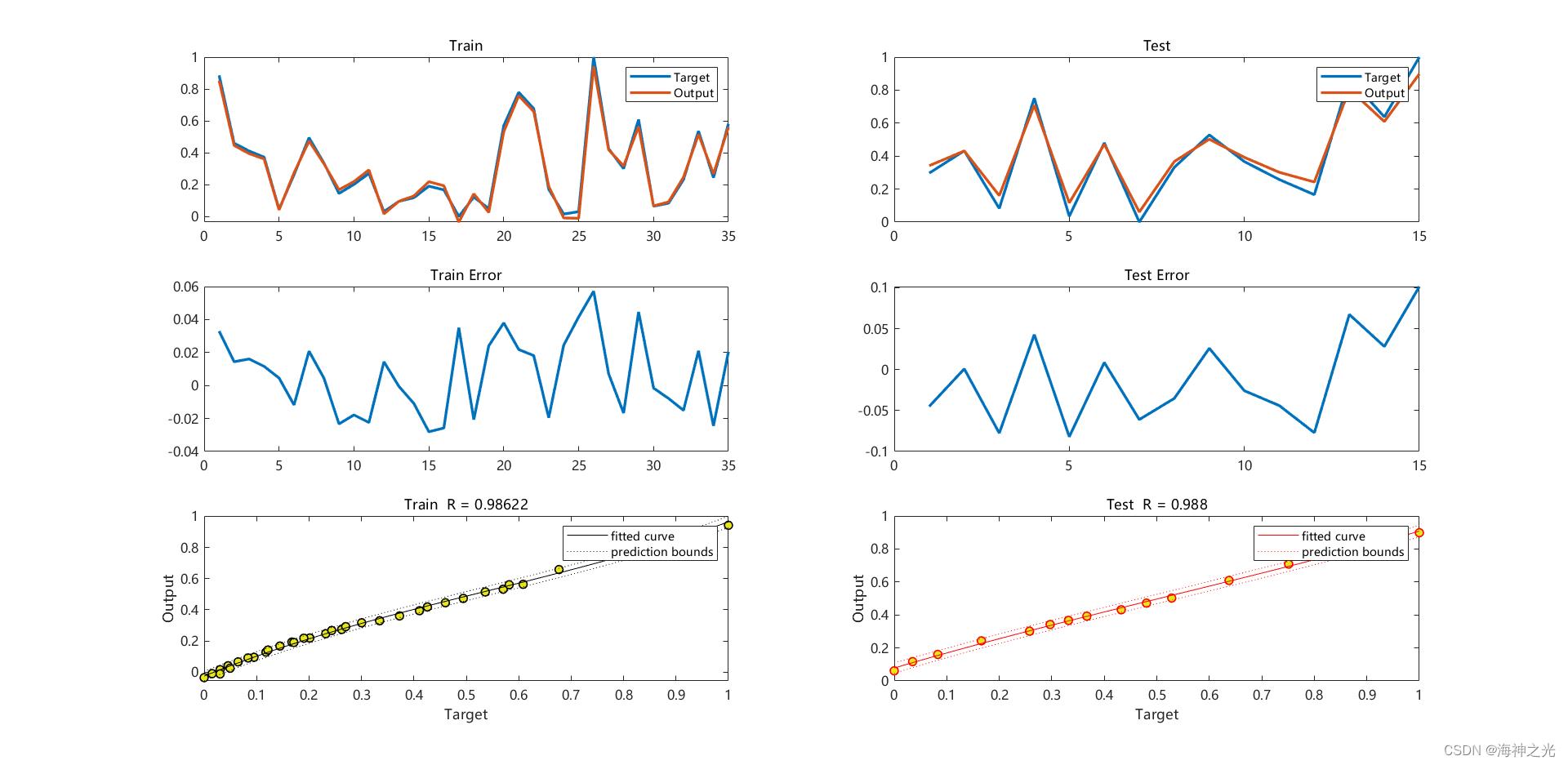
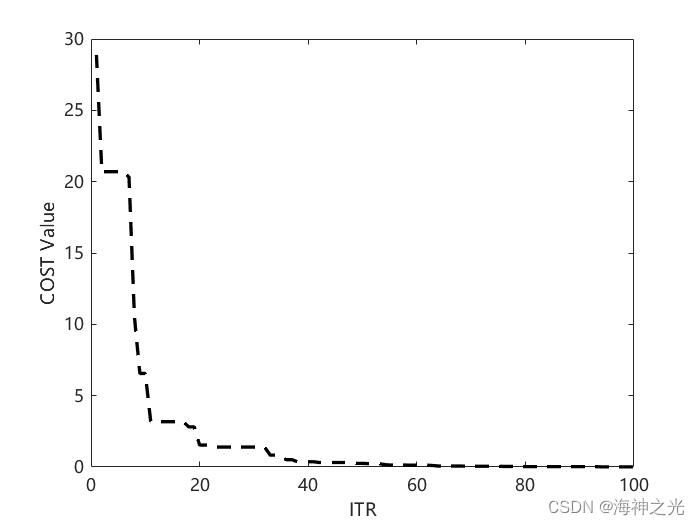
⛄四、matlab版本及参考文献

1 matlab版本
2014a

2 参考文献
[1]李琳,隋树涛.基于免疫蛙跳算法的小波神经网络的水稻需水量预测[J].黑龙江水利科技. 2012,40(03)

3 备注
简介此部分摘自互联网，仅供参考，若侵权，联系删除