青蛙跳台阶问题

Posted 2023-02-27 fy_闷油瓶

C语言中青蛙跳台阶问题

问题描述

有一只青蛙，一次可以跳一层台阶也可以跳两层台阶，问n层台阶共有多少种跳法？

解决方法

首先假设当有n层时，有f（n）种跳法

一、n<=2时
n=1，只有一种跳法，即跳一层
f(1)=1;
当n=2时，有两种跳法：

1. 直接跳2层
2. 跳2次，每次跳1层，1+1=2

f(2)=2;

二、n>2时
n=3，第一跳有两种跳法:

1. 跳1层，剩下2层
   剩下的两层又回到了n=2时的情况（可以理解为，青蛙现在处在第一层台阶上，还剩下两层，有几种跳法）,因此又有两种跳法
2. 跳2层，剩下1层

因此n=3时有3种跳法:
1+1+1
1+2
2+1
f(3)=f(2)+f(1)=3;

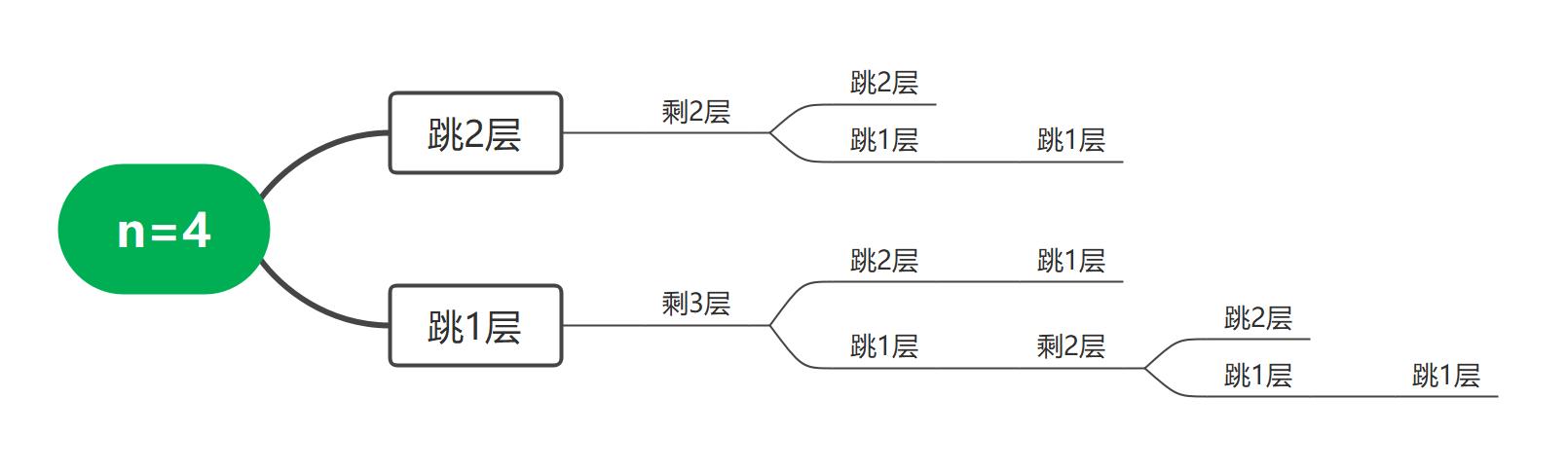
n=4，第一跳还是有两种跳法:

1. 跳1层，剩下3层
   剩下的两层回到了n=3时的情况(可以看做青蛙处在第一层，还需要跳3层，这3层有多少种跳法)，n=3时有3种跳法
2. 跳2层，剩下2层
   剩下的2层回到了n=2的情况，n=2时有2种跳法

因此n=4时有3+2+5种跳法（其中3是跳3层的跳法，2是跳2层的跳法）
f(4)=f(3)+f(2)=5

n=5时，第一跳也是有两种跳法，跳1层和跳2层：
跳1层，则剩4层，4层的跳法有5种；
跳2层，则剩3层，3层的跳法有3种；
所以n=5时共有5+3=8种跳法
f(5)=f(4)+f(3)=8
…
…
…
当n=k时，第一跳还是有两种，跳1层和跳2层：
跳1层，剩k-1层；
跳2层，剩k-2层；
所以n=k时
f(k)=f(k-1)+f(k-2);
这样就构造出了迭代关系式

代码

一、函数递归

#include<stdio.h>


int jump(int n)   //跳n个台阶有多少方法

	int cnt = 0;   //计数器
	if (n == 1)  //当只有一个台阶时，只有一种跳法
		cnt = 1;
	else if (n == 2)  //当有两个台阶时，有两种跳法
		cnt = 2;
	else
		//当n>2时，第一跳有两种跳法，即1个台阶或者两个台阶，分别剩下(n-1)和(n-2)个台阶
		cnt = jump(n - 1) + jump(n - 2);
	return cnt;  


int main()


	int count,n=0;   //n阶台阶
	scanf("%d", &n);
	count=jump(n);
	printf("%d\\n", count);
	return 0;

当台阶数较多时（在我的电脑上，当n>30）时能明显感觉到计算速度很慢。在函数递归的时候，重复计算的次数会很多，例如当n=30时，需要计算f(29)和f(28)，而计算f(29)时又要重新继续算f(28)，f(28)就被重复计算了1次，而f(3)被重复计算的次数更多，因此程序会很慢。
二、循环

#include<stdio.h>


int jump(int n)   //跳n个台阶有多少方法

	int n1 = 2, n2 = 1;   //n1,n2分别表示上一次和上上次的值
	int cnt = 0;        //计数器
	if (n <= 2)         //当n=1时，有1种方法；n=2时有2种方法
		cnt = n;
	for (; n > 2; n--)  
	
		cnt = n1 + n2;  //n>2时，本次的值为上一次和上上次值的和            
		n2 = n1;       //将n1的值变成下一次的上上次
		n1 = cnt;     //将cnt的值变成下一次的上一次
	
	return cnt;


int main()


	int count,n=0;   //n阶台阶
	scanf("%d", &n);
	count=jump(n);
	printf("%d\\n", count);
	return 0;