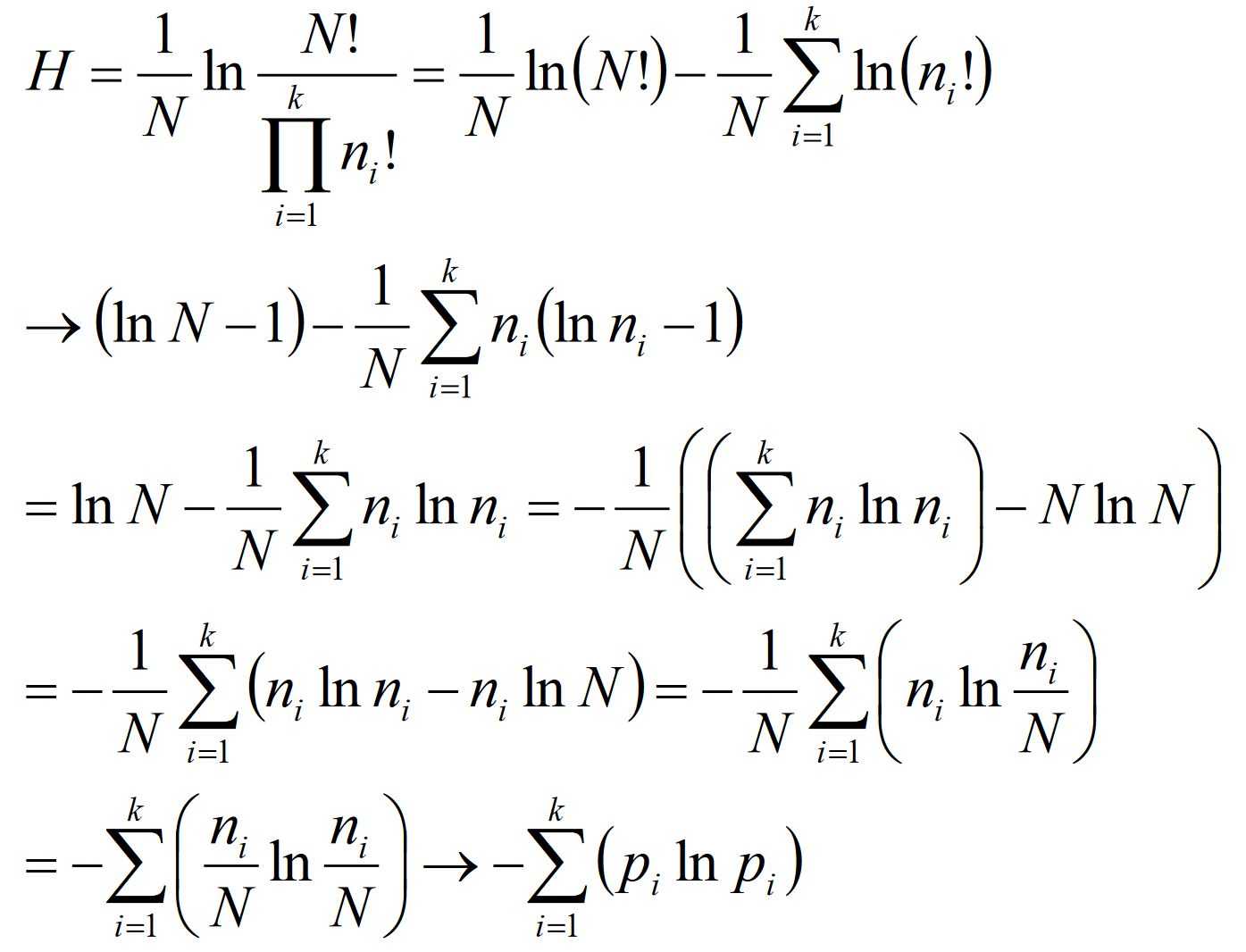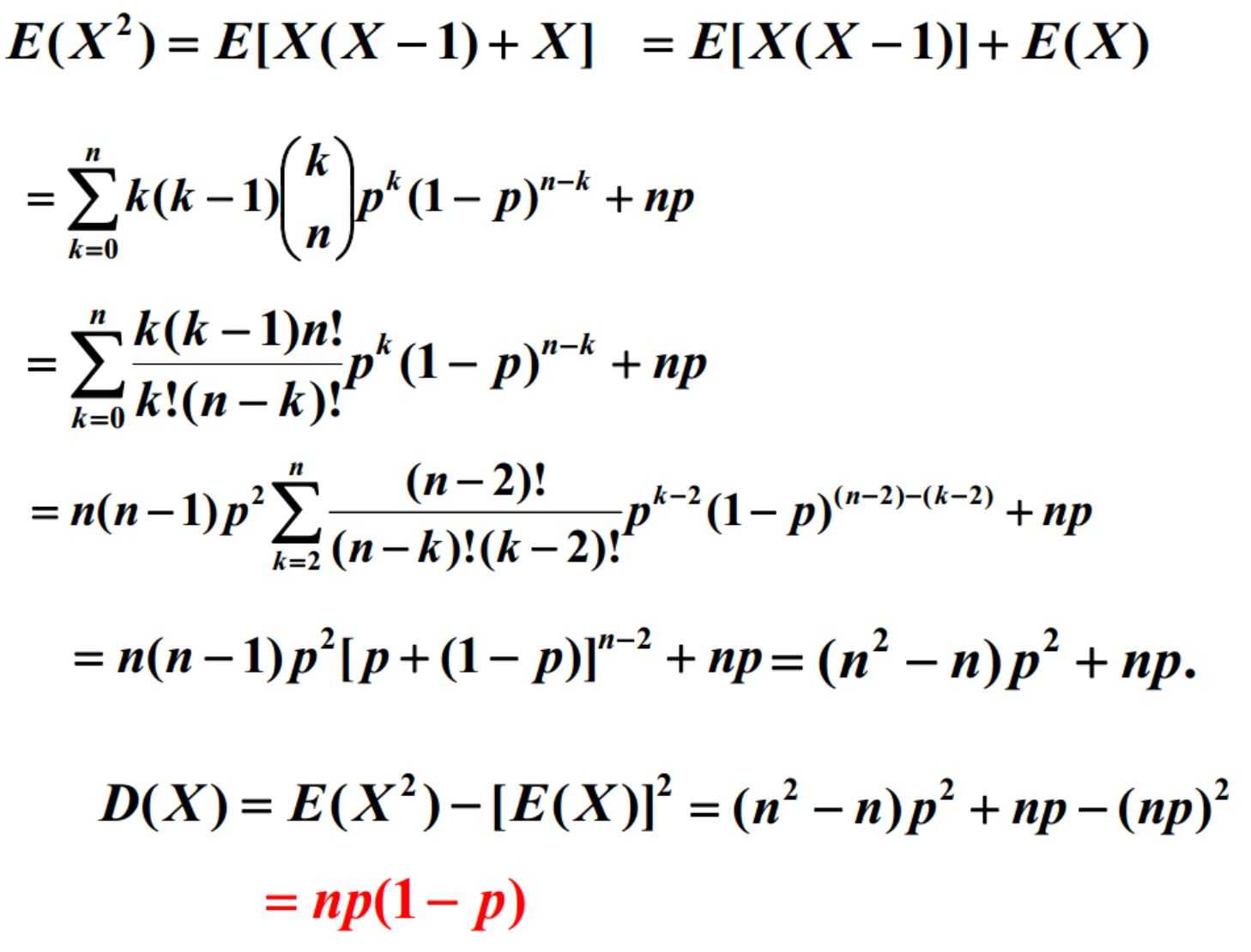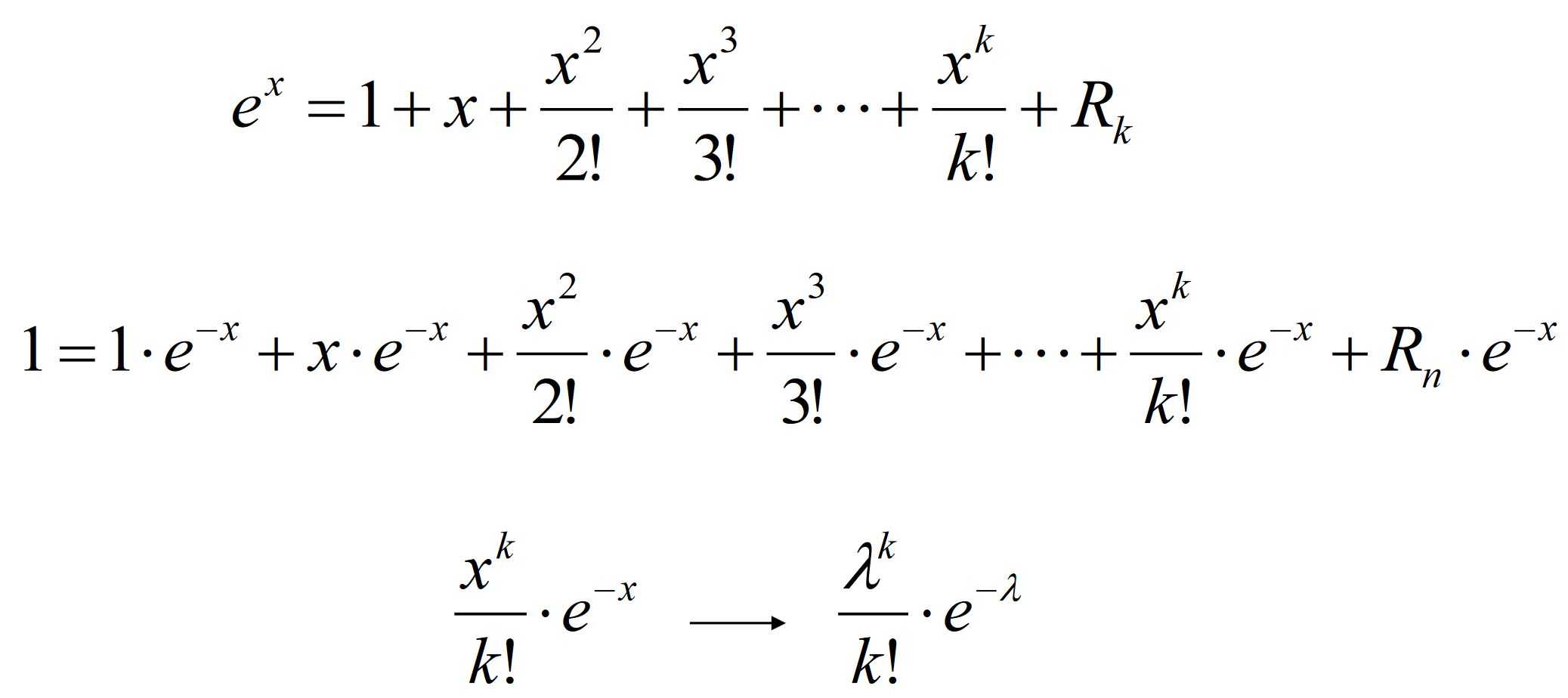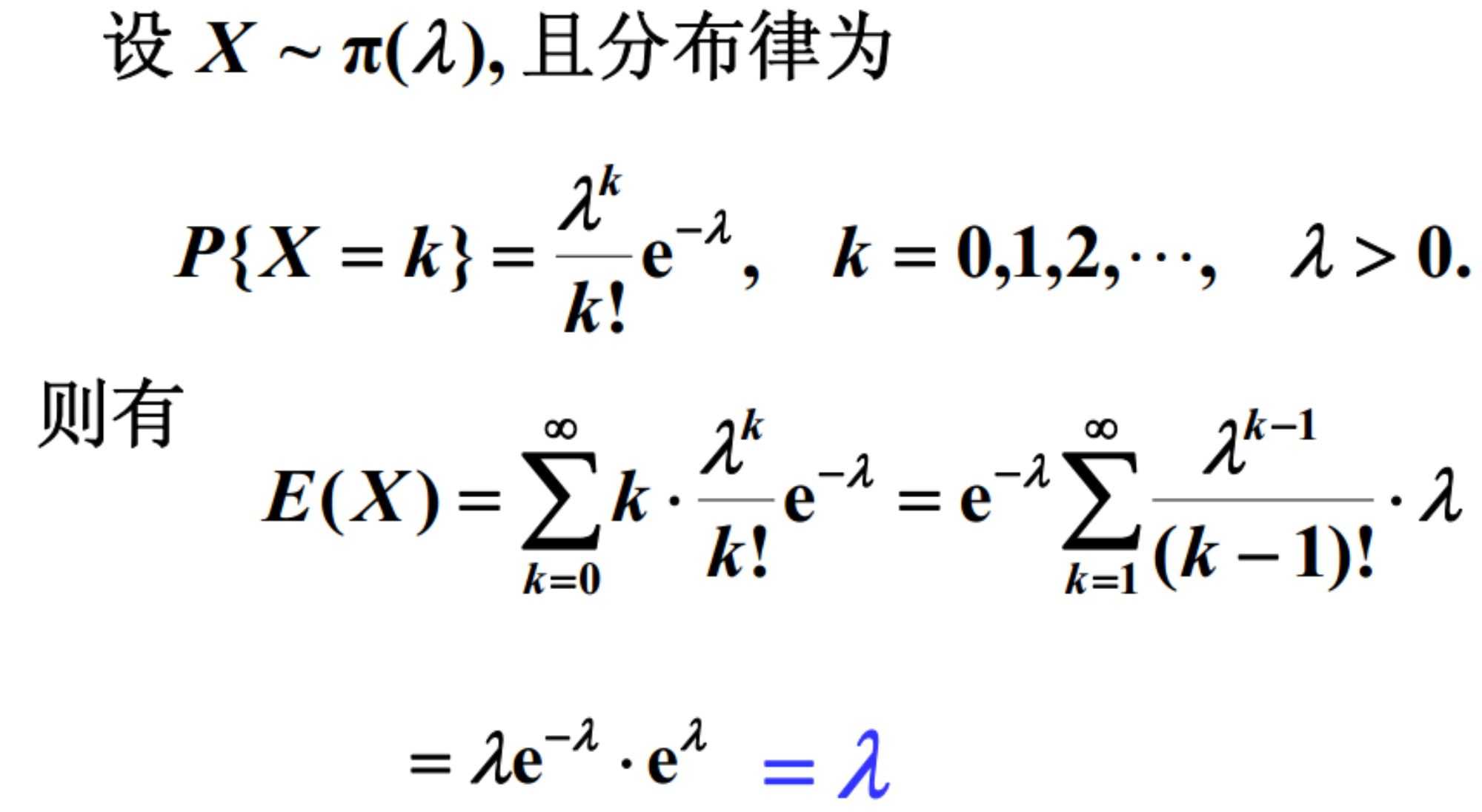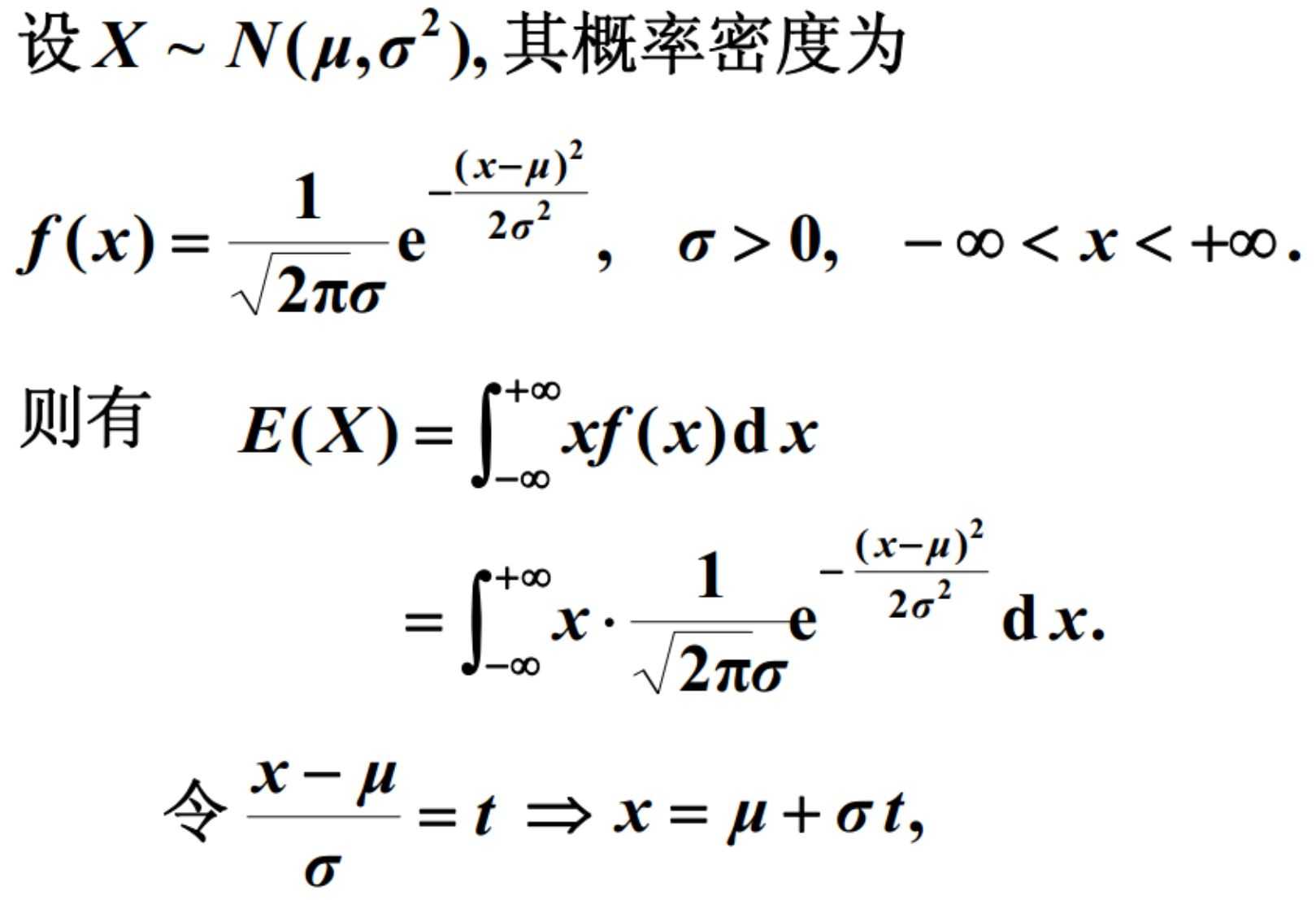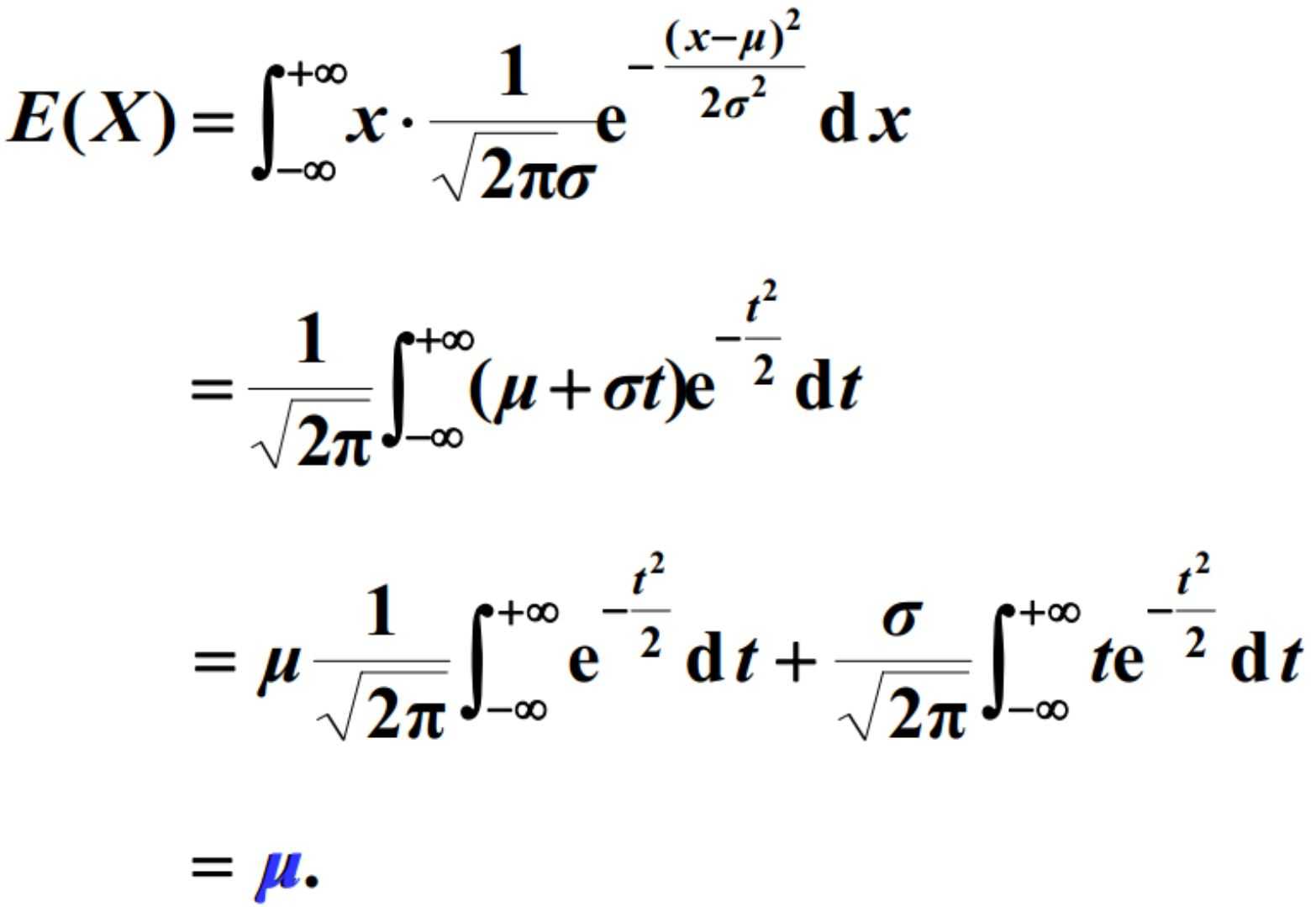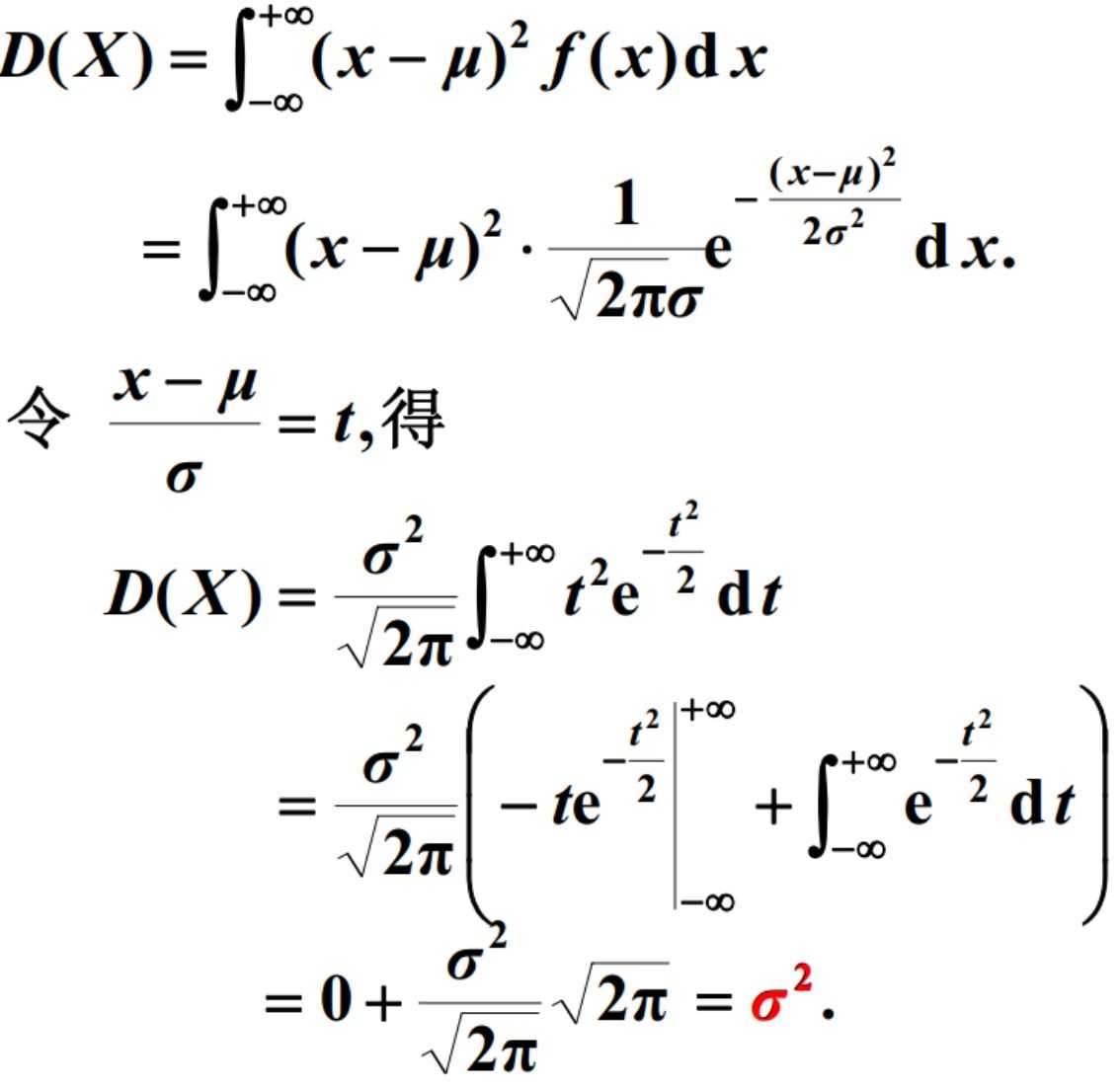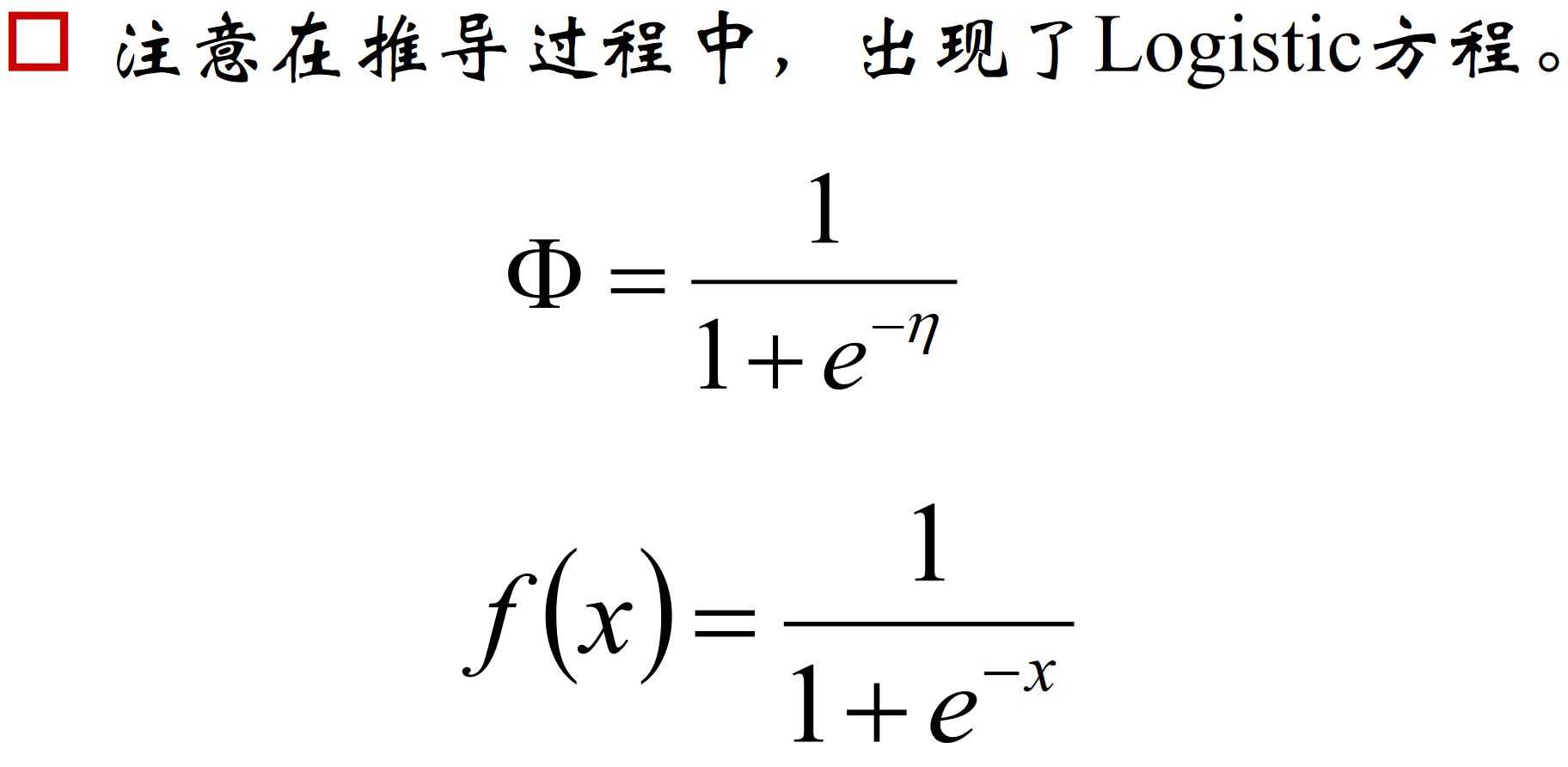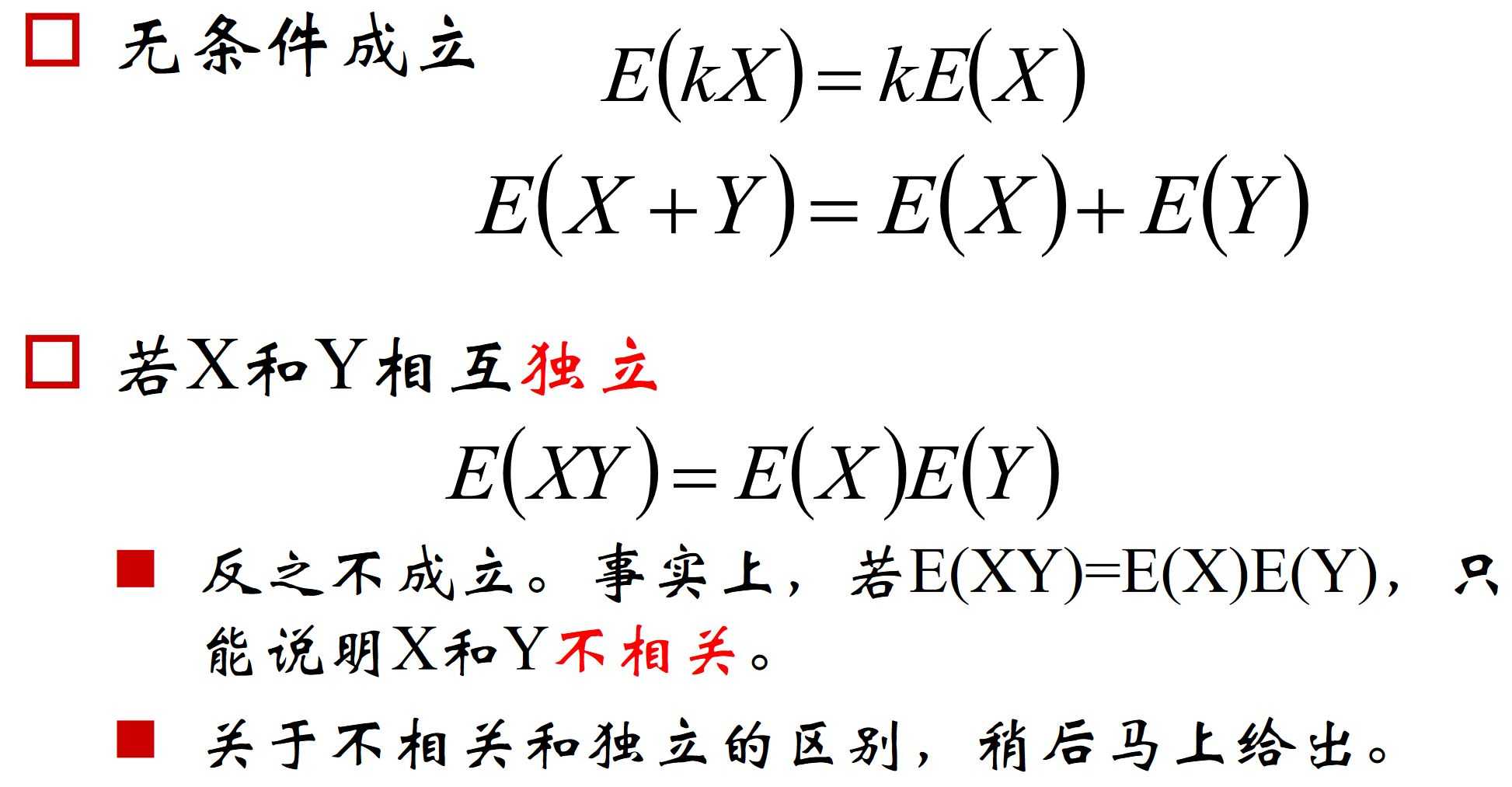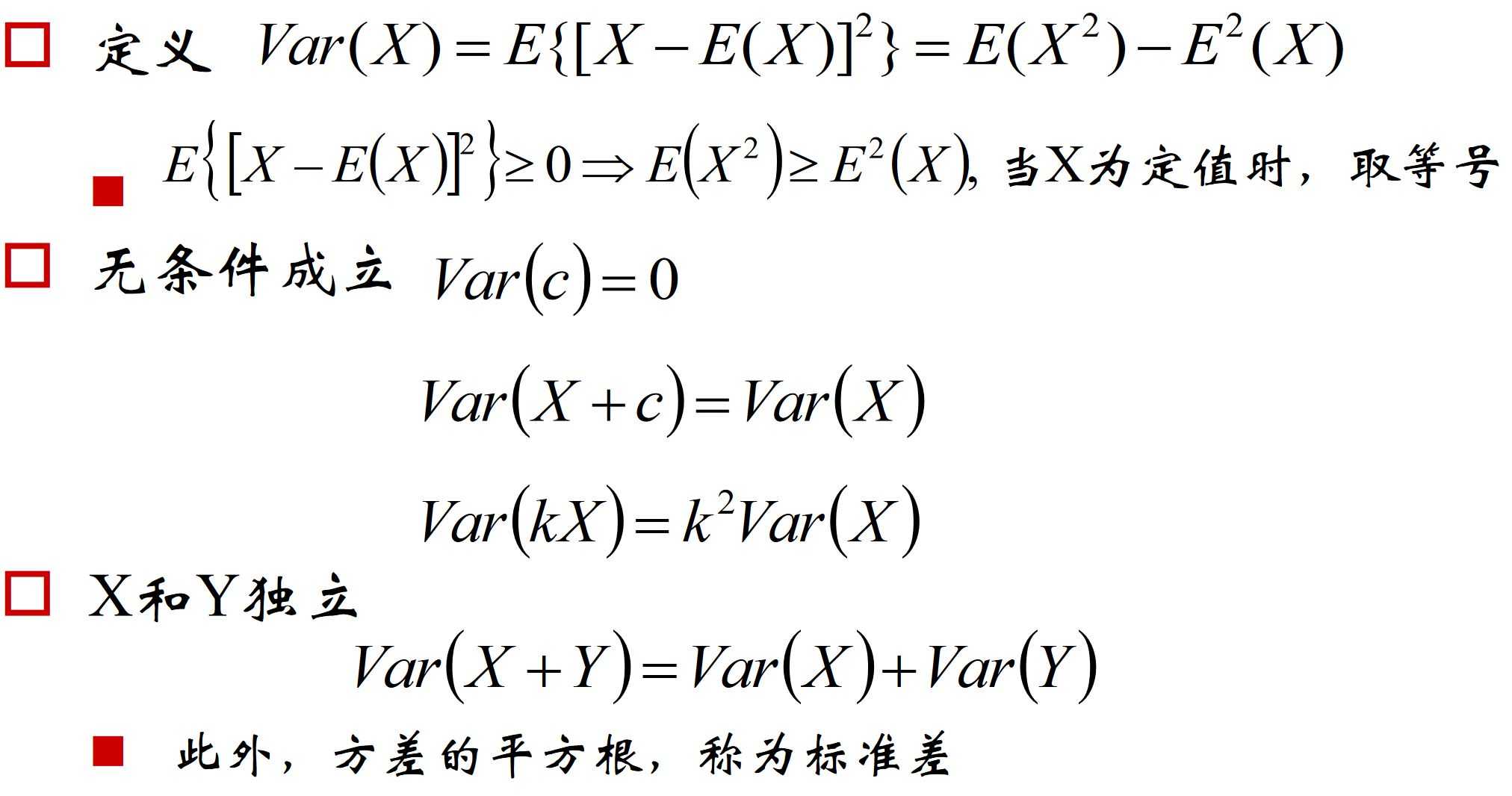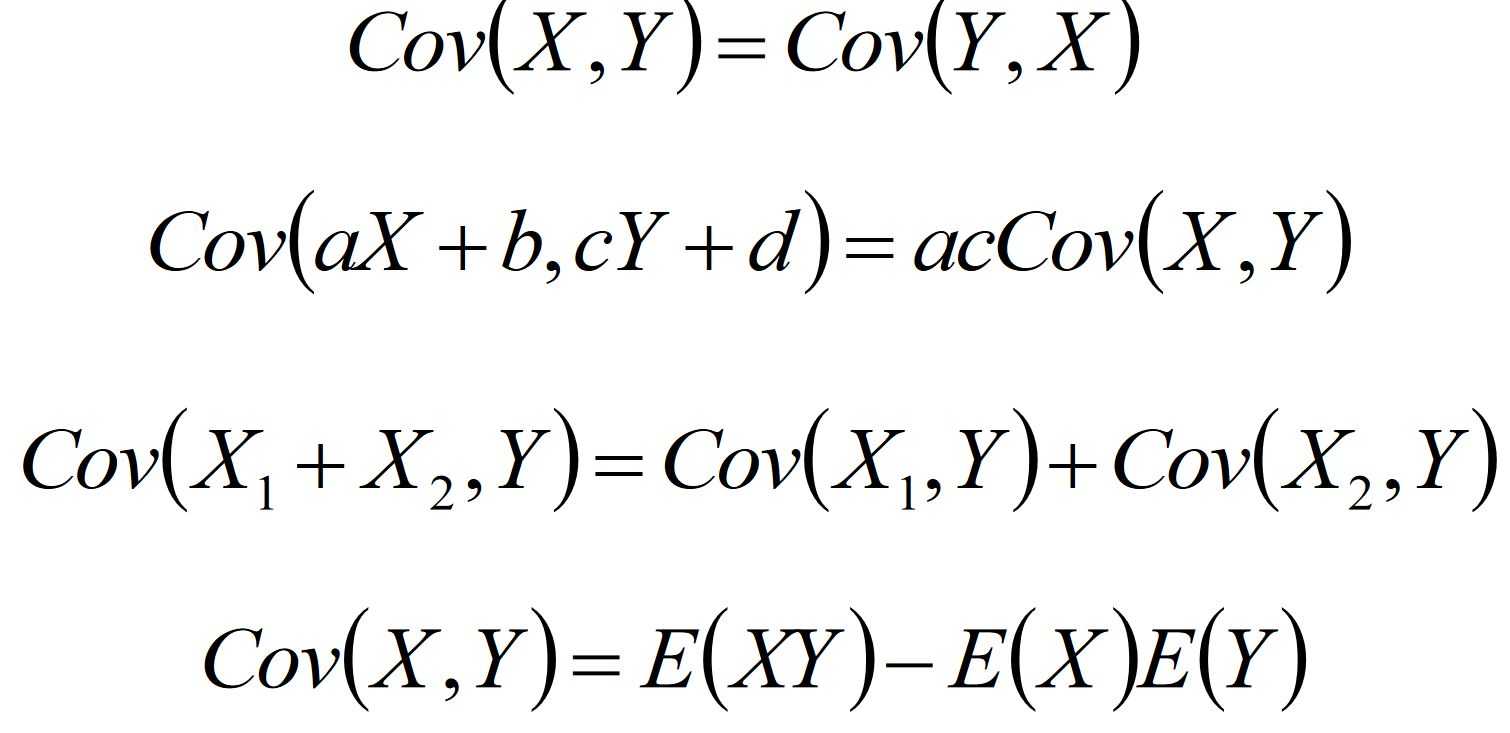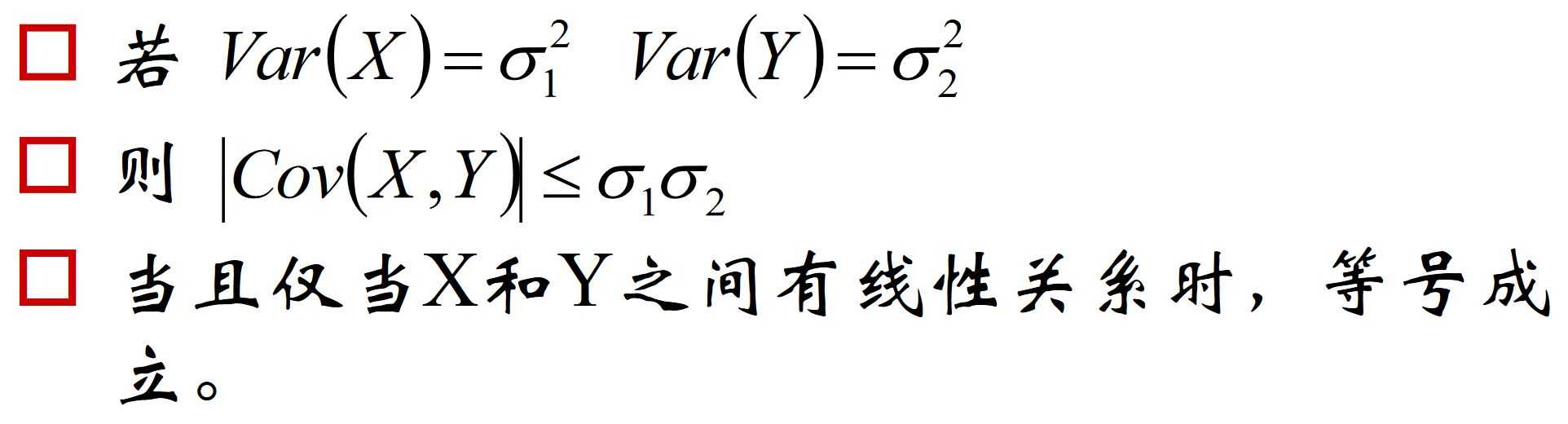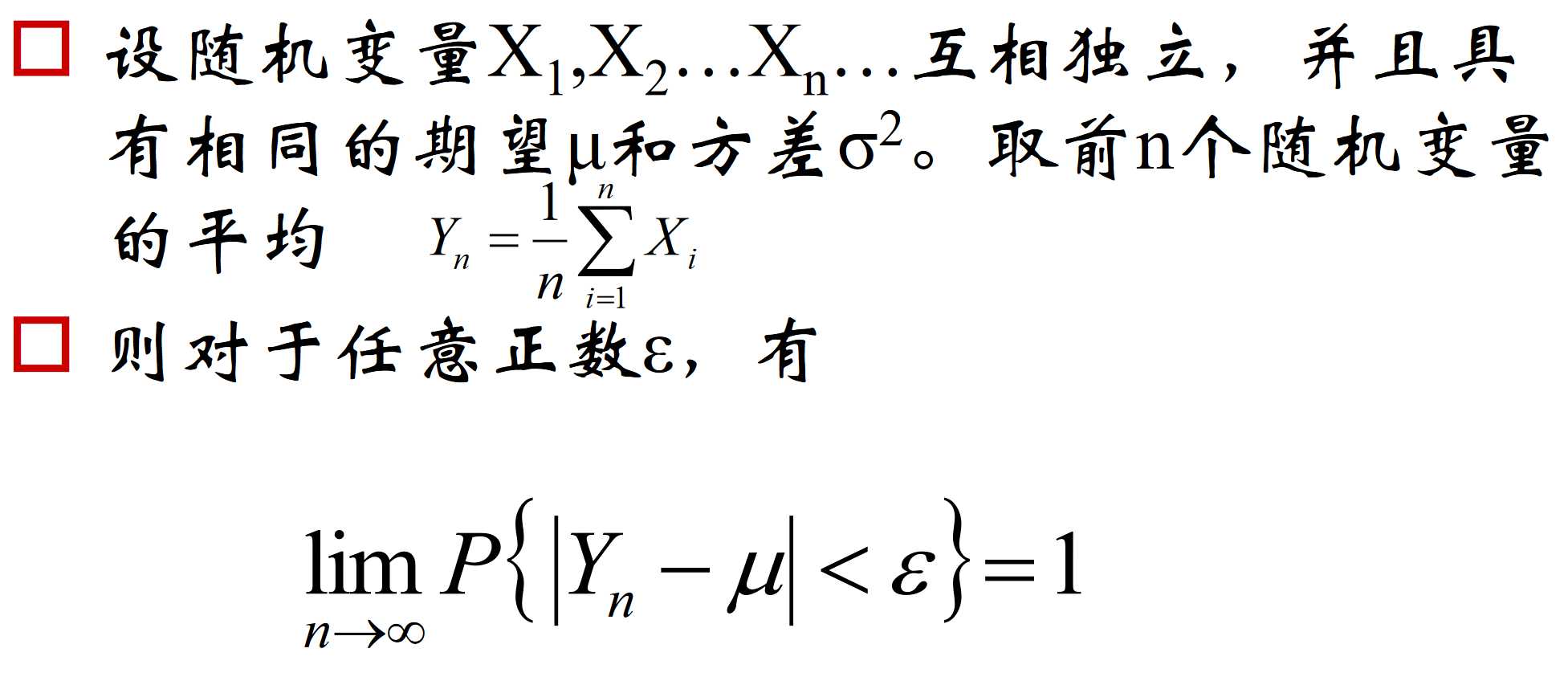机器学习升级版（VII）——第2课 概率论与贝叶斯先验

Posted 2020-11-17 lxr1995

摘录自：邹博《机器学习升级版》课件

1. 概率论基础

• 1.初步认识

  • 

• 2.古典概型

  • 
  • 

• 3.生日悖论

  • 生日悖论（Birthday paradox）是指，如果一个房间里有23个或23个以上的人，那么至少有两个人的生日相同的概率要大于50%。这就意味着在一个典型的标准小学班级(30人)中，存在两人生日相同的可能性更高。对于60或者更多的人，这种概率要大于99%。从引起逻辑矛盾的角度来说生日悖论并不是一种悖论，从这个数学事实与一般直觉相抵触的意义上，它才称得上是一个悖论。大多数人会认为，23人中有2人生日相同的概率应该远远小于50%。

• 4.装箱问题

  • 
  • 

• 5.与组合数的关系

  • 

• 6.组合数背后的密码  

  • 

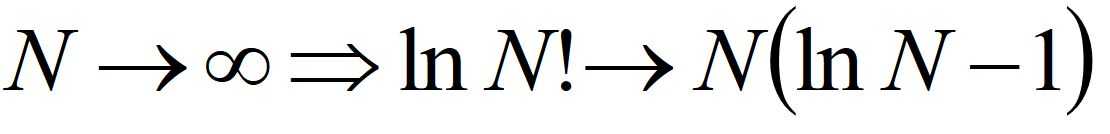
• 7.统计数值的概率

  • 

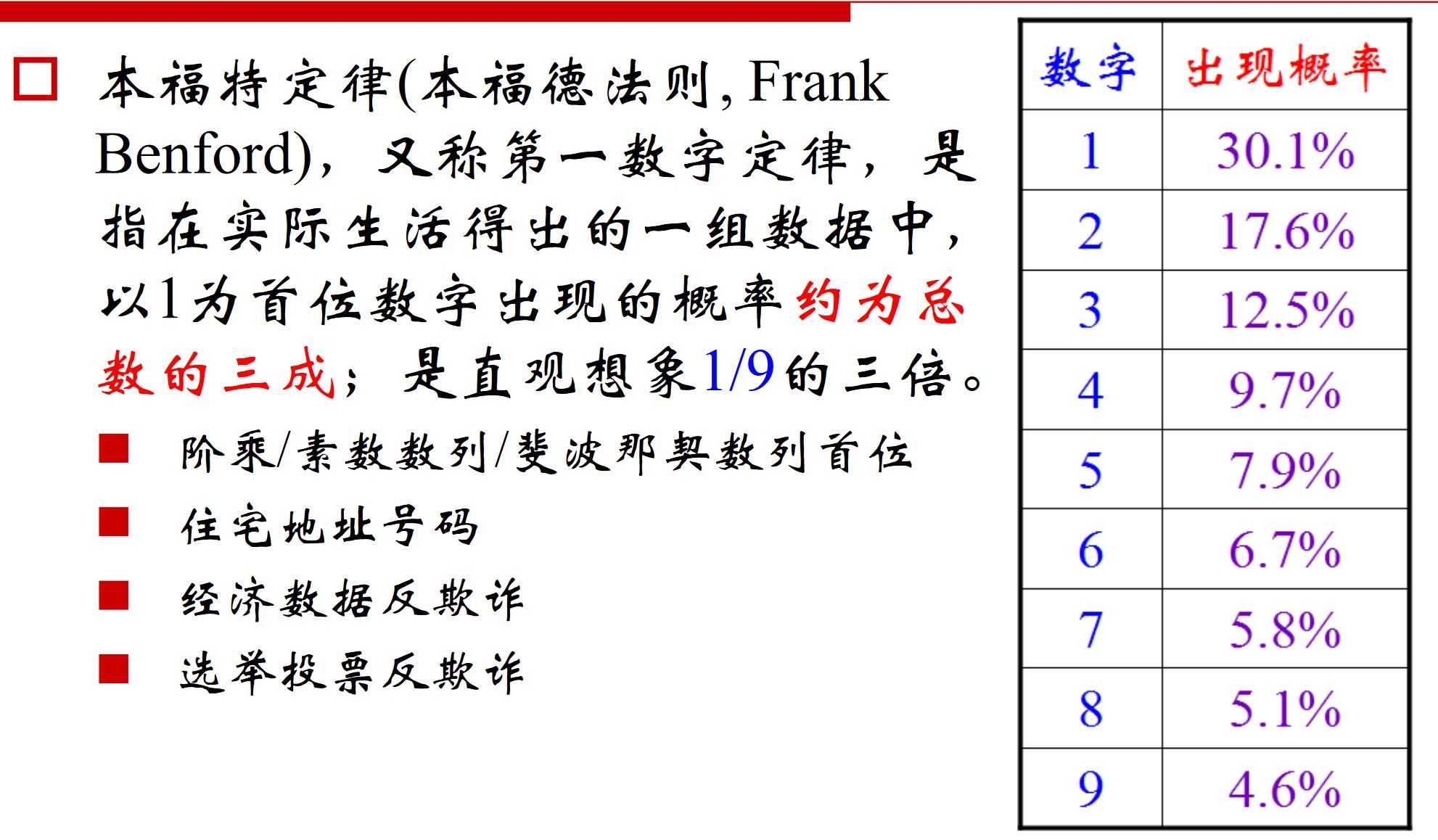
• 8.本福特定律

  • 

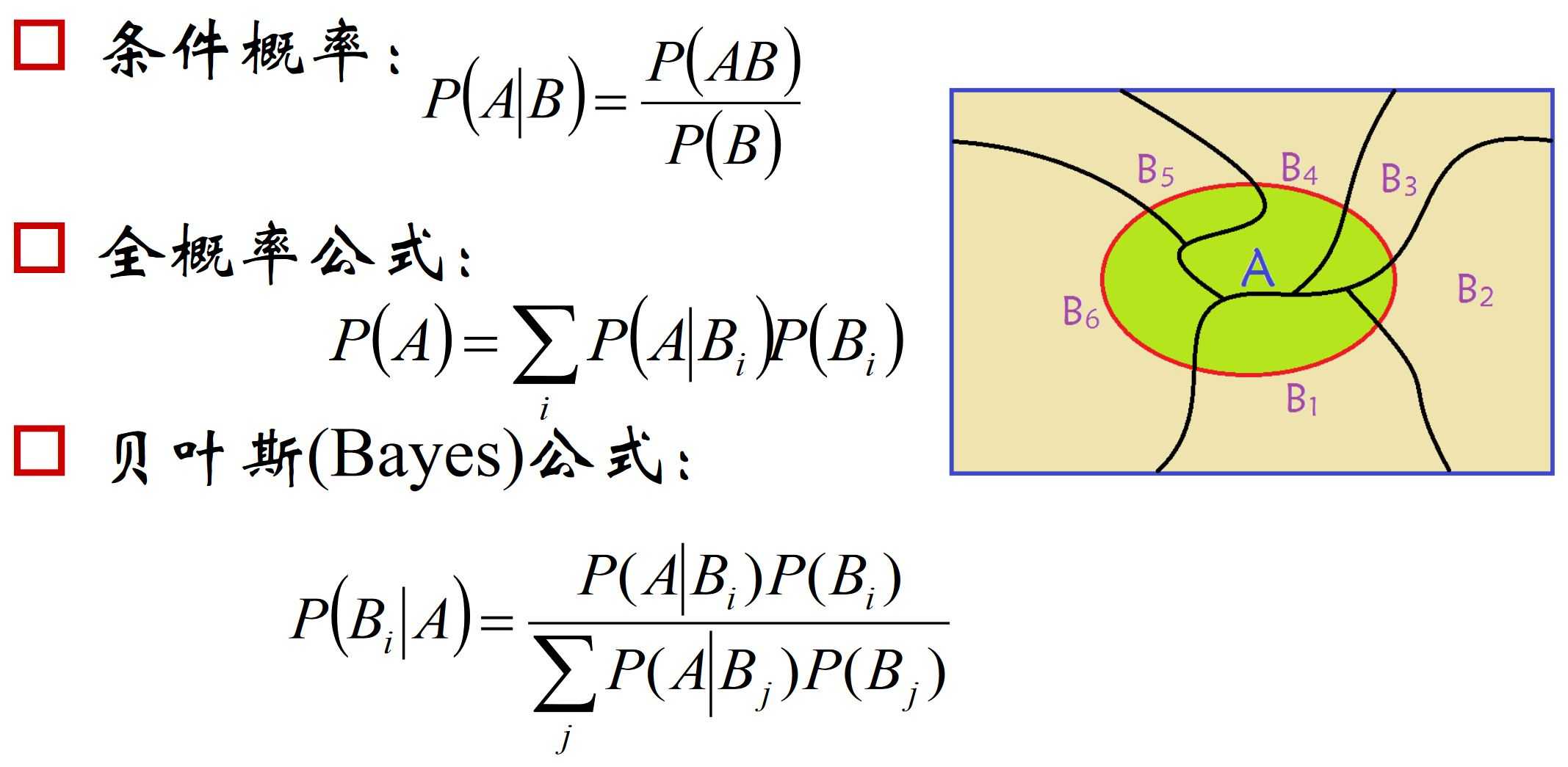
• 9.概率公式

  • 

• 10.贝叶斯公式  

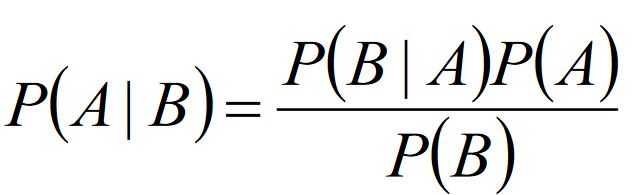
  • 定义：
    
    • 
  • 应用：
    
    • 

• 11.分布

  • 常见分布是可以完美统一为一类分布

  • 1.两点分布 Bernoulli distribution

    • 

  • 2.二项分布  Binomial Distribution

    
    
    • 
    • 
    • 

  • 3.负二项分布

    • 

  • 考察Taylor展式

    • 

  • 4.泊松分布 Poisson distribution

    • 
    • 
    • 

  • 5.均匀分布 Uniform Distribution

    • 

  • 6.指数分布 Exponential Distribution

    • 
    • 
    • 

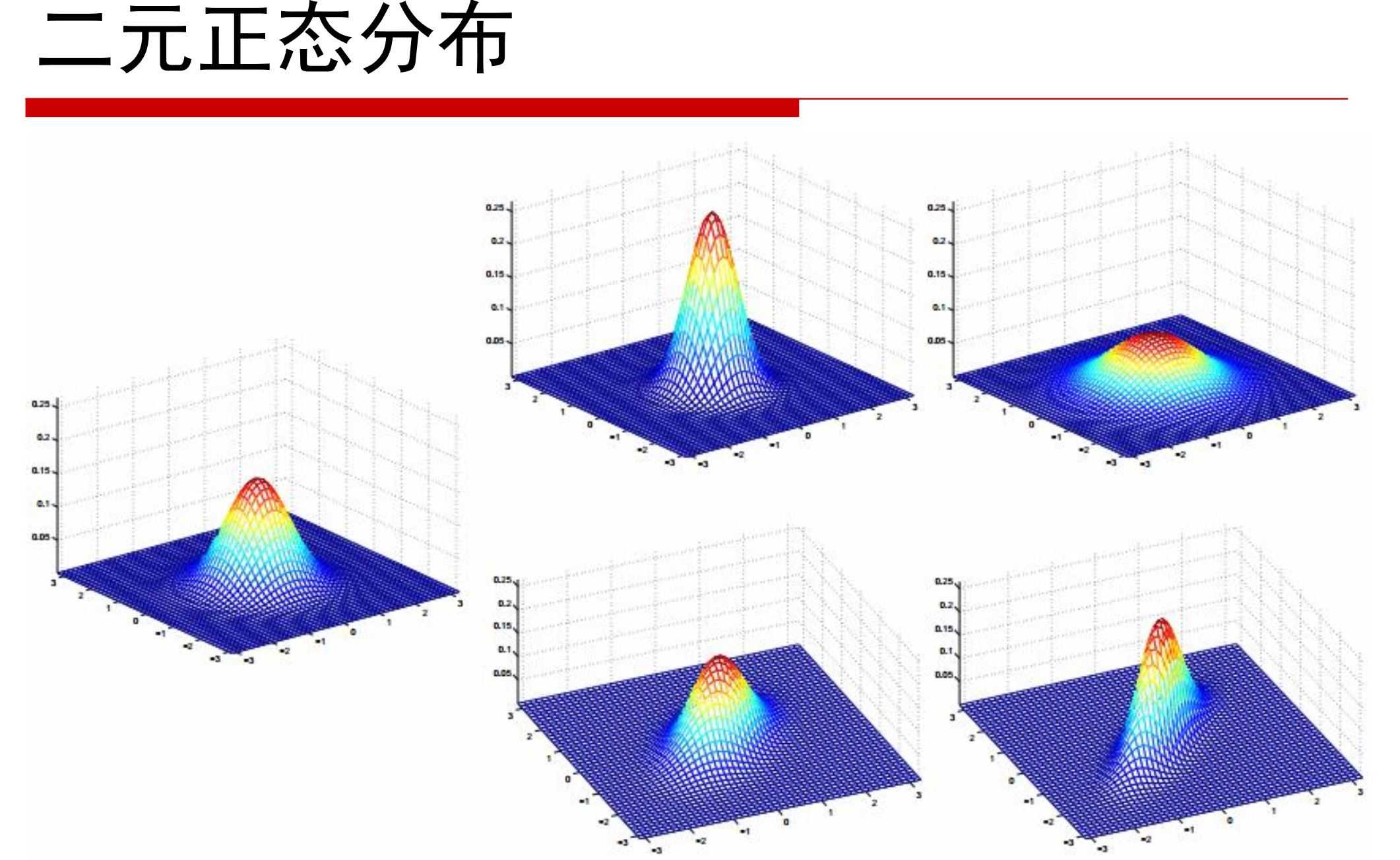
  • 7.正态分布Normal/高斯分布Gaussian distribution

    • 
    • 
    • 
    • 

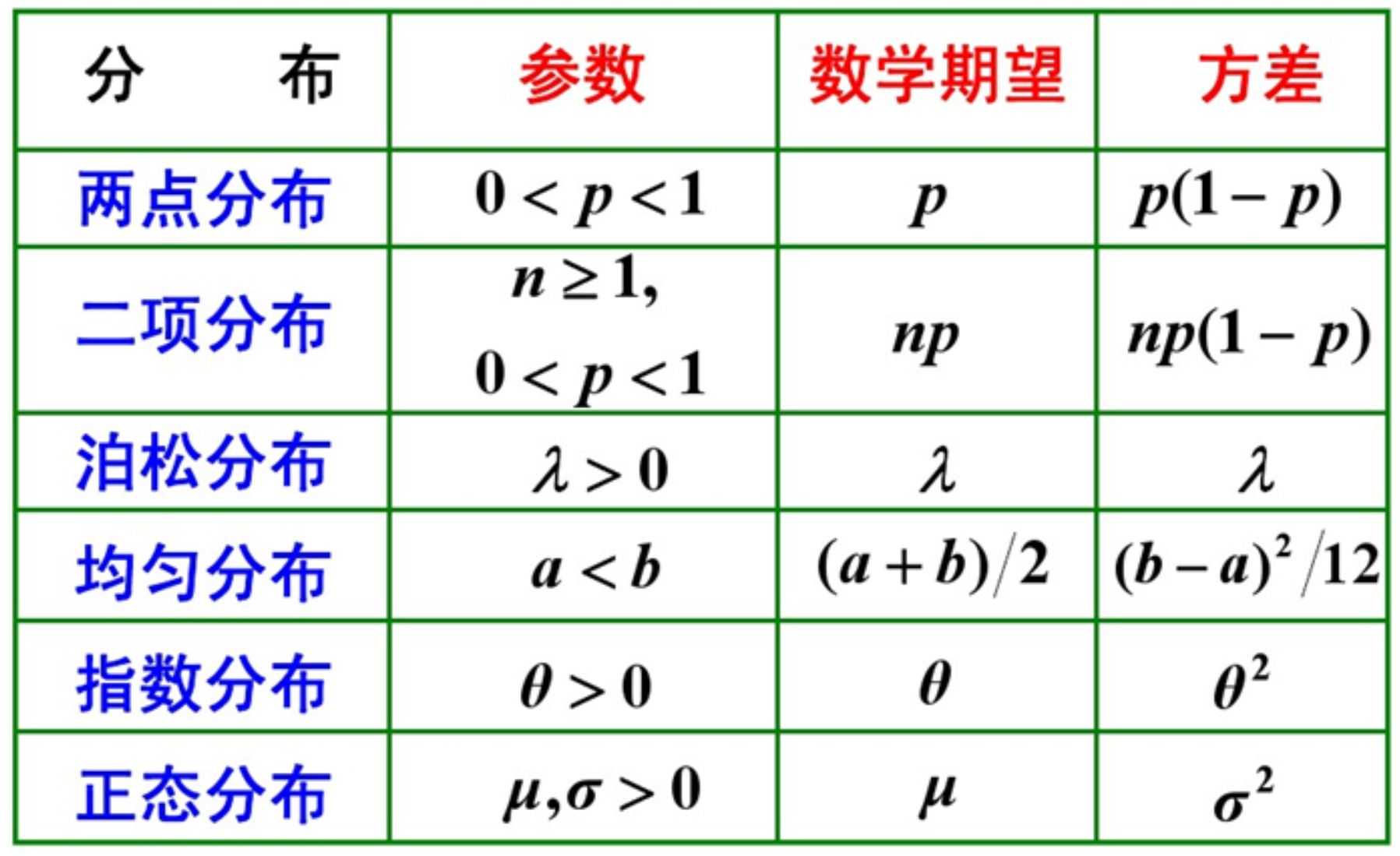
  • 上述分布总结

    • 

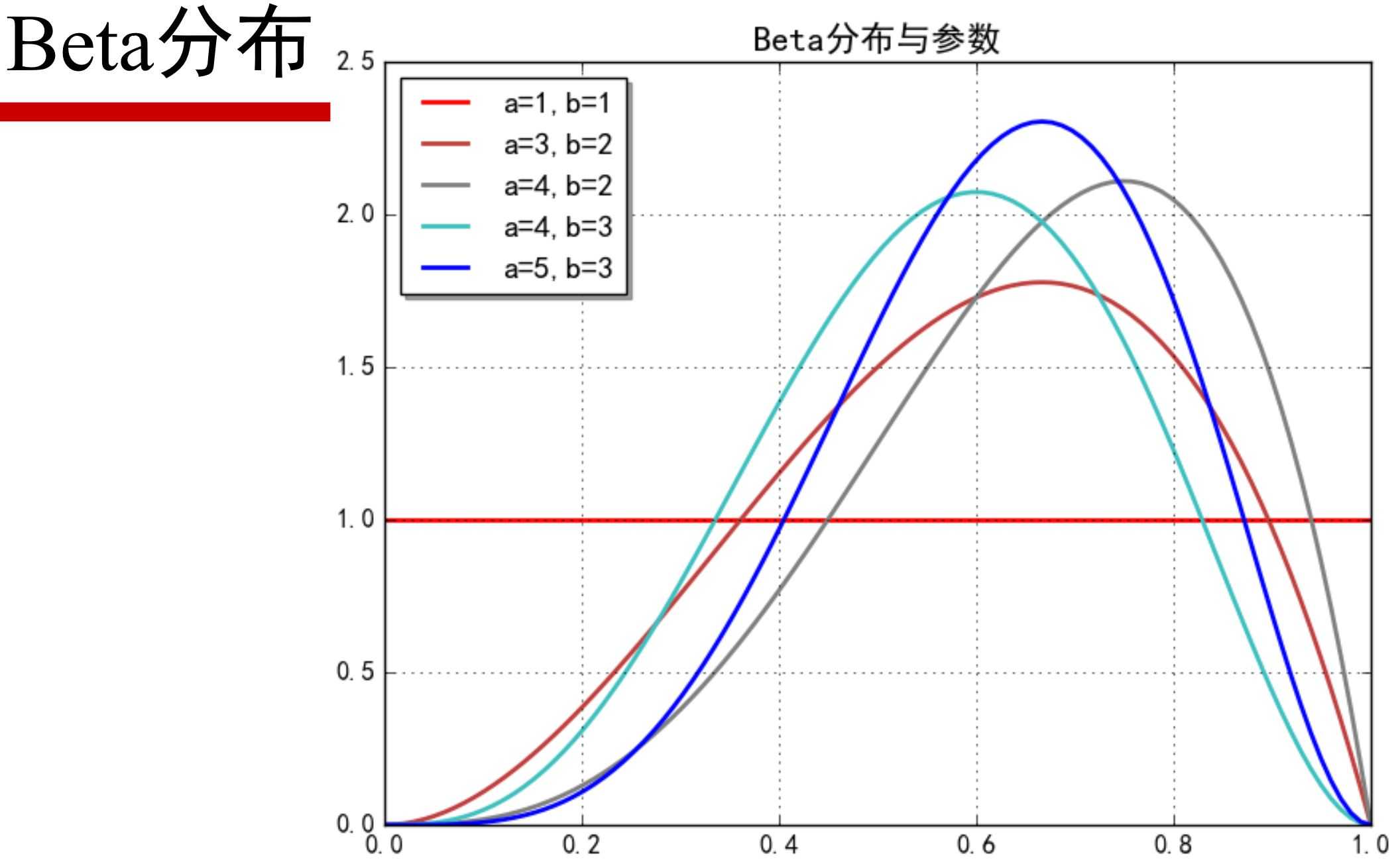
  • 8.Beta分布

    • 
    • 
    • 

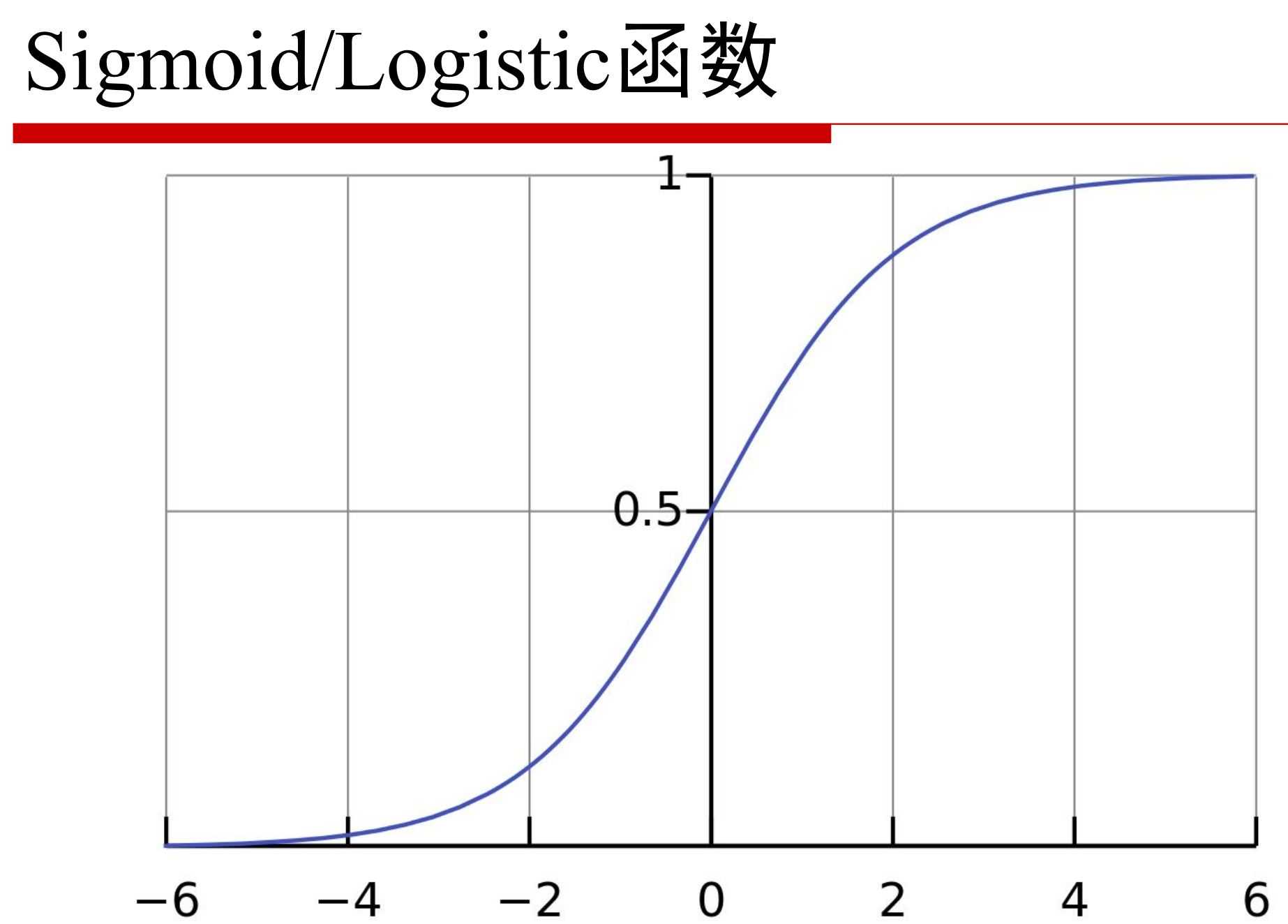
  • 9.指数族分布

    • 
    • 
    • 
    • 

  • 考察参数Φ

    • 
    • 
    • 

2.统计量

• 1.事件独立性

  • 

• 2.期望

  • 即，概率加权下的平均值
  • 离散型：
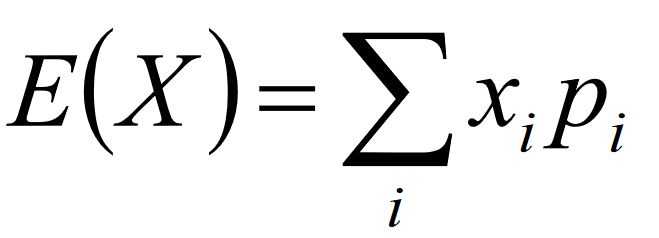
  • 连续型：
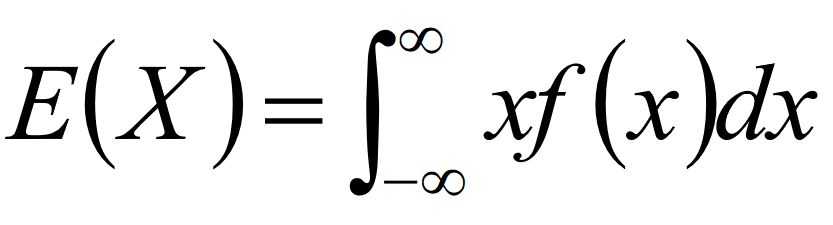
  • 期望的性质：
    • 

  • 例1：计算期望

    
    
    • 
    • 
    • 

  • 例2：集合Hash问题　

    • 
    • 
    • 

• 3.方差

  • 

• 4.协方差

  • 定义：

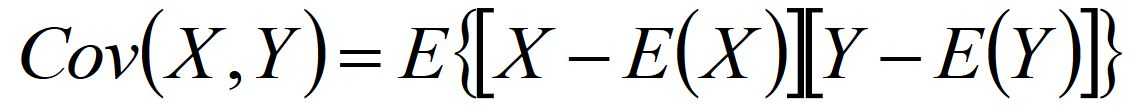
  • 性质：

    • 

  • 协方差和独立、不相关

    • 

  • 协方差的意义

    • 

  • 协方差的上界

    • 

  • 证明过程分析

    • 

  • 协方差上界定理的证明

    • 

  • 再谈独立与不相关

    • 

 

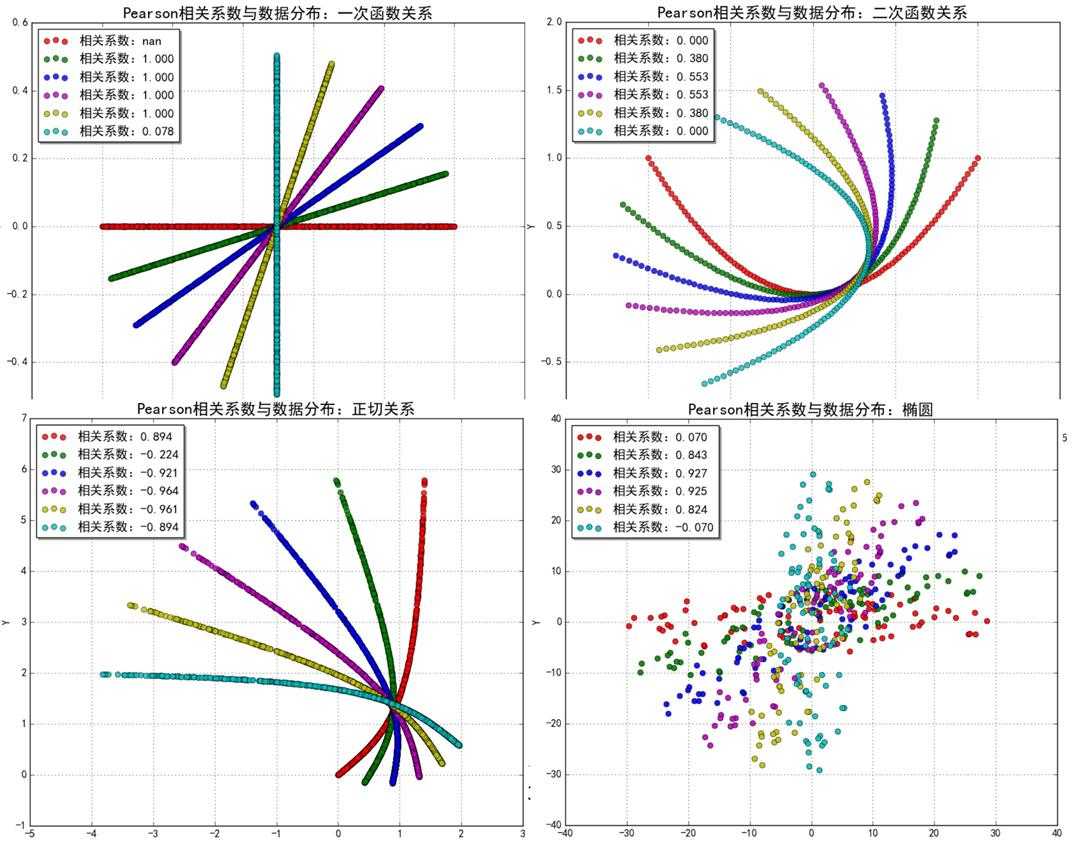
• 5.Pearson相关系数

  • 
  • 

• 6.协方差矩阵

  • 
  • 
  • 

 

3.大数定律

• 1.切比雪夫不等式

  • 

• 2.大数定律

  • 

     

• 3.大数定律的意义

  • 

• 4.重要推论：伯努利定理

  • 
  • 

4.中心极限定理

•  1.中心极限定理

  • 

• 2.例题：标准的中心极限定理的问题

  • 
  • 

• 3.中心极限定理的意义

  • 

• 4.贝叶斯公式带来的思考：

  • 

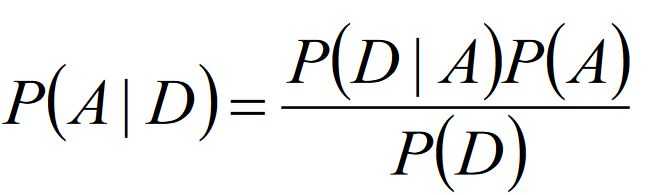
5.最大似然估计

• 1.最大似然估计

  • 

• 2.最大似然估计的具体实践操作

  • 
  • 

• 3.二项分布的最大似然估计

  • 

• 4.正态分布的最大似然估计

  1. 
  2. 
  3. 
  4. 
  5. 
  6. 
• 5. 例题：概率计算
  • 统计某个婚恋网站注册用户的实际年龄，均值25岁，标准差2，试估计用户年龄在21-29岁的概率至少是多少？
  • 

6. 术语摘录