机器学习(10):朴素贝叶斯

Posted 2021-04-25 机器学习研习社

点击“ 机器学习研习社 ”，“置顶”公众号

重磅干货，第一时间送达
回复【大礼包】送你机器学习资料与笔记

回顾

支持向量机

开始学习朴素贝叶斯，先了解一下贝爷，以示敬意。

托马斯·贝叶斯 (Thomas Bayes),英国神学家、数学家、数理统计学家和哲学家，1702年出生于英国伦敦，做过神甫；1742年成为英国皇家学会会员；1763年4月7日逝世。贝叶斯曾是对概率论与统计的早期发展有重大影响的两位（贝叶斯和布莱斯·帕斯卡Blaise Pascal）人物之一。

贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论，并创立了贝叶斯统计理论，对于统计决策函数、统计推断、统计的估算等做出了贡献。1763年发表了这方面的论著，对于现代概率论和数理统计都有很重要的作用。贝叶斯的《An essay towards solving a problem in the doctrine of chances》发表于1758年，贝叶斯所采用的许多术语被沿用至今。贝叶斯对统计推理的主要贡献是使用了"逆概率"这个概念，并把它作为一种普遍的推理方法提出来，即贝叶斯定理。

一、回顾概率统计基础知识

独立事件：在一次实验中，一个事件的发生不会影响到另一事件发生的概率，二者没有任何关系。如果A₁,A₂,A₃…A_n相互独立，则A₁~ A_n同时发生的概率：

 

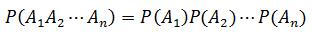
条件概率：指在A事件发生的条件下，事件B发生的概率，用符号表示：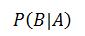

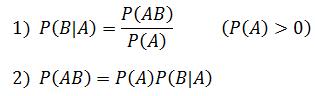
全概率公式：如果事件A1、A2、A3…An 构成一个完备事件组，即它们两两互不相容，其和为全集Ω；并且P(Ai) > 0，则对任一试验B有：

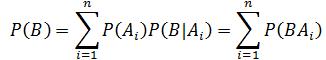
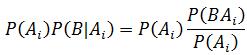
其他概率基础，大家如有兴趣请移步：

二、贝叶斯定理

贝叶斯定理（Bayes’s Rule）：如果有k个互斥且有穷个事件 B1,B2···，Bk，并且，P (B1) + P(B2) + · · · + P(Bk) = 1和一个可以观测到的事件A，那么有：

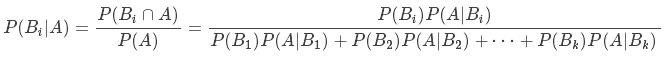
这就是贝叶斯公式，其中：

P(Bi) 为先验概率，即在得到新数据前某一假设的概率;

P(Bi|A) 为后验概率，即在观察到新数据后计算该假设的概率;

P(A|Bi)为似然度，即在该假设下得到这一数据的概率;

P(A)为标准化常量，即在任何假设下得到这一数据的概率。

证明起来也不复杂

1、根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为：

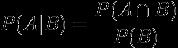
2、同样地，在事件 A 发生的条件下事件 B 发生的概率为：

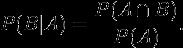
3、结合这两个方程式，我们可以得到：

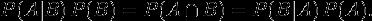
4、上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理:

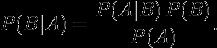
在B出现的前提下，A出现的概率等于A出现的前提下B出现的概率乘以A出现的概率再除以 B 出现的概率。通过联系 A 与 B，计算从一个事件发生的情况下另一事件发生的概率，即从结果上溯到源头（也即逆向概率）。

贝叶斯公式以及由此发展起来的一整套理论与方法，在概率统计中被称为贝叶斯学派，与概率学派有着完全不同思考问题方式。

• 频率学派：研究的是事件本身，所以研究者只能反复试验去逼近它从而得到结果。比如：想要计算抛掷一枚硬币时正面朝上的概率，我们需要不断地抛掷硬币，当抛掷次数趋向无穷时正面朝上的频率即为正面朝上的概率。

• 贝叶斯学派：研究的是观察者对事物的看法，所以你可以用先验知识和收集到的信息去描述他，然后用一些证据去证明它。还是比如抛硬币，当小明知道一枚硬币是均匀的，然后赋予下一次抛出结果是正面或反面都是50%的可信度（概率分布），可能是出于认为均匀硬币最常见这种信念，然后比如小明随机抛了1000次，发现结果正是这样，那么它就通过这些证据验证了自己的先验知识。（也有存在修改的时候，比如发现硬币的材质不一致，总之就是这么一个过程）

举个例子

假设有两个各装了100个球的箱子，甲箱子中有70个红球，30个绿球，乙箱子中有30个红球，70个绿球。假设随机选择其中一个箱子，从中拿出一个球记下球色再放回原箱子，如此重复12次，记录得到8次红球，4次绿球。问题来了，你认为被选择的箱子是甲箱子的概率有多大？

刚开始选择甲乙两箱子的先验概率都是50%，因为是随机二选一（这是贝叶斯定理二选一的特殊形式）。即有：

P(甲) = 0.5， P(乙) = 1 - P(甲)；

这时在拿出一个球是红球的情况下，我们就应该根据这个信息来更新选择的是甲箱子的先验概率：

P(甲|红球1) = P(红球|甲) × P(甲) / (P(红球|甲) × P(甲) + (P(红球|乙) × P(乙)))

P(红球|甲)：甲箱子中拿到红球的概率

P(红球|乙)：乙箱子中拿到红球的概率

因此在出现一个红球的情况下，选择的是甲箱子的先验概率就可被修正为：

P(甲|红球1) = 0.7 × 0.5 / (0.7 × 0.5 + 0.3 × 0.5) = 0.7

即在出现一个红球之后，甲乙箱子被选中的先验概率就被修正为：

P(甲) = 0.7， P(乙) = 1 - P(甲) = 0.3；

如此重复，直到经历8次红球修正（概率增加），4此绿球修正（概率减少）之后，选择的是甲箱子的概率为：96.7%。

Python 代码来解这个问题：

def bayesFunc(pIsBox1, pBox1, pBox2):
return (pIsBox1 * pBox1)/((pIsBox1 * pBox1) + (1 - pIsBox1) * pBox2)
def redGreenBallProblem():
pIsBox1 = 0.5
# consider 8 red ball
for i in range(1, 9):
pIsBox1 = bayesFunc(pIsBox1, 0.7, 0.3)
print " After red %d > in 甲 box: %f" % (i, pIsBox1)
# consider 4 green ball
for i in range(1, 5):
pIsBox1 = bayesFunc(pIsBox1, 0.3, 0.7)
print " After green %d > in 甲 box: %f" % (i, pIsBox1)
redGreenBallProblem()

运行结果如下：

After red 1 > in 甲 box: 0.700000
After red 2 > in 甲 box: 0.844828
After red 3 > in 甲 box: 0.927027
After red 4 > in 甲 box: 0.967365
After red 5 > in 甲 box: 0.985748
After red 6 > in 甲 box: 0.993842
After red 7 > in 甲 box: 0.997351
After red 8 > in 甲 box: 0.998863
After green 1 > in 甲 box: 0.997351
After green 2 > in 甲 box: 0.993842
After green 3 > in 甲 box: 0.985748
After green 4 > in 甲 box: 0.967365

很明显可以看到红球的出现是增加选择甲箱子的概率，而绿球则相反。

三、朴素贝叶斯算法

朴素贝叶斯（Naive Bayesian）是基于贝叶斯定理和特征条件独立假设的分类方法，它通过特征计算分类的概率，选取概率大的情况进行分类，因此它是基于概率论的一种机器学习分类方法。因为分类的目标是确定的，所以也是属于监督学习。朴素贝叶斯假设各个特征之间相互独立，所以称为朴素。它简单、易于操作，基于特征独立性假设，假设各个特征不会相互影响，这样就大大减小了计算概率的难度。

1.  朴素贝叶斯算法的执行流程如下:

1)设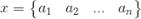为待分类项,其中a为x的一个特征属性

2)类别集合为: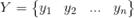

3)根据贝叶斯公式,计算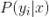

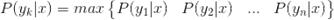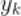 4)如果 ,则x属于这一类.

2.  高斯朴素贝叶斯(一般使用在特征属性连续的情况下)

    上面的算法流程中可以看出,朴素贝叶斯算法就是对贝叶斯公式的一种运用,它没有进行任何的改变.

    在计算条件概率时,对于离散的数据特征可以使用大数定理(频率代替概率的思想).但是,怎么处理连续的特征呢?这里我们一般使用高斯朴素贝叶斯.

   所谓高斯朴素贝叶斯,就是当特征属性为连续值并且服从高斯分布时,可以使用高斯分布的概率公式直接计算条件概率的值。

    

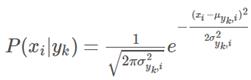
    此时,我们只需要计算各个类别下的特征划分的均值和标准差.

3.  多项式朴素贝叶斯(一般使用在特征属性离散的情况下)

    所谓多项式朴素贝叶斯,就是特征属性服从多项式分布,进而对于每一个类别y,参数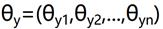，其中n为特征属性数目，那么P(xi|y)的概率为θyi。

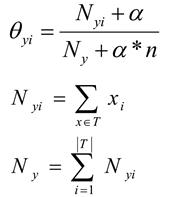
4.  伯努利朴素贝叶斯(一般使用在缺失值较多的情况下)

    与多项式模型一样，伯努利模型适用于离散特征的情况，所不同的是，伯努利模型中每个特征的取值只能是1和0(以文本分类为例，某个单词在文档中出现过，则其特征值为1，否则为0).

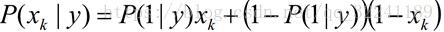
四、朴素贝叶斯实战

sklearn中有3种不同类型的朴素贝叶斯：

高斯分布型：用于classification问题，假定属性/特征服从正态分布的。

多项式型：用于离散值模型里。比如文本分类问题里面我们提到过，我们不光看词语是否在文本中出现，也得看出现次数。如果总词数为n，出现词数为m的话，有点像掷骰子n次出现m次这个词的场景。

伯努利型：最后得到的特征只有0(没出现)和1(出现过)。

例1 我们使用iris数据集进行分类

from sklearn.naive_bayes import GaussianNB
from sklearn.model_selection import cross_val_score
from sklearn import datasets
iris = datasets.load_iris()
gnb = GaussianNB()
scores=cross_val_score(gnb, iris.data, iris.target, cv=10)
print("Accuracy:%.3f"%scores.mean())

输出: Accuracy:0.953

例2 Kaggle比赛之“旧金山犯罪分类预测”

(1) 首先我们来看一下数据

import pandas as pd  
import numpy as np  
from sklearn import preprocessing  
from sklearn.metrics import log_loss  
from sklearn.cross_validation import train_test_split
train = pd.read_csv('/Users/liuming/projects/Python/ML数据/Kaggle旧金山犯罪类型分类/train.csv', parse_dates = ['Dates'])  
test = pd.read_csv('/Users/liuming/projects/Python/ML数据/Kaggle旧金山犯罪类型分类/test.csv', parse_dates = ['Dates'])  
train  

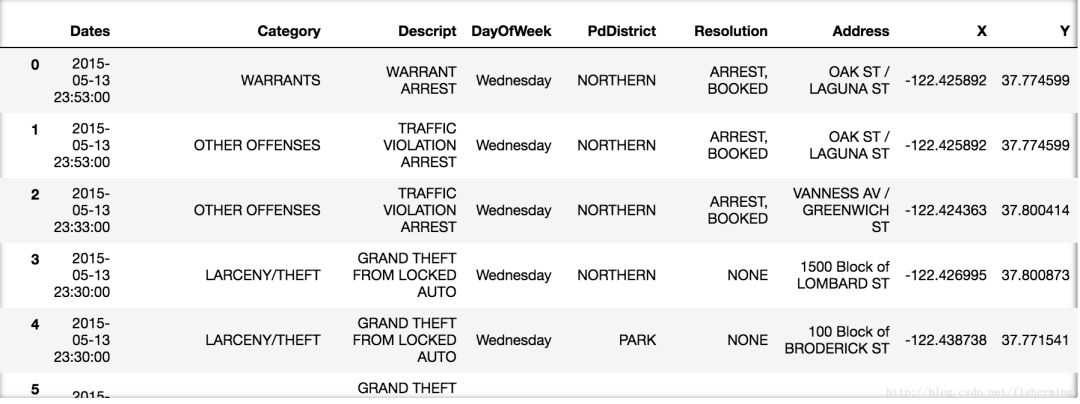
我们依次解释一下每一列的含义：

Date: 日期
Category: 犯罪类型，比如 Larceny/盗窃罪 等.
Descript: 对于犯罪更详细的描述
DayOfWeek: 星期几
PdDistrict: 所属警区
Resolution: 处理结果，比如说『逮捕』『逃了』
Address: 发生街区位置
X and Y: GPS坐标
train.csv中的数据时间跨度为12年，包含了将近90w的记录。另外，这部分数据，大家从上图上也可以看出来，大部分都是『类别』型，比如犯罪类型，比如星期几。
（2）特征预处理
sklearn.preprocessing模块中的 LabelEncoder函数可以对类别做编号，我们用它对犯罪类型做编号；pandas中的get_dummies( )可以将变量进行二值化01向量，我们用它对”街区“、”星期几“、”时间点“进行因子化。

#对犯罪类别:Category; 用LabelEncoder进行编号  
leCrime = preprocessing.LabelEncoder()  
crime = leCrime.fit_transform(train.Category)   #39种犯罪类型  
#用get_dummies因子化星期几、街区、小时等特征  
days=pd.get_dummies(train.DayOfWeek)  
district = pd.get_dummies(train.PdDistrict)  
hour = train.Dates.dt.hour  
hour = pd.get_dummies(hour)  
#组合特征  
trainData = pd.concat([hour, days, district], axis = 1)  #将特征进行横向组合  
trainData['crime'] = crime   #追加'crime'列  
days = pd.get_dummies(test.DayOfWeek)  
district = pd.get_dummies(test.PdDistrict)  
hour = test.Dates.dt.hour  
hour = pd.get_dummies(hour)  
testData = pd.concat([hour, days, district], axis=1)  
trainData 

特征预处理后，训练集feature，如下图所示：

(3) 建模

from sklearn.naive_bayes import BernoulliNB
import time
features=['Monday', 'Tuesday', 'Wednesday', 'Thursday', 'Friday', 'Saturday', 'Sunday', 'BAYVIEW', 'CENTRAL', 'INGLESIDE', 'MISSION',  
 'NORTHERN', 'PARK', 'RICHMOND', 'SOUTHERN', 'TARAVAL', 'TENDERLOIN']  
X_train, X_test, y_train, y_test = train_test_split(trainData[features], trainData['crime'], train_size=0.6)  
NB = BernoulliNB()  
nbStart = time.time()  
NB.fit(X_train, y_train)  
nbCostTime = time.time() - nbStart  
#print(X_test.shape)  
propa = NB.predict_proba(X_test)   #X_test为263415*17；那么该行就是将263415分到39种犯罪类型中，每个样本被分到每一种的概率  
print("朴素贝叶斯建模%.2f秒"%(nbCostTime))  
predicted = np.array(propa)  
logLoss=log_loss(y_test, predicted)  
print("朴素贝叶斯的log损失为:%.6f"%logLoss)  

输出：
朴素贝叶斯建模0.55秒
朴素贝叶斯的log损失为:2.582561

例3 文本分类——垃圾邮件过滤

收集数据：提供文本文件
准备数据：将文本文件解析成词条向量
分析数据；检查词条确保解析的正确性
训练算法：使用之前建立的trainNB0()函数
测试算法：使用classifyNB()，并且构建一个新的测试函数来计算文档集的错误率
使用算法：构建一个完整的程序对一组文档进行分类，将错分的文档输出到屏幕上

准备数据：切分文本

使用正则表达式切分，其中分隔符是除单词、数字外的任意字符

import re
mySent = 'This book is the best book on Python or M.L. I have ever laid eyes upon.'
regEx = re.compile('\\W*')
listOfTokens = regEx.split(mySent)
# 去掉长度小于0的单词，并转换为小写
[tok.lower() for tok in listOfTokens if len(tok) > 0]
[out]
['this', 'book', 'is', 'the', 'best', 'book', 'on', 'python', 'or', 'm', 'l', 'i', 'have', 'ever', 'laid', 'eyes', 'upon']

切分邮件

emailText = open('email/ham/6.txt').read()
listOfTokens = regEx.split(emailText)

测试算法：使用朴素贝叶斯进行交叉验证

import randomdef textParse(bigString):
    '''
    字符串解析
    '''
    import re    # 根据非数字字母的任意字符进行拆分
    listOfTokens = re.split(r'\W*', bigString)    # 拆分后字符串长度大于2的字符串，并转换为小写
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]def spamTest():
    '''
    贝叶斯分类器对垃圾邮件进行自动化处理
    '''
    docList = []
    classList = []
    fullText = []    for i in range(1, 26):        # 读取spam文件夹下的文件，并转换为特征和标签向量
        wordList = textParse(open('email/spam/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(1)        # 读取ham文件夹下的文件，并转换为特征和标签向量
        wordList = textParse(open('email/ham/%d.txt' % i).read())
        docList.append(wordList)
        fullText.extend(wordList)
        classList.append(0)    # 转换为词列表
    vocabList = createVocabList(docList)    # 初始化训练集和测试集
    trainingSet = range(50);
    testSet = []    # 随机抽取测试集索引
    for i in range(10):
        randIndex = int(random.uniform(0, len(trainingSet)))
        testSet.append(trainingSet[randIndex])        del(trainingSet[randIndex])

    trainMat = []
    trainClasses = []    # 构造训练集
    for docIndex in trainingSet:
        trainMat.append(setOfWords2Vec(vocabList, docList[docIndex]))
        trainClasses.append(classList[docIndex])    # 朴素贝叶斯分类模型训练
    p0V, p1V, pSpam = trainNB0(np.array(trainMat), np.array(trainClasses))
    errorCount = 0

    # 朴素贝叶斯分类模型测试
    for docIndex in testSet:
        wordVector = setOfWords2Vec(vocabList, docList[docIndex])        if classifyNB(np.array(wordVector), p0V, p1V, pSpam) != classList[docIndex]:
            errorCount += 1
            print 'classification error', docList[docIndex]    print 'the error rate is: ',float(errorCount)/len(testSet)

由于SpamTest()构造的测试集和训练集是随机的，所以每次运行的分类结果可能不一样。如果发生错误，函数会输出错分文档的词表，这样就可以了解到底哪篇文档发生了错误。这里出现的错误是将垃圾邮件误判为了正常邮件。

import randomdef textParse(bigString):
    '''
    字符串解析
    '''
    import re    # 根据非数字字母的任意字符进行拆分
    listOfTokens = re.split(r'\W*', bigString)    # 拆分后字符串长度大于2的字符串，并转换为小写
    return [tok.lower() for tok in listOfTokens if len(tok) > 2]def spamTest():
    '''
    贝叶斯分类器对垃圾邮件进行自动化处理
    '''
spamTest()
[out]
classification error ['benoit', 'mandelbrot', '1924', '2010', 'benoit', 'mandelbrot', '1924', '2010', 'wilmott', 'team', 'benoit', 'mandelbrot', 'the', 'mathematician', 'the', 'father', 'fractal', 'mathematics', 'and', 'advocate', 'more', 'sophisticated', 'modelling', 'quantitative', 'finance', 'died', '14th', 'october', '2010', 'aged', 'wilmott', 'magazine', 'has', 'often', 'featured', 'mandelbrot', 'his', 'ideas', 'and', 'the', 'work', 'others', 'inspired', 'his', 'fundamental', 'insights', 'you', 'must', 'logged', 'view', 'these', 'articles', 'from', 'past', 'issues', 'wilmott', 'magazine']
the error rate is:  0.1spamTest()
[out]
the error rate is:  0.0

参考文献：

https://blog.csdn.net/fisherming/article/details/79509025

https://blog.csdn.net/qq_32241189/article/details/80194653

http://blog.csdn.net/kesalin/article/details/40370325

相关阅读：

支持向量机

机器学习研习社：目前是由国内985博士，硕士组成的团体发起并运营。主要分享和研究机器学习、深度学习、NLP 、Python，大数据等前沿知识、干货笔记和优质资源。