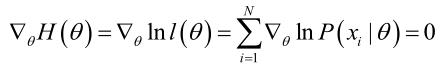机器学习——朴素贝叶斯算法

Posted 2022-12-15 摆脱咸鱼

机器学习——朴素贝叶斯算法

• • 贝叶斯定理
  • • 正向概率和逆向概率
    • 条件概率与全概率
    • 贝叶斯公式推导
  • 极大似然估计
  • 朴素贝叶斯分类器
  • • 朴素
    • 可能性函数的作用
    • 拉普拉斯修正
    • 防溢出策略
    • 样例解释
  • 代码——使用拉普拉斯进行垃圾邮件分类
  • • 构建文本向量
    • 从词向量到计算概率
    • 朴素贝叶斯分类器分类函数
    • 垃圾邮件分类
  • 总结

朴素贝叶斯是有监督学习的一种分类算法，它基于“贝叶斯定理”实现，故在学习“朴素贝叶斯算法”前，有必要先了解“贝叶斯定理”。

贝叶斯定理

定义：贝叶斯算法是在概率框架下实施决策的基本方法，对分类任务来说，在所有相关概率都已知的理想情形下，贝叶斯算法考虑的是如何基于这些概率和误判损失来选择最优的类别标记。

目的：解决“逆向概率问题”

贝叶斯公式：
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$

P(A) ：概率中最基本的符号，表示 A 出现的概率。例：在投掷骰子时，P(2) 指的是骰子出现数字“2”的概率，这个概率是 1/6。

P(B|A)： 条件概率的符号，表示事件 A 发生的条件下，事件 B 发生的概率，条件概率是“贝叶斯公式”的关键所在，它也被称为“似然度”。

P(A|B) ：条件概率的符号，表示事件 B 发生的条件下，事件 A 发生的概率，这个计算结果也被称为“后验概率”。

优缺点：

优点： 稳定的分类效率、对缺失数据不敏感、算法简单、分类精确度高、速度快。

缺点：对训练数据依赖性强、需要知道先验概率（基于假设或者已有训练集训练所得）

正向概率和逆向概率

下面用两个例子说明正向概率和逆向概率的区别

正向概率：假设袋子又N个白球、M个黑球，求从中摸出黑球的概率。

逆向概率：不知道袋子中黑白球比例，从中摸出一个（或几个）球，观察去除球的颜色，由此推测袋子中黑白球的比例。

条件概率与全概率

条件概率定义：指在事件B发生的情况下，事件A发生的概率。

公式：
$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

图示入下：

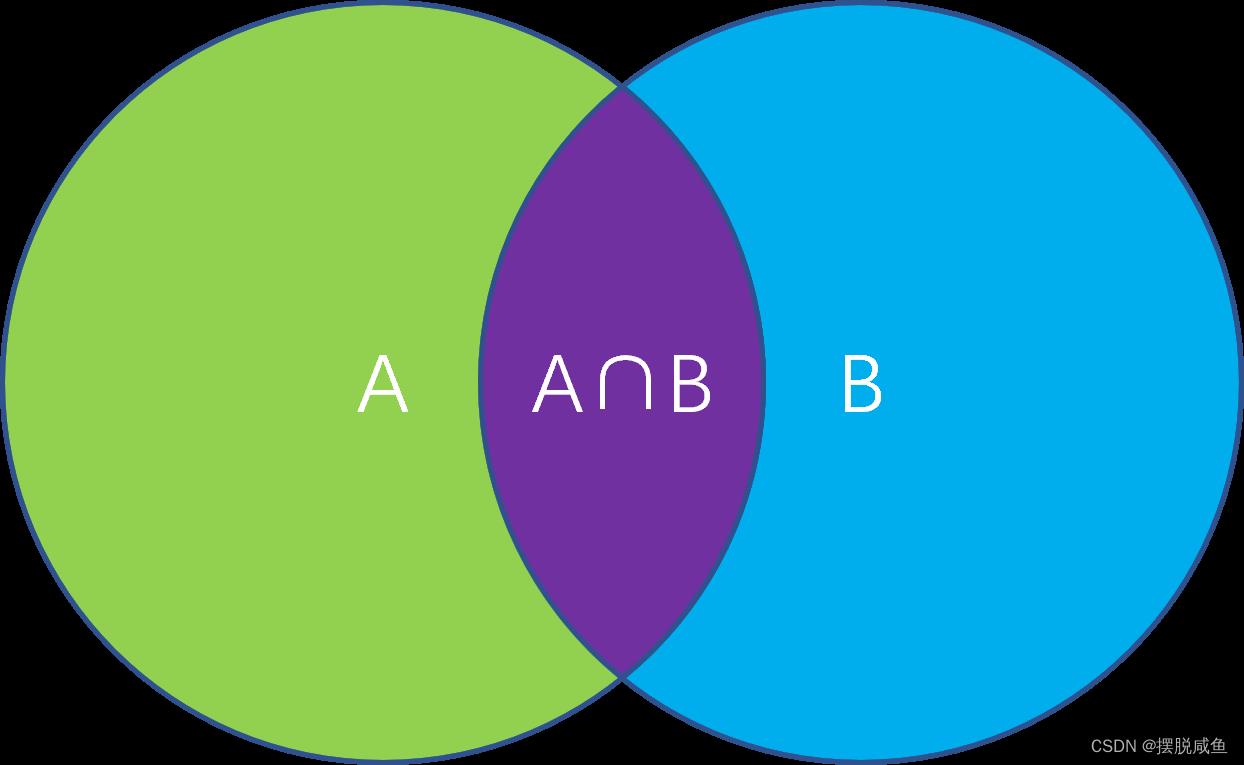
这里的条件概率就是图示中紫色部分占蓝色部分+紫色部分的大小。

全概率定义：如果事件A1、A2（这里仅用两个表示）构成一个完备事件组，即它们两两互不相容，其和为全集；并且P（Ai)大于0，则对任一事件B有：
$$P(B)=P(B|A_1)P(A_1)+P(B|A_2)P(A_2)$$

贝叶斯公式推导

通过上述信息相信你对条件概率已经有了一定的了解，那么接下来咋们就来推导一下贝叶斯公式吧。

首先我们回顾一下贝叶斯公式：
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
根据我们上述所讲的条件概率可知：
$$P(A|B)=\frac{P(A\cap B)}{P(B)}$$

$$P(B|A)=\frac{P(B\cap A)}{P(A)}$$

由我们概率论所学（高中的概率与统计也有涉及）：
$$P(B\cap A)=P(A\cap B)$$
所以有：
$$P(A|B)P(B)=P(A)P(B|A)$$
根据换项可知：
$$P(A|B)=\frac{P(B|A)P(A)}{P(B)}$$
得证。

极大似然估计

原理：利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！

求解过程：

求解极大似然函数：

ML估计：求使得出现该组样本的概率最大的θ值。
$$\hat{\theta }=arg\underset{\theta }{\max }\prod _{i=1}^{N}p(x_i|\theta )$$
实际中为了便于分析，定义了对数似然函数：
$$H(\theta )={\ln }_{}l(\theta )$$

$$\hat{\theta }=arg\underset{\theta }{\max }H(\theta )=arg\underset{\theta }{\max }\sum _{i=1}^N{\ln }_{}p(x_i|\theta )$$

未知参数只有一个（θ为标量）的情况。在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解：

未知参数有多个（θ为向量）则θ可表示为具有S个分量的未知向量：

记梯度算子：

若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。

方程的解只是一个估计值，只有在样本数趋于无限多的时候，它才会接近于真实值。

朴素贝叶斯分类器

定义：朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的输出 Y。

朴素贝叶斯的基础假设：

①每个特征相互独立；
②每个特征的权重（或重要性）都相等，即对结果的影响程度都相同。

由朴素贝叶斯算法可得：
$$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)}$$

P(Y)称为”先验概率”：即在B事件发生之前，我们对A事件概率的一个判断。

P(Y|X)称为”后验概率”：在B事件发生之后，我们对A事件概率的重新评估。

P(X|Y)/P(X)称为”可能性函数”：这是一个调整因子，使得预估概率更接近真实概率。

所以可以得到以下结论：

后验概率=先验概率∗调整因子（可能性函数）

朴素贝叶斯基于各特征之间相互独立，在给定类别为y的情况下，上式可以进一步表示为下式：
$$P(X|Y=y)=\prod _{i=1}^{d}P(x_i|Y=y)$$

由以上两式可以计算出后验概率为：
$$P_{post}=P(Y|X)=\frac{P(Y){\prod }_{i=1}^{d}P(x_i|Y)}{P(X)}$$
即：
P ( Y ∣ X ) = P ( x 1 ∣ Y ) P ( x 2 ∣ Y ) P (