数据结构之二叉树

Posted 2021-03-26 xingxyx

1、二叉树的基本概念

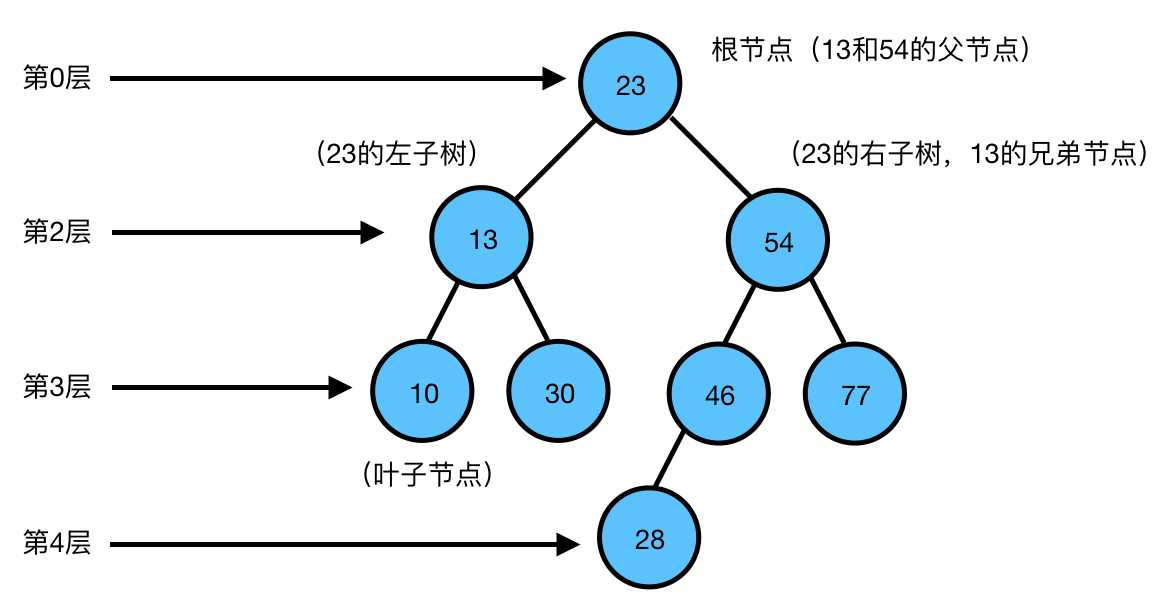
二叉树：二叉树是每个节点最多有两个子树的树结构。

根节点：一棵树最上面的节点称为根节点。

父节点、子节点：如果一个节点下面连接多个节点，那么该节点称为父节点，它下面的节点称为子 节点。

叶子节点：没有任何子节点的节点称为叶子节点。

兄弟节点：具有相同父节点的节点互称为兄弟节点。

节点度：节点拥有的子树数。上图中，13的度为2，46的度为1，28的度为0。

树的深度：从根节点开始（其深度为0）自顶向下逐层累加的。上图中，13的深度是1，30的深度是2，28的深度是3。

树的高度：从叶子节点开始（其高度为0）自底向上逐层累加的。54的高度是2，根节点23的高度是3。

对于树中相同深度的每个节点来说，它们的高度不一定相同，这取决于每个节点下面的叶子节点的深度。上图中，13和54的深度都是1，但是13的高度是1，54的高度是2。

2、二叉树的类型

（1）满二叉树

除最后一层无任何子节点外，每一层上的所有节点都有两个子节点，最后一层都是叶子节点。满足下列性质：

1）一颗树深度为h，最大层数为k，深度与最大层数相同，k=h；

2）叶子节点数（最后一层）为2^k−1；

3）第 i 层的节点数是：2ⁱ⁻¹；

4）总节点数是：2^k−1，且总节点数一定是奇数。

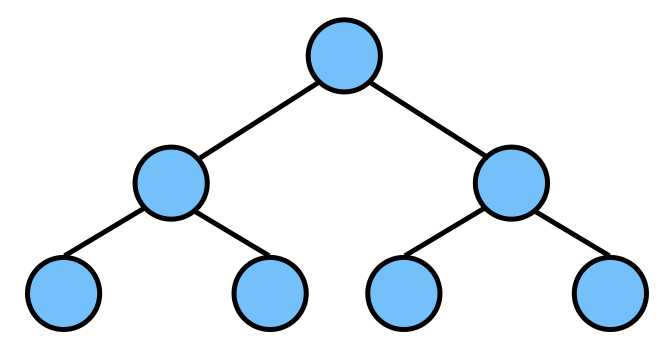
（2） 完全二叉树

若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。满足下列性质：

1）只允许最后一层有空缺结点且空缺在右边，即叶子节点只能在层次最大的两层上出现；

2）对任一节点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个；

3）除最后一层，第 i 层的节点数是：2ⁱ⁻¹；

4）有n个节点的完全二叉树，其深度为：log²ⁿ⁺¹或为log²ⁿ⁺¹；

5）满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树。

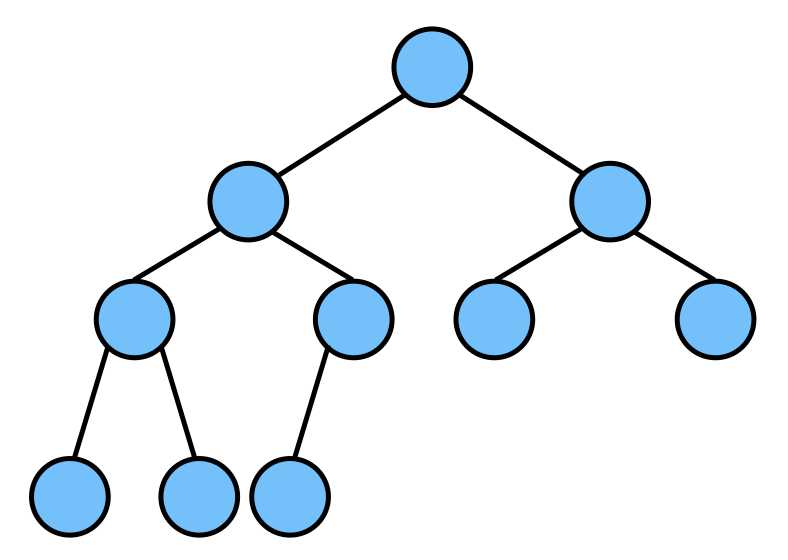
 （3）平衡二叉树

 

 

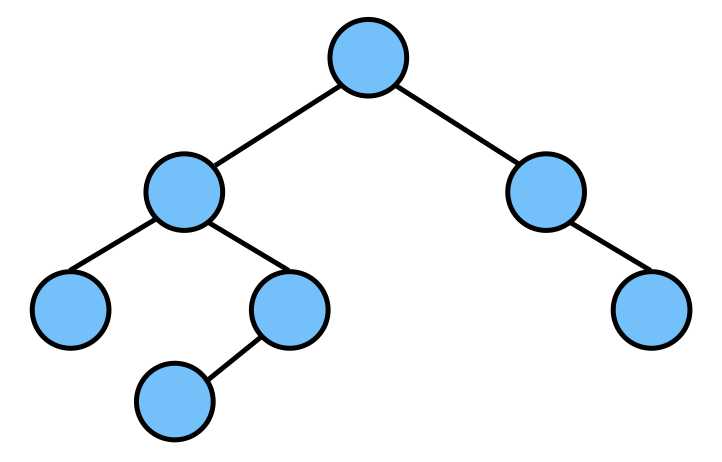
 又被称为AVL树，它是一颗空树或左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

（4）二叉搜索树

又称二叉查找树、二叉排序树（Binary Sort Tree）。它是一颗空树或是满足下列性质的二叉树：

1）若左子树不空，则左子树上所有节点的值均小于或等于它的根节点的值；

2）若右子树不空，则右子树上所有节点的值均大于或等于它的根节点的值；

3）左、右子树也分别为二叉排序树。

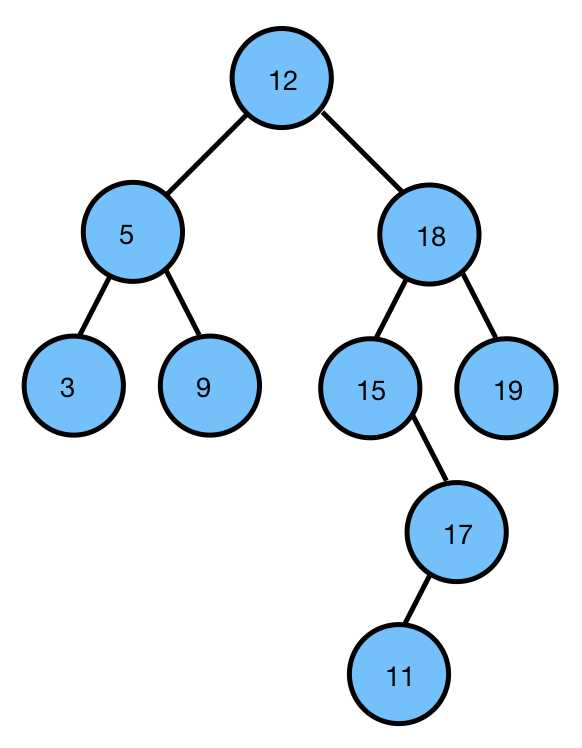
3、二叉树的遍历

 

 

先序遍历：中、左、右

中序遍历：左、中、右

后序遍历：左、右、中